前言

昨天說完Autoencoder與GAN的聯繫後，今天就來說說GAN的相關數學吧！這邊我會簡單介紹GAN其數學原理，那我們廢話不多說，正文開始！

正文

在原始論文中，作者將生成器想像成一組偽幣製造者，試圖製造偽幣並在不被檢測到的情況下使用它們，而鑑別器則類似於警察，試圖檢測偽幣。在這個遊戲中的競爭驅使兩個模型不斷改進他們的方法，直到偽幣與真品難以區分。

GAN包括兩個主要部分：

1. 生成器（Generator），表示為 G：它接收一些隨機噪聲 z 並生成假數據 x。
2. 鑑別器（Discriminator），表示為 D：它試圖區分真實數據（x 來自訓練數據集）和生成器生成的假數據。

GAN的目標是訓練這兩個部分，使生成器能夠生成與真實數據相似的數據，而鑑別器則無法區分真實和假數據。

GAN的數學概念是通過以下最小最大博弈來表示：

1. 生成器的目標是最小化生成的假數據被鑑別器認為是假的概率：

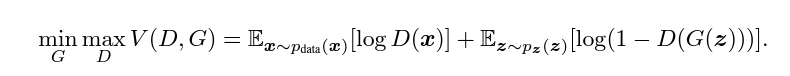
這意味著生成器 G 試圖生成能夠愚弄鑑別器 D 的假數據，同時鑑別器 D 試圖區分真實和假數據。當 G 和 D 都達到平衡時，生成器可以生成逼真的數據。

生成器與鑑別器的訓練目標

生成器目標：

更新生成器（Generator）的權重（θg）使鑑別器難以區分生成的假數據

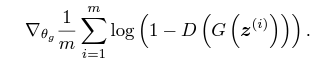
鑑別器目標：

鑑別器 D 的目標是最大化正確區分真實和假數據的能力：

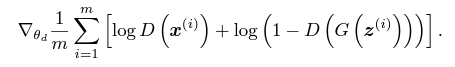
這表示鑑別器試圖區分真實數據x^i和生成器生成G(x^i)的假數據。

這兩個網路相互對抗，通過交替優化，生成器學習生成更逼真的數據，同時鑑別器學習更好地區分真假數據，直到達到訓練要求的次數

詳情可以看論文：論文

總結

以上就是今天關於生成對抗網路的簡單介紹啦，明天將會實作簡單的GAN，那我們明天見！