當我們要評估一名運動員的好壞,就會針對一些體能項目做評估,像是肌耐力、爆發力、彈跳力等,這些項目也可以稱做是衡量球員水準的指標,同樣的如果我們要評估一個模型的好壞,就會需要用一些指標來當作衡量的基準,這些指標就叫作模型的驗證指標 ( Validation index ),這些指標包含了較常見的準確率、錯誤率、精確率、召回率、F1 分數,昨天介紹過了混淆矩陣的中一些重要參數 ( TN、FN、TP、FP ),今天就要來用這些參數來計算出每個指標啦。
我們沿用昨天的二元混淆矩陣當作例子來計算指標:
圖 ( 一 )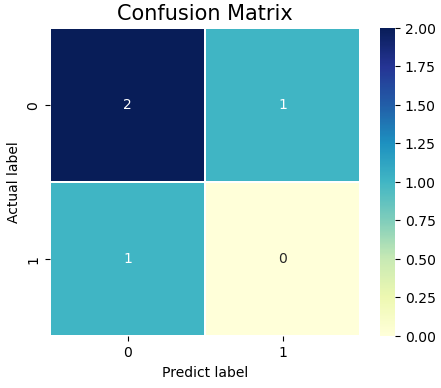
在醫學上,一個高準確率的醫學預測模型,能夠精準檢測出全部患者的病情 ( 陽性 1 或陰性 0 ),要求出準確率,就要知道全部真實資料 ( 全部患者 ) 的數量有多少來當作分母,就圖( 一 ) 來說,昨天我們知道第一列的總合 ( TN + FP ) 和第二列的總和 ( FN + TP ) 分別代表真實資料為 0 ( 陰性患者 ) 和真實資料為 1 ( 陽性患者 ) 的數量,所以我們只要把這兩列的總和加起來就會是全部真實資料 ( 全部患者 = 陰性患者 + 陽性患者 ) 的數量,因此得到 ( TN + FP ) + ( FN + TP ) 做為準確率分母,至於分子就會是預測正確 ( 陽性患者被檢測為陽性,陰性患者被檢測為陰性 ) 的數量,也就是 TN + TP,所以最後準確率的計算方式就是:
用前面準確率的概念,分母也是用全部真實資料 ( 全部患者 ) 的數量,但分子要放預測錯誤的數量,也就是 FN + FP,所以得出錯誤率公式:
精確率也稱查準率,就是檢查正確檢測出陽性的比率,就圖( 一 ) 來說,精確度就是針對在預測為 1 時 ( 所有的檢測中 ),預測為 1 時真實值也為 1 ( 檢測為陽性患者實際也陽性 ) 的比率 ,也可說是計算當預測為 1 ( 檢測為陽性 ) 時的準確率,那既然是求準確率就要先求出分母,就是預測為 1 的總數,也就是 TP + FP,分子再放預測為1 正確的數量,也就是 TP,因此得到精確率計算公式:
在醫學中,一個高精確率的醫學檢測模型可以確保當檢測患者為陽性時 ( 預測為 1 ),患者也的確為陽性 ( 真實為 1 ) 的數量 ( TP ) 高,也就是模型檢測為陽性時,患者其實是陰性 ( FP ) 的數量較低,這能夠大大減少患者因為誤判為陽性所花費的治療費用等不必要的醫療成本,高的精確率也可說是保證了模型預測為陽性時的準確度。
召回率就是敏感度 ( Sensitivity )、真陽率 ( True Positive Rate , TPR ) 或查全率,在醫學上,就是檢查所有陽性患者被檢測出陽性的比率,就圖( 一 ) 來說,召回率就是針對在真實值為 1 時 ( 所有的陽性患者 ),預測也為 1 的比率 ( 檢測出陽性 ),那就要先求出比率的分母,就是真實值為 1 的總數,前面提過就是矩陣第二列的總和 ( FP + TP ),分子的部分就放預測為 1 正確的數量,因此得到召回率計算公式:
在醫學上,召回率高的模型在患者為陽性時較容易被正確的檢測 ( 預測 ),能夠減少偽陰性 ( FN ) 的情況發生,高偽陰性是非常具有風險的,患者可能實際上為陽性 ( 真實值為1 ),但因為高偽陰性的關係會檢測不出患者有陽性而檢測出陰性 ( 預測為 0 ),患者可能會因此錯過黃金的治療時間,所以對於一個醫學檢測模型,高召回率意味著能夠越準確的檢測到患者陽性的症狀,即使有時候患者沒有陽性卻檢測出陽性,但這總比實際為陽性卻沒檢測出來好,因為患者可能就會因此有警覺心而跑去別的地方問診確認,從而避免誤判的情形,高的召回率也可說是保證了實際為陽性患者,較容易被模型檢測出為陽性的能力。
但值得注意的是,精確率和召回率之間是存在權衡關係的,高的召回率,患者就會太容易被檢測出陽性,這樣反倒會讓檢測為陽性時的準確率下降,因為其實有些被檢測為陽性的患者實際上根本不是陽性,在召回率上升的同時也讓精確率逐漸下降,而高的精確率代表更加保守的預測患者為陽性,陽性的患者可能會因預測的過度保守而沒被檢測出陽性,因此降低召回率,所以必須要根據實際的需求來權衡兩個指標之間的大小。
剛才提到的精確率和召回率之間的權衡,可以用 F1 分數當指標做評估,F1 分數的計算公式為:
F1 分數相當於把精確率和召回率結合起來做兩者間的平衡,越高的 F1 分數表示在兩個指標之間取得較好的平衡,讓模型能在平衡精確率和召回率的情況下有較好的效能表現。
今天我們學到如何利用混淆矩陣所得到的資訊計算出驗證指標,包括:準確率、錯誤率、精確率、召回率、F1 分數,我們就可以用這些參數來評估模型的效能,明天我們要繼續介紹其它的評估方法,也就是 ROC / AUC 特性曲線,通過這個曲線便可清楚的知道模型的好壞,那我們下篇文章見 ~
