我們在上一篇已經提到說，我們要找的東西實際上是一個機率，如果這個 Posterior probability > 0.5 的話，就 output C1，否則就 output C2。

找一個Function set

假設如果要找的東西是一個Gaussian Distribution的話，我們可以用sigma(z)表示，而這個z就會是 w 跟 x 的 inner product 加上 b：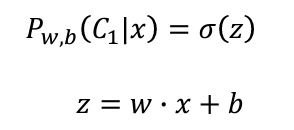

sigma(z)（這裏使用sigmoid函數）公式：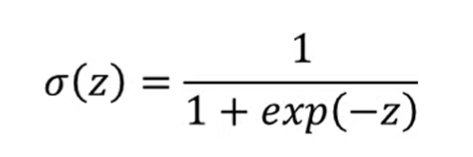

所以最後我們的function set會是這樣的：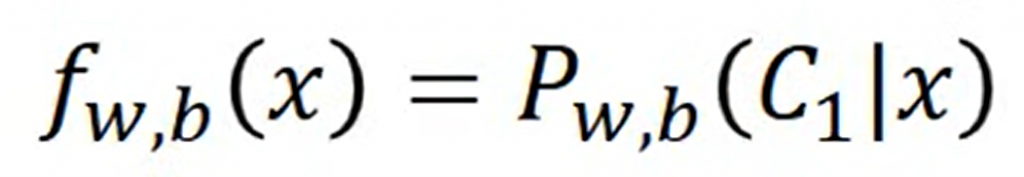

這邊的f下標w和b表示的是，我們這個function set是受w和b所控制的，就像我們之前説到機器學習的三個步驟一樣，第一步就是找到一個function set，而現在我們找到的就是這樣一個綫性的function set，輸入一個x，給出它屬於Class 1 的機率。

如果我們用圖像來表示整個流程的話：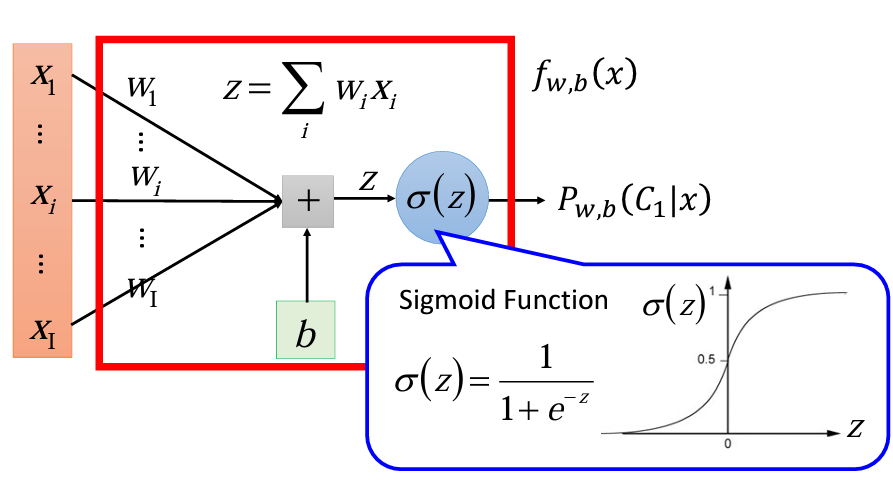

可以看到我們的最左邊的輸入是一個X的vector，裏面每個dimension都有一個對應的w組成的W的vector，再加上一個b，這整個的summation就是z，丟進一個sigma激活函數（這邊用sigmoid，但也可以是softmax、ReLu等），output就是這個丟進去的x屬於class 1 的機率。

衡量Function set的好壞

假設我們現在有一組資料，標好每個x屬於哪個class：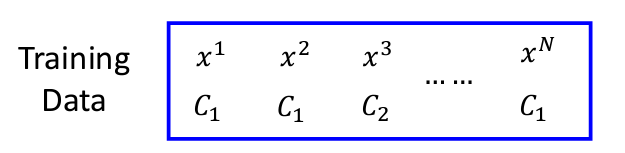

那麽我們現在要做的就是找出最大的似然（Likelihood），公式如下：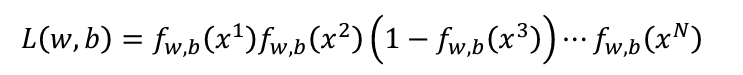

這裏的L指的不是Loss Function，而是Likelihood。另外一個需要注意的是，因爲我們的目標是計算Class 1的機率，所以會看到我們的式子裏面的x3的計算是1-f(x3)
我們的目標就是找到最大的w和b（w*, b* = arg max L(w, b)）,然而這件事會等同於找到一組最小的負nature log 的 L(w, b)：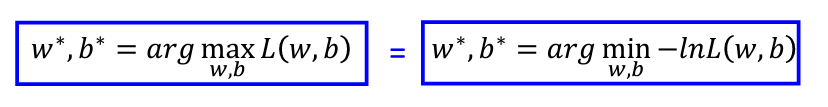

why

爲什麽要不要使用左式，而要使用右式？這是因爲本來的式子是乘法，通過取-ln，我們就可以把原本的式子轉換成加法，也就是：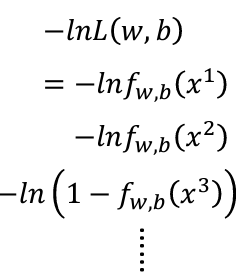

可是這樣又有一個問題，那就是這樣的式子也不太好處理，因爲沒辦法用一個summation來代表（因爲不同的class需要用到不一樣的function），所以我們可以把本來的data set的標簽處理一下，把class 1設爲1， class 2 設爲0：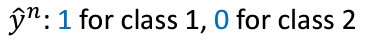

這樣我們的公式就可以轉換成下面：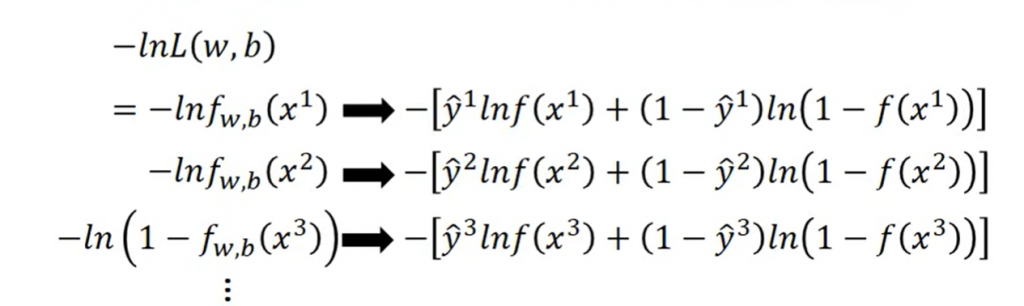

上面這段過程其實就是對數似然函數（log-likelihood function）轉換為交叉熵損失函數（Cross Entropy Loss）的過程。
總結一下，我們的推導過程中式子的變化就會是：

找到最好的Function

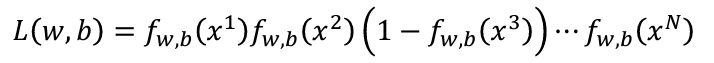
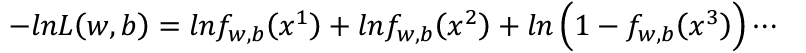
上面我們得到了衡量function好壞的式子：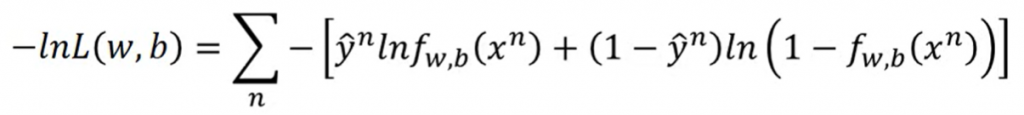

這邊如果對這個式子做了一系列的數學運算后，會得到：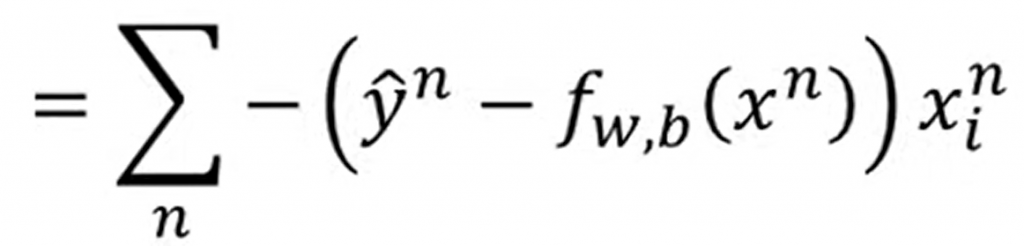

現在我們就可以使用Gradient Decent對參數進行更新：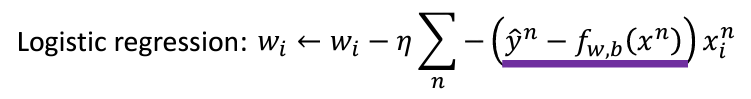

今天這章的内容參考自李宏毅教授的公開授課影片，公式、圖片都來自李宏毅教授的PPT：鏈接