在上一篇中，我們從一個Bernoulli distribution 的 Maximum Likelihood Estimation 的公式推導出了Cross-entropy損失函數的公式，以防有人沒學過或忘記，今天我想再來聊聊有關Cross-Entropy 交叉熵這個概念。

理清思路

在講解有關交叉熵以及熵是什麽之前，我想先來聊聊我們在機器學習的目標是什麽，以防止有人在錯誤的道路上越走越遠……
首先，在機器學習的領域裏，我們的目標是讓機器去找一組函數的過程，這個找出來的函數，我們稱之爲模型，而這個找出來的模型，需要和我們人類的大腦裏面的模型是最相似的一個。當然，這個是我們的終極的目標。
但是在我們實現我們的終極目標之前，我們需要有一個中間的目標，那就是找到一個方法來對比我們人腦裏的模型和機器找到的模型。但是這邊我們會遇到一個問題，那就是如果我們想要量化我們的衡量，我們需要找出一個方法有效比對兩個模型之間的差異，如果這兩個模型是同分佈，那就好辦；但是如果我們的模型是不同分佈，我們就需要一些手段來處理他們之間的差異了。

交叉熵

接下來不用猜也知道了，我們説的特殊手段就是利用了熵這個概念，把模型轉換成熵這個數值，然後再用這個數值去比較不同的模型之間的差異。

why

因爲如果是同樣的類型，比如説Gaussian distribution，就是一個期望值和一個變異數，兩個同分佈的模型間比較這兩個數值就可以了，但假如今天是Gaussian 和 Bernoulli distribution，他們之間沒有一個可以直接比較的東西，因此我們需要一個統一的單位來衡量不同模型之間的差異。

熵

維基百科的介紹：

熵被用於計算一個系統中的失序現象，也就是計算該系統混亂的程度。熵是一個描述系統狀態的函數，但是經常用熵的參考值和變化量進行分析比較，它在控制論、機率論、數論、天體物理、生命科學等領域都有重要應用，在不同的學科中也有引申出的更為具體的定義，是各領域十分重要的參量。

根據維基百科的介紹，我們可以畫一些重點，比如系統混亂的程度、描述系統狀態的函數、用熵的參考值和變化量進行分析比較，聽到這些描述感覺有些雲裏霧裏的，所以在搞懂熵這個詞之前，我們可以先來瞭解一下什麽是信息量。

比如我們看到一些教學影片，這個教學影片教的東西但凡是一個小學生都會，那麽這個影片的信息量對你而言是極小的；加入你今天在學習Machine Learning的知識，你無論如何都看不懂ELBO（Evidence Lower Bound）是什麽是什麽，於是你上網找了一個教學影片，講得十分好你一聽就懂，這隻影片對你而言的信息量就是巨大的。

所以這個信息量可以表示一些什麽呢？具體來説，就是他可以給你帶來多大的確定性。比如説籃球比賽，在8強的時候隊伍A和隊伍B的奪冠機率可能都是1/8，但是有一天有人和你說，隊伍B進入決賽了了，這時候你的確定性就從1/8來到了1/2。

通過以上的例子，可以看出若是我是隊伍B，我在8強時奪冠的概率，會等於我在4强時勝出和決賽時勝出的概率相加：

f(1/8) = f(1/4) + f(1/2)

但是滿足這一條件還不夠，因爲如果隊伍B要奪冠，必須要先進四强再進決賽，這個不是一個獨立的事件，因此要相乘：

P(隊伍B奪冠) = P(隊伍B四强勝出) * P(隊伍B決賽勝出)

所以我們可以通過這兩個條件推斷出：

f(x1 * x2) = f(x1) + f(x2)

那麽我們今天就可以給出一個定義：

f(x ) := -log_2 x

爲什麽這裏的底數是2？那是因爲我怕可以通過bit去衡量，比如説我今天有一個1/2^3，我從這樣的一個概率到確定了答案後，我得到的值是1，那麽我從1/2^3到1之間的信息量可以怎麽衡量呢？那就是3bit。

那麽熵和信息量有什麽關聯呢？其實熵就是把整個系統看成一個整體，它帶來的信息量是多少。
熵的定義：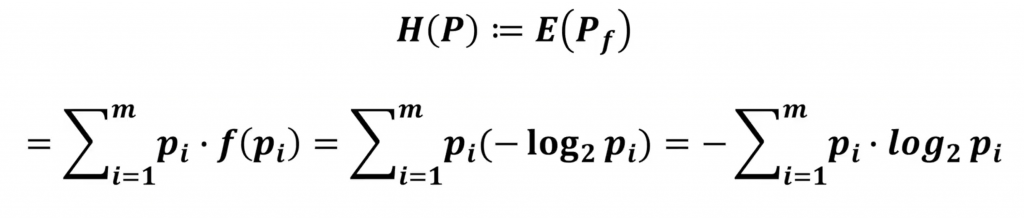

可以看到把整個系統裏面可能發生的事件，它的信息量求出來然後和該事件發生的機率相乘，最後把所有事件加起來就得到了系統熵。