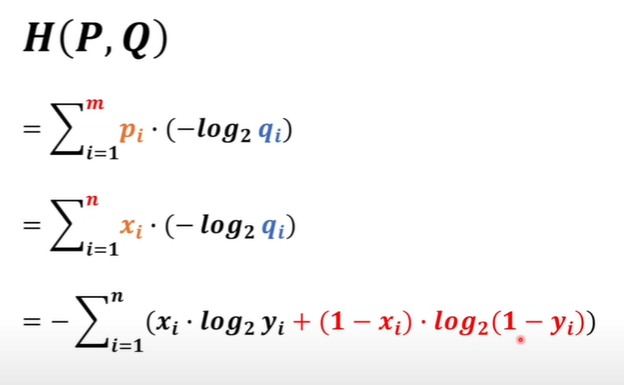昨天我們學習了關於熵的知識，知道了熵是一個用來衡量系統的混亂程度（即對信息量的不確定程度），這個熵就像是一個統一的貨幣，可以用來幫助我們衡量不同的模型，但我們還沒説到底爲什麽要用交叉熵這個方法來進行衡量，今天就讓我們來聊一聊這個話題。

模型比較

可能有的人很聰明，想到可以直接計算出兩個不同的模型的熵，然後進行比對，但是這樣過於簡單粗暴，而且試想一下，和我們機器算出來的模型比對的模型是什麽？是我們腦袋裏的那個模型，我們是沒有辦法直接對我們腦袋裏的模型求熵的。

所以，我們需要另外一個概念，叫做相對熵，也叫KL散度（Kullback-Leibler divergence，簡稱KLD）。既然叫做“相對”，那麽就代表了需要有兩個機率系統，我們可以從字面意思就理解到這是一個系統對於另外一個系統的熵。

假設我們有兩個不同的機率系統（模型），那麽計算這個KL散度的方法，就是將一個系統的信息量減去另外一個系統的信息量，然後再去求整體的期望值：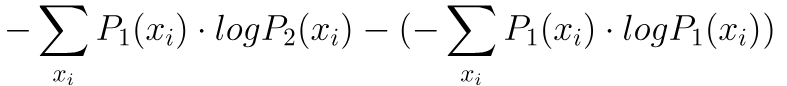

從上面式子可以看出，後半段的部分其實就是P1的熵，而前半段是什麽？那就是P1的交叉熵H(P1,P2)。
當我們的交叉熵等於0的時候，P1和P2是最接近的。我們現在就來看我們的這個式子，他的後半段P1的熵一定是大於0，前面的交叉熵也會大於0。
我們現在把上面的式子再推導一下，就會得出以下相對熵的式子：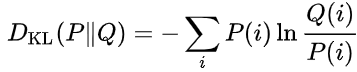

通過公式可以看到，我們是以P為基底，去考慮P和Q之間的差距。

現在問題來了，不論這個交叉熵是大於後半部分還是小於後半部分，都表示了這兩個模型越來越不象，但是我們現在希望交叉熵要不大於後半段，要不小於後半段，於是我們需要用到吉布斯不等式來證明：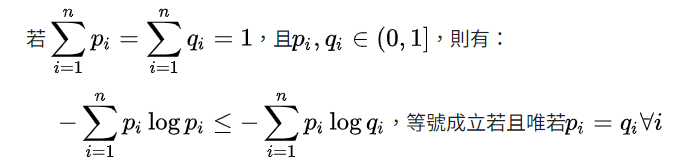

這樣，我們就能確保我們的KL散度一定是大於等於0的。當P1和P2相等的時候會等於0，不相等的時候大於0。

推導出我們的交叉熵損失函數：