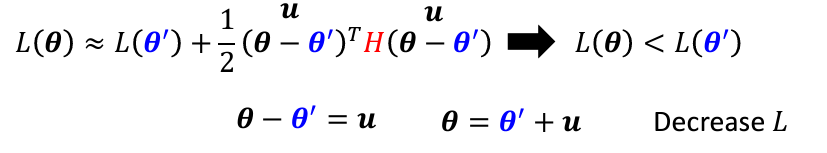在上一篇文章中，我們介紹了什麼是梯度 (Gradient) 和梯度下降 (Gradient Descent)，並舉例說明了學習率 (learning rate) 的作用。昨天我們提到了「局部最小值 (local minima)」，今天我們將進一步討論模型訓練過程中常見的問題——局部最小值與鞍點 (saddle point)。

訓練過程中的問題

在訓練模型時，隨著參數的更新，Loss 通常會逐漸下降。但在某些情況下，Loss 可能會停滯，即使我們認為模型還有改進空間，卻無法繼續下降。這時，我們需要探討可能導致訓練卡住的原因。

為什麼會卡住呢？回顧一下，梯度下降依賴於函數梯度的反方向進行更新。如果某一點的偏微分為 0，梯度下降將無法繼續前進。

臨界點 (Critical Points)

訓練過程中，當模型卡住時，我們通常認為是因為陷入了局部最小值。這是因為梯度下降的初始值是隨機的，可能會帶我們進入一個局部谷底，即局部最小值。然而，這不一定是全局最小值。

除了局部最小值，鞍點也是訓練卡住的另一個原因。鞍點的形狀像馬鞍，前後翹起，兩側較低，且在該點的偏微分也為 0。

這兩種情況都可能導致訓練停滯，因此我們將這類點統稱為「臨界點」。

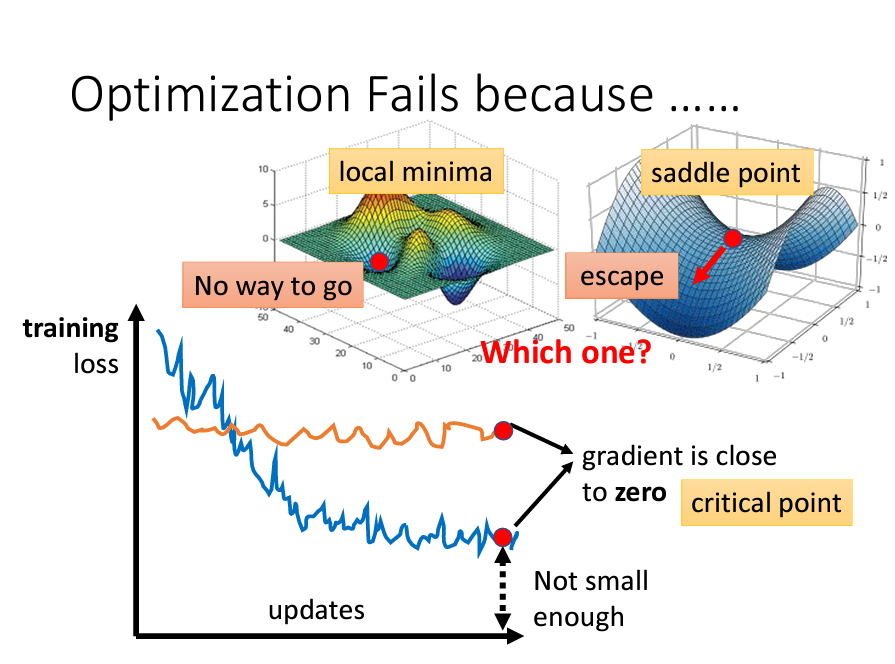
當訓練模型卡住時，我們需要判斷當前的臨界點是局部最小值還是鞍點。如果是局部最小值，代表我們已經達到該區域的最低點；而如果是鞍點，則仍有下降空間，Loss 可以進一步優化。

判斷局部最小值或鞍點

那麼，我們如何判斷當前的臨界點是哪一種呢？可以透過泰勒級數來幫助分析。其公式如下：

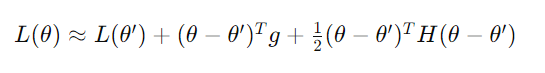
符號解釋：

1. θ：自變量（優化問題中的參數向量）。
2. θ′：展開點，通常是當前的參數值。
3. L(θ)：損失函數。
4. L(θ′)：當 θ = θ′ 時，L(θ) 和 L(θ′) 非常接近。
5. g：在 θ′ 處的梯度，即 ∇L(θ′)（一次微分）。
6. H：在 θ′ 處的 Hessian matrix，即二次導數矩陣（二次微分）。

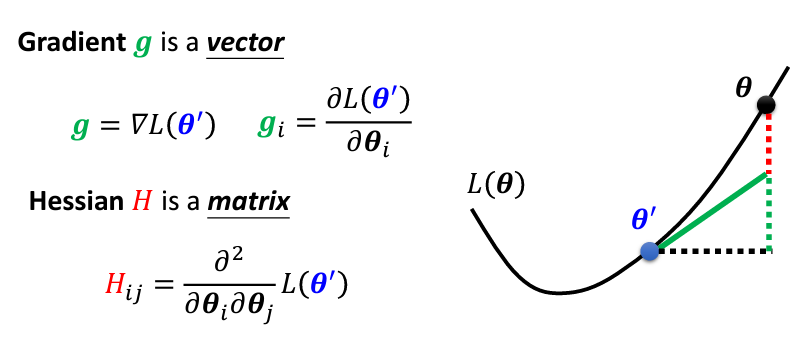
該公式表示的是在 θ = θ′ 附近，將目標函數 L(θ) 用二次多項式進行近似，從而更容易分析和優化目標函數。如果此時我們處於臨界點，公式中的梯度項（綠色框）將為 0，損失函數近似等於 L(θ′) + 紅色框部分：

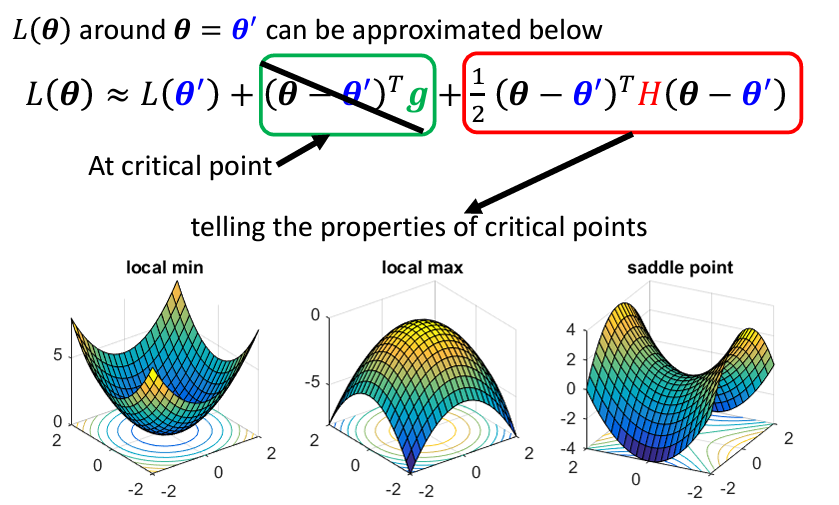
接下來，我們可以根據 Hessian matrix 來判斷 θ′ 附近的形狀。為了方便起見，我們將 θ - θ′ 替換為向量 v 表示：

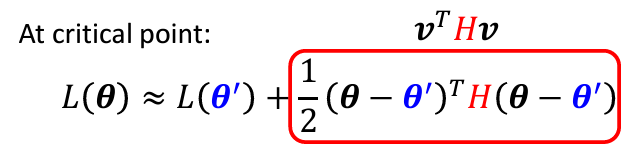
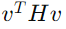這個式子用來判斷不同方向上的曲率，代表某方向 v 上的 Hessian 值的內積。根據這個值的正負，可以判斷臨界點的性質：

對於所有的𝑣：

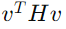• > 0 表示為Local Minima
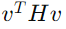• < 0 表示為Local Maxima
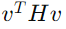• 有時 > 0， 有時 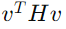< 0， 表示為當前的點所在的地方正處於Saddle Point

不過，這樣逐個方向進行計算會非常低效，因此我們可以通過計算 Hessian matrix 的eigen values來判斷：

• 𝐻 is positive definite = All eigen values are positive - Local Minima
• 𝐻 is negative definite = All eigen values are negative - Local Maxima
• Some eigen values are positive, and some are negative - Saddle Point

鞍點的突破方法

Hessian matrix 不僅能幫助我們判斷當前地形，還能指出參數更新的方向。在訓練過程中，當走到臨界點時，梯度項 g 為 0，因此我們無法依賴梯度更新參數，此時需要依賴 Hessian matrix。如果確定處於鞍點，我們可以進行以下操作：

假設𝒖是 H 的特徵向量，𝜆是其對應的特徵值。我們將 v 替換為𝒖，得到：

這表示我們可以將參數向量沿著𝒖方向進行移動，從而降低 Loss：