在上一篇文章中，我們討論了局部最小值 (local minima) 和鞍點 (saddle point)，解釋了為什麼在訓練模型時會卡住，以及如何判斷當前位置是局部最小值還是鞍點，並介紹了如何從鞍點中脫困。今天，我們將繼續探討模型訓練中的「批次」(batch) 概念，並介紹一種常見的優化演算法：動量法 (momentum)。

批次處理

在進行梯度下降 (gradient descent) 的過程中，我們通常會將整個數據集 (data set) 分割成多個批次 (batch)。假設我們的數據集共有 N 筆資料，會隨機將其切割成多個批次，每個批次包含 B 筆資料。與其一次性使用所有數據來計算損失函數 (loss)，我們改為在每個批次中計算該批次的損失，並基於該批次的結果更新模型參數。并且我們在把資料分成一個一個batch的時候，我們會做一個shuffle的動作，最常見的做法就是在每一個epoch開始前我們會隨機的去分batch，所以我們每一個epoch的batch都會不一樣。

具體過程是：從第一個批次開始，我們計算該批次的損失函數 (L_1)，更新參數後，再使用下一個批次的資料來計算損失函數 (L_2)，並再次更新參數。如此反覆進行，直到所有批次都被遍歷一次，這個過程稱為一個「時代」(epoch)。

因此，每一次參數更新並不是基於整個數據集的損失 (L)，而是基於每個批次的損失 (L_1, L_2, ..., L_B)。每次更新參數的過程被稱為一次「更新」(update)。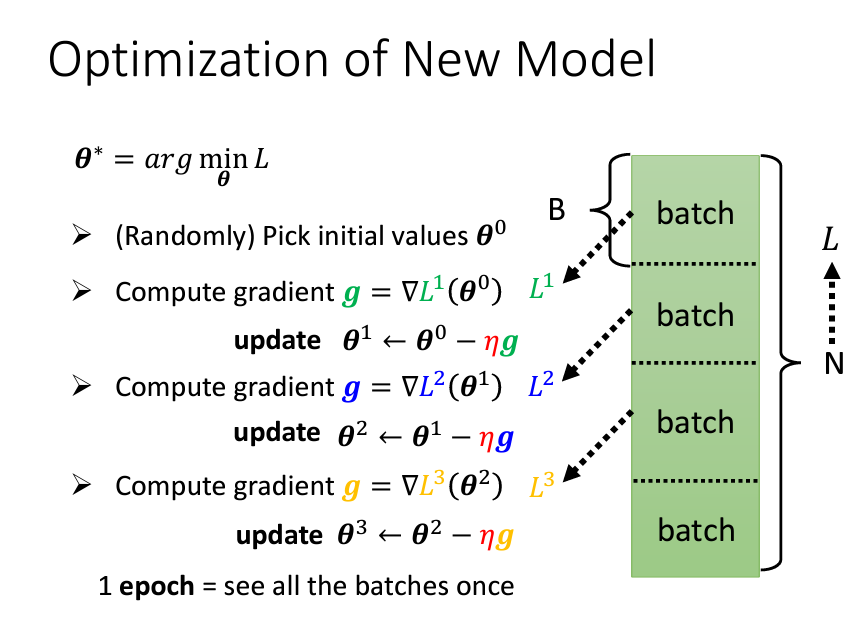

假設：

• 有10000筆資料（N = 10000）
• Batch Size 大小是 10 （B = 10）
  那麽1 epoch就會有1000次update

• 有1000筆資料（N = 1000）
• Batch Size 大小是 100 （B = 100）
  那麽1 epoch就會有10次update

爲什麽分批次

至於爲什麽要把資料分割成多個batch呢？我們可以看下圖：

這張圖的左邊就是儅我們的batch size = N的時候，也就是沒有分batch；右邊是當我們的batch size = 1的時候，那麽我們每看一筆資料就更新一次參數。可以看到的是，當我們分多個batch的時候，我們的參數更新會比較快，但卻是noisy的，也就是會很大幅度的震蕩，而一次過看全部資料的雖然更新比較慢，但卻是走得很穩。

但是事實上一次過看N筆資料真的比較慢嗎？那可不一定。當我們考慮用GPU去平行運算的時候，我們會發現其實分多個batch，只要你不要分的太多而超出GPU的能力範圍，基本上分batch和部分batch差不了太多，反而如果我們看每次更新參數和每個epoch所花的時間，會發現他們是倒過來的：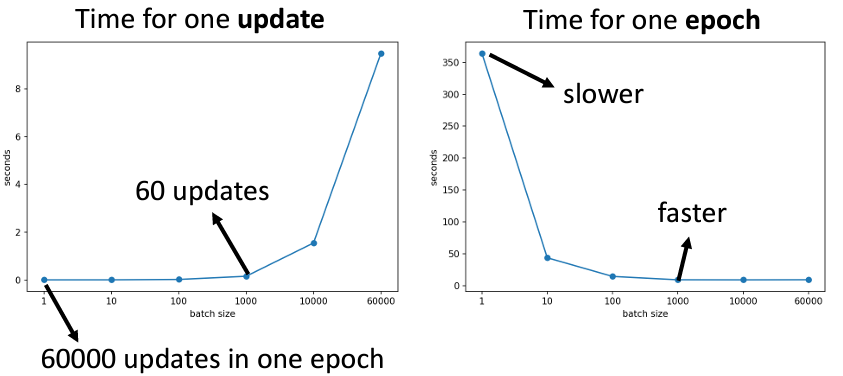

Batch Size 大和小的區別

但是這樣一來，我們就會發現難道大的batch就沒有劣勢了嗎？他本來跑的慢的缺點，但是現在通過平行運算加速了，大的batch就只剩下優勢了嗎？
但如果我們通過別人的研究數據就會發現，在小的batch size上，我們的performance，我們在比較noisy的方法反而是比較好的：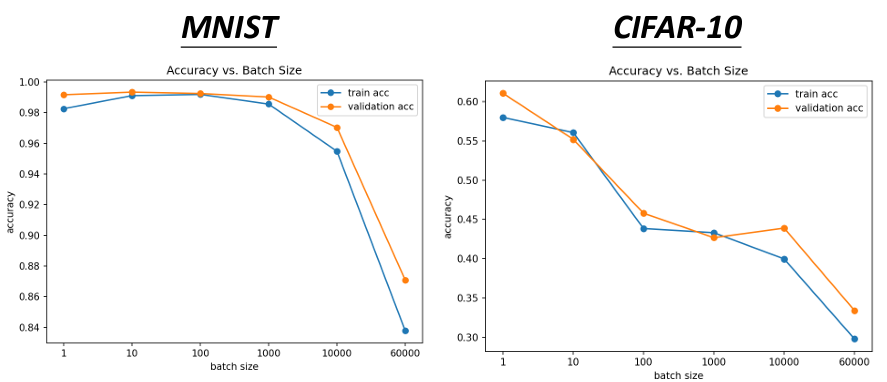

有一個可能的解釋：
就是當我們每次跑gradient decent，我們可能遇到一個critical point，我們的gradient decent就卡住了這樣，但是儅我們的batch size小的時候，update的次數比較多，所以你在上一次卡住的地方，我下一個batch可能不會卡住：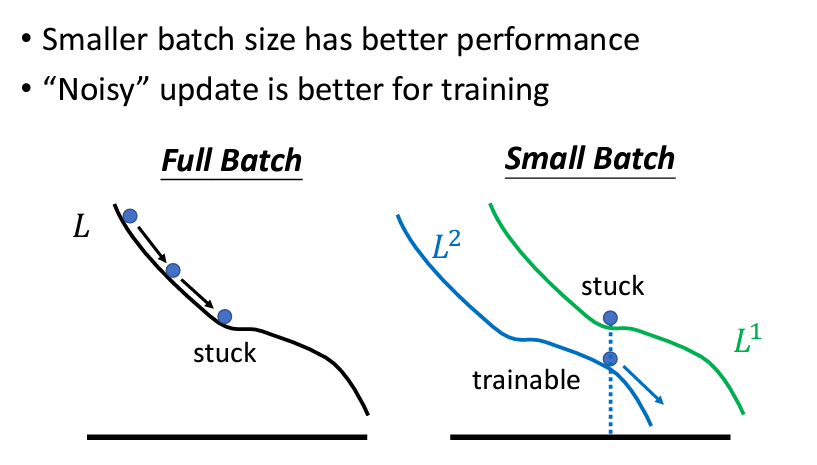

而且不僅如此，小的batch可能還會再testing set的表現上取得更好的成績，這是因爲local minima也有分好的minima和壞的minima，通常我們會説在一個比較平坦的minima是比較好的minima，那是因爲我們的training set 和testing set如果是有一些差距的話，可能是distribution不一樣，可能是sample到的資料不一樣造成的，無論如何，當我們在一個比較平坦的峽谷，我們在testing set依然不會相差太大，但是在一個v字形的峽谷的話就不是這樣了，因爲兩邊較陡峭的關係，所以在training set上表現好可是testing set上表現會差很大：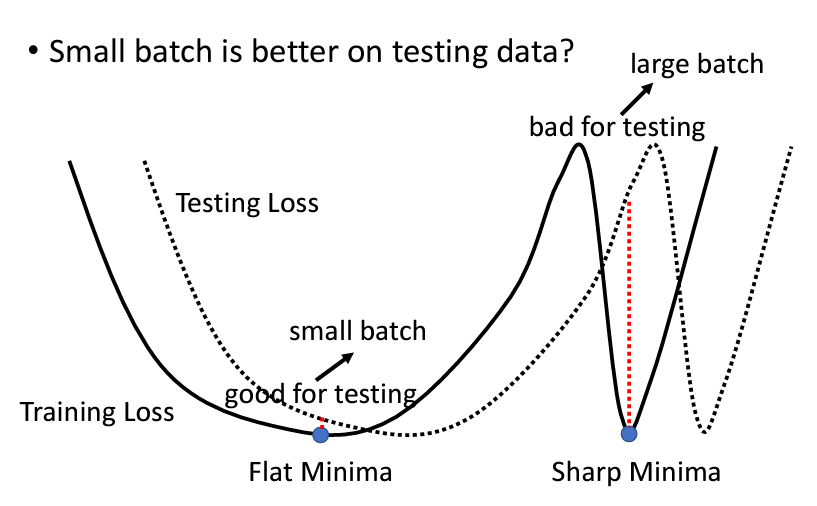

Momentum

Momentum跟gradient decent一樣是一種優化算法，但是Momentum是一種有可能對抗Saddle Point或Local Minima的技術。Momentum是參考了現實的物理世界裏面的動量：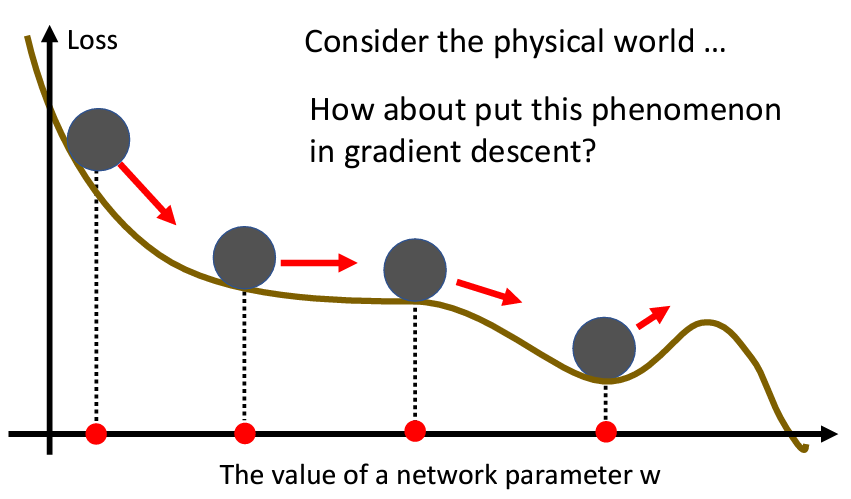

假設你今天有一顆球從山坡上滾下來，遇到了saddle point或local minima，會因爲速度很快的關係，是有可能越過saddle point或local minima的。

具體要怎麽做呢？那就是在原本的gradient decent上加上momentum，原本的gradient decent是根據梯度來決定方向，learning rate來決定移動的距離。加上momentum了以後，就會變成不止往gradient的反方向去移動，而是gradient的反方向+前一步移動的方向：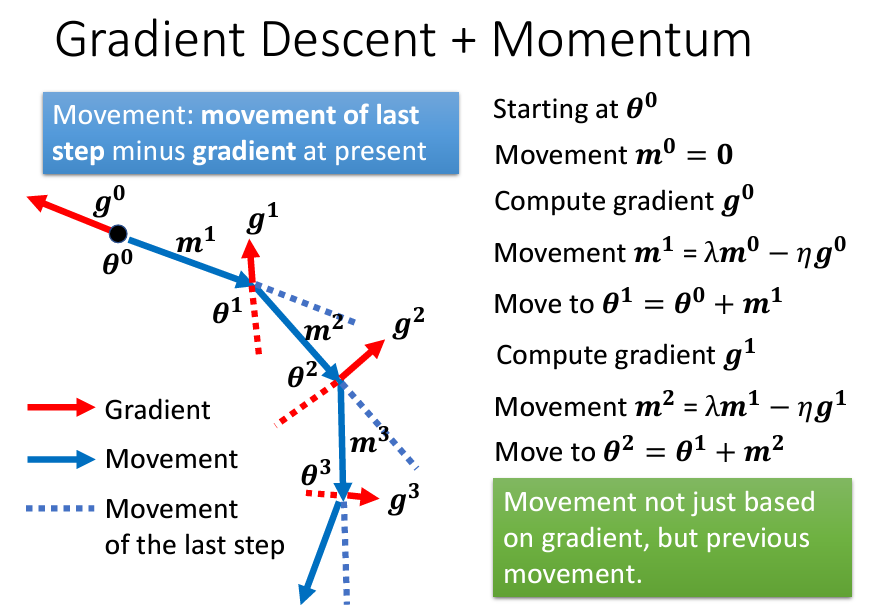

那個m就是我們每一次的移動，可以寫成之前所有算出來的gradient的weight的加總：

以上的内容來自於臺大教授李宏毅：鏈接，我只是把他的影片寫成了筆記。