引言

昨天我們完成了茱莉亞合集的渲染，能夠根據滑鼠的位置改變常數 C，從而渲染不同的圖形，今天我們將探討另一個經典分形——曼德柏羅集，這個集合將初始值設為 0，用不同的座標代表不同的複數常數 C，並測試它是否會發散或收斂。

同時，我們還會探討如何通過片段著色器添加不同的顏色渲染方式，並簡單實現反鋸齒（Anti-Aliasing）。

相關公式

在這三個分形圖形中，我們今天會完成後面兩個：

1. Julia Set：
   

2. Mandelbrot Set：
   

3. Burning Ship Fractal：
   

片段著色器

首先我們先準備座標軸，我們希望寬度會是畫布中的 2 個像素點。因為是放大過的座標，我們需要除以 zoom 來取得相對的座標，接著我們可以在末尾用 GLSL 內建的 step 和 mix 方法來進行混色：

1. color：先將計算出來的顏色儲存起來。
2. step(a, b)：該函式會根據條件 b > a 的時候輸出 1，反之是 0。因此可以用這個特性來繪製座標軸，效能會比 if else 來的好。
3. mix(c1, c2, value)：該函式會根據輸入值 value 來混合兩個顏色。

曼德柏羅集

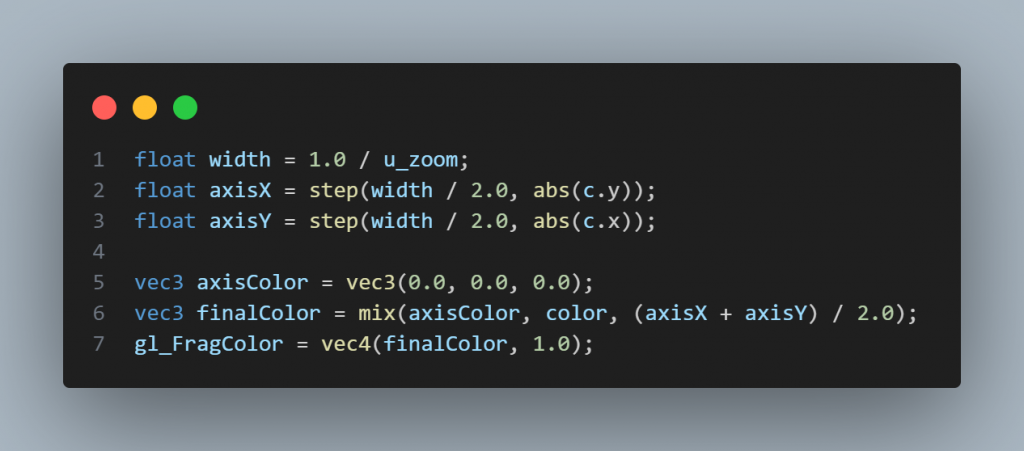
在曼德布羅集的渲染中，我們需要將初始點設為 0，並根據座標判斷不同的 C 是否發散。第三種圖形其實是曼德柏羅集的變體，在每次迭代的時候會套用絕對值，因此我們可以用一個條件 transform 來達到兩個圖形的過渡：

顏色渲染

為了增加色彩層次，我們可以使用三角函數來變換顏色。透過為 sin 和 cos 設定不同的週期，來顯示更豐富的細節：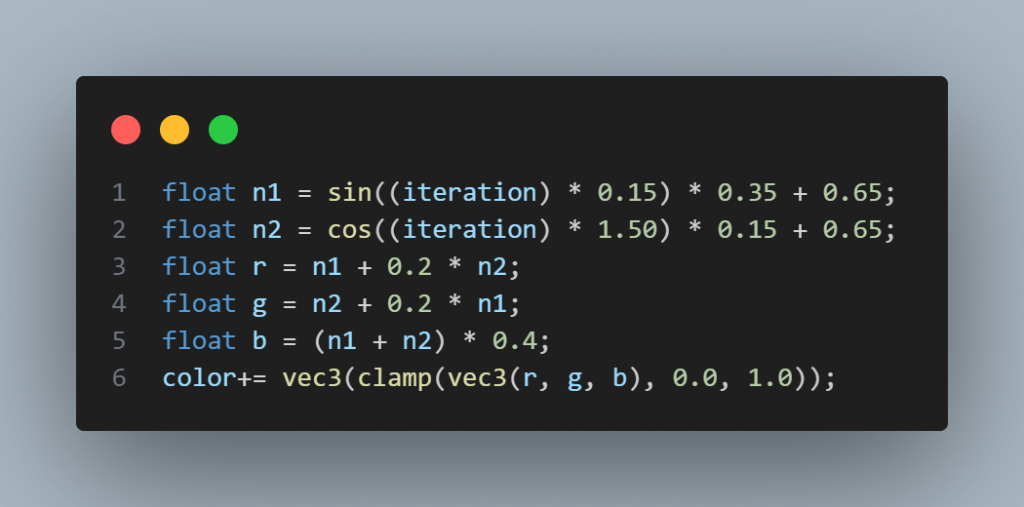

透過這個方式可以看到圖形的細節更加明顯，並且能明顯看到迭代的痕跡。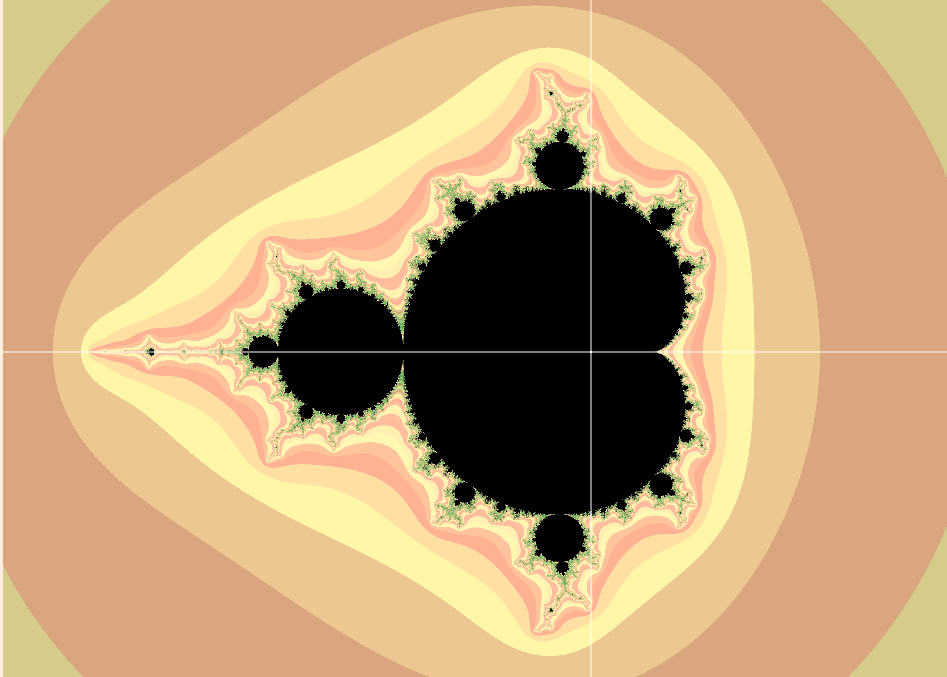

尤其是放大之後更加明顯：

AA 反鋸齒

接下來讓我們實現 AA 反鋸齒，對於隨機數的取用我們需要一種算法，這是其中一種偽隨機數的生成方式，足夠生成具有隨機性質的數據如噪聲、抖動效果：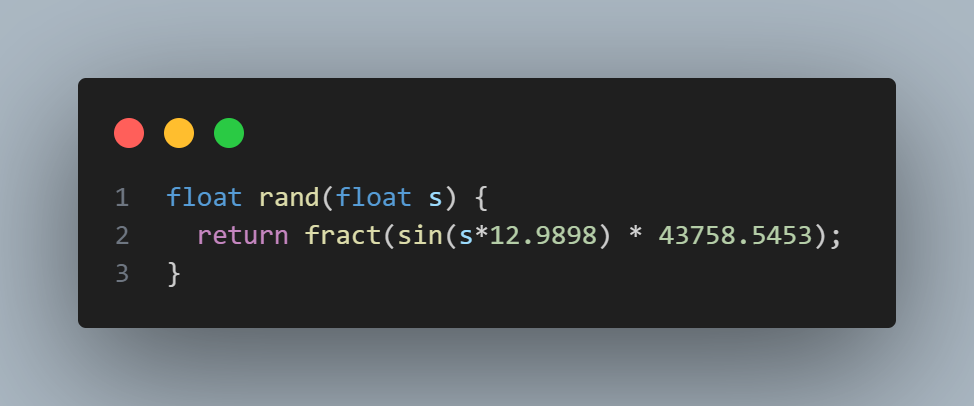

• fract()：最終用這個函數返回數值的小數部分，得到 0 ~ 1 之間的值。

接著，我們用迴圈進行多次取樣，最後取得顏色的平均值，達到平滑過渡的效果：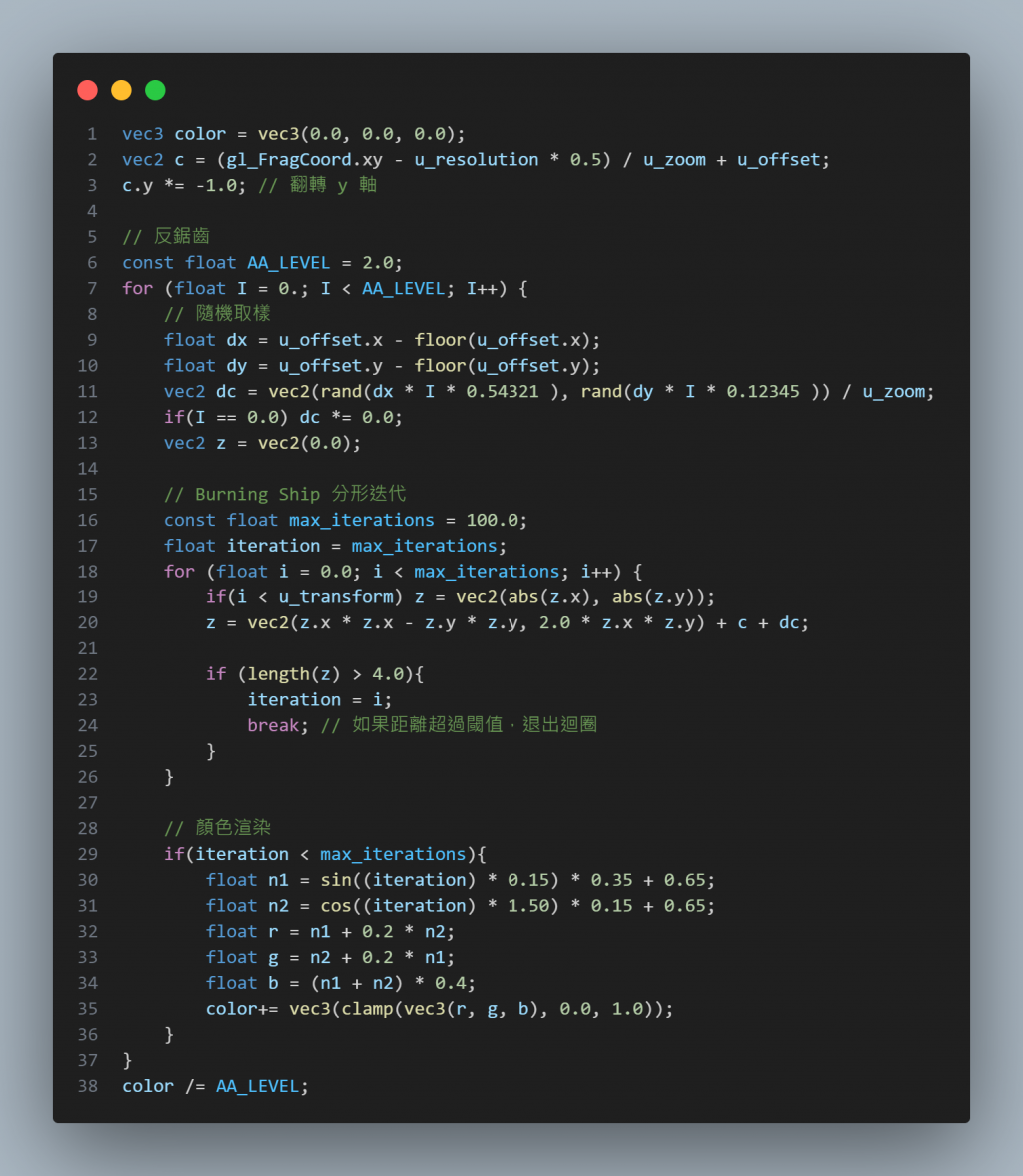

• dx, dy：用每個像素的小數部分來隨機偏移。
• rand()：將小數乘上索引值和特殊常數後，計算對應的隨機小數。

為了隨機取樣，每個像素點重複做了多次的迭代，因此要謹慎設計反鋸齒的迴圈次數已平衡效能。另外一點是，WebGL 中，條件式必須用常數判斷，所以無法在 Javascript 動態輸入反鋸齒的迴圈次數，這也是一個潛在問題。

結論

透過今天的學習，我們進一步了解了如何渲染複雜的分形圖形，如曼德布羅集和其變體。同時，我們學會了使用片段著色器來處理顏色漸層和三角函數，增加圖形的細節與美感。此外，我們還探索了如何實現簡單的 AA 反鋸齒，提升畫面的平滑度。

參考我的 github：

• gh-page
• fragmentBurningShip.glsl