引言

透過前兩天的範例，我們已經理解了頂點著色器和片段著色器的分工模式，頂點著色器負責處理頂點的空間定位，而片段著色器則專注於每個像素的渲染工作。接下來，我們將專注於片段著色器，來渲染一個著名且充滿神秘美感的數學圖形——茱莉亞集合。這很適合我們學習如何為每個像素點著色。

茱莉亞集合

茱莉亞集合是一個來自複數平面的分形，它展現了複雜而對稱的圖形結構。透過反覆計算複數的二次方程式，我們可以視覺化這些複雜的數學結構。作為著名的「分形」，它能在無限放大下顯現出越來越多的細節。這使得它成為數學和計算圖形學領域的經典範例。

相關公式

在這三個分形圖形中，我們今天先完成第一個：

1. Julia Set：
   

2. Mandelbrot Set：
   

3. Burning Ship Fractal：
   

片段著色器

對於茱莉亞集合，我們需要完成三個步驟：

1. 實現複數乘法
2. 計算複數座標
3. 渲染顏色

1.實現複數乘法

這裡，我們定義了一個名為 complexMul 的函數，用於進行複數的乘法運算。其中 [x, y] 表示實部和虛部

2.計算複數座標

為了渲染座標平面，我們需要有一個方法來描述原點的位置，和兩個軸向的尺度：

• gl_FragCoord.xy 是當前片段的螢幕座標，代表像素位置。
• u_resolution * 0.5 是畫布的中心點，將像素座標平移，使中心對齊。
• u_zoom 是用於縮放的變數，將像素坐標縮放到適合的範圍。
• u_offset 是用於平移的變數，進一步調整座標。

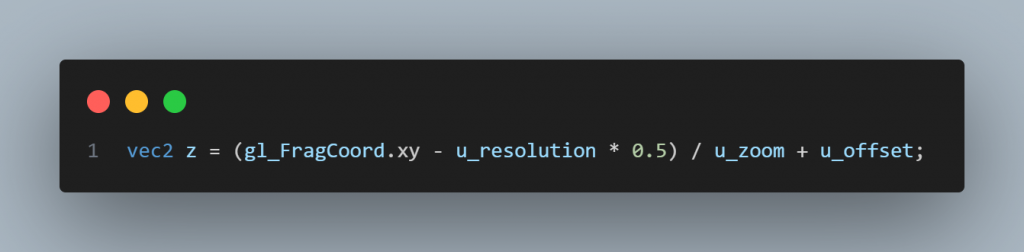
我們首先將當前像素的座標轉換為相對於畫布中心的複數座標，接著依序進行縮放和偏移。

3. 渲染顏色

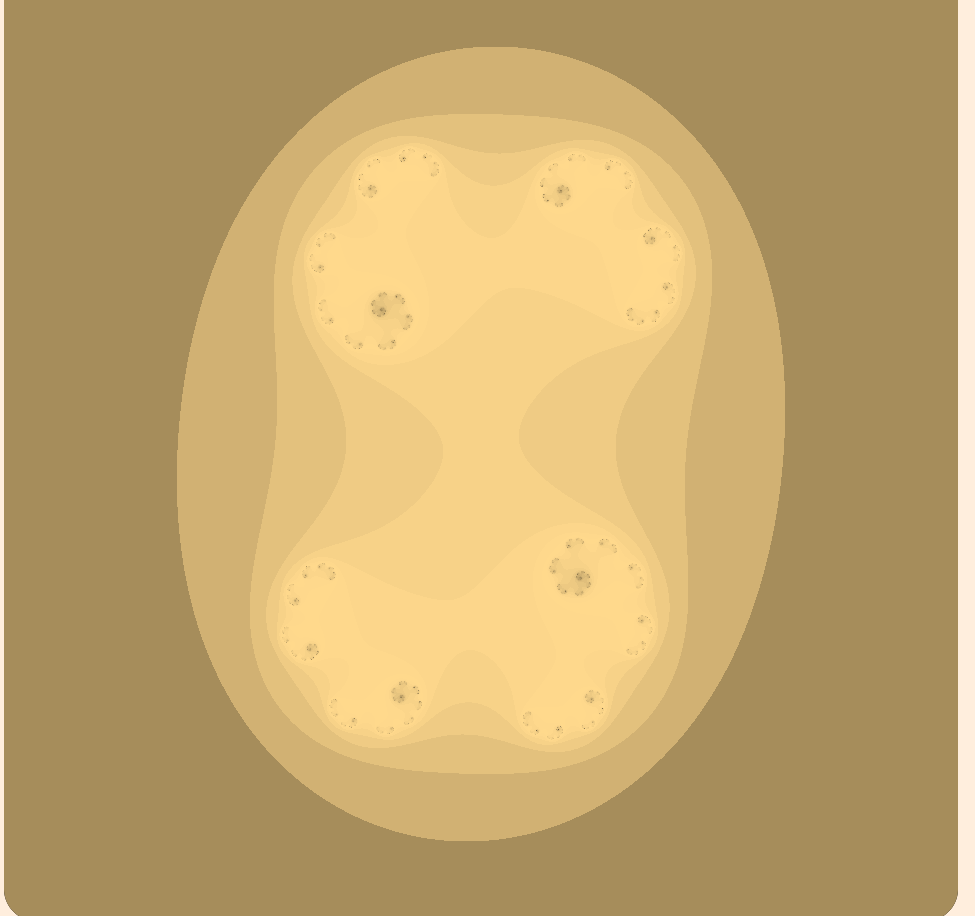
接著是分形渲染的主要邏輯之處，用一句話說：「如果該點離原點越來越遠，就視為發散，結束遞迴」，在這裡我們設置迭代的上限為１００次，假如能夠完全迭代，就不進行著色（黑色）：

• dot(z1, z2)：計算兩個向量的點積，用兩個相同的點計算，相當於 x^2 + y^2。

在顏色方面，使其隨著迭代次數增加產生變化，除了單純的漸層外（方法一），我們也可以加入三角函數，讓顏色有更多層次和波動（方法二）。

畫面的放大縮小和偏移

接下來還有些時間，來聊聊怎麼實現這些參數的計算，對於事件的處理如下所示，由於相對複雜，因此事件到時候會另開一篇講解：

return (
    <section ref={section} className="section" id={sectinoID}
        onMouseMove={handleMouseMove} onWheel={handleWheel}
        onMouseUp={handleMouseUp} onMouseDown={handleMouseDown}
        onTouchStart={handleTouchStart}
        onTouchMove={handleTouchMove} 
        onTouchEnd={handleTouchEnd}>
    </section>
);

首先我們要了解一件事情，先後順序是很重要的，如果先放大在偏移，就意味著修改縮放值會影響到偏移。因此我們要區分兩種情況。

1.修改偏移

我們希望滑鼠在移動的時候，會有些許延遲效果，這邊也是用系列文 A2 的動畫物件所實現的。雖然我們已經有滑鼠的延遲座標可以用，但我們希望有獨立的動畫效果，所以我們可以用 target 來取得滑鼠的真正座標來使用。

const addOffsetX = (myMouse.targetX - preMouse.current.x) / zoom * 50;
const addOffsetY = (myMouse.targetY - preMouse.current.y) / zoom * 50;
preMouse.current = {x: myMouse.targetX, y: myMouse.targetY};
setOffsetX(offsetX - addOffsetX);
setOffsetY(offsetY + addOffsetY);

• 1 / zoom * 50：局部放大相當於切割像素，50 則是給 input 格式化用的常數。
• preMouse：用 ref 來容納數據，儲存上次滑鼠的座標
• Y 軸是相反的（昨天的頂點著色器，我們用[1, -1]來映射[x, y]）

總而言之，偏移比較單純，就是根據當前的畫面比例，來計算滑鼠每移動一個像素，著色器需要移動多少像素座標。

2.修改縮放後影響偏移

然而，縮放的時候，也會讓偏移改變，這是因為我們在計算複數座標時，會隨著縮放等比例放大。因此，我們可以先把座標回歸原點來解決這個問題。

同時，我們還希望放大的中心點位於滑鼠的位置，因此我們需要完成以下步驟：

1. 計算相對於原點的偏移量
2. 加上局部放大後的偏移
3. 減回去相對偏移回歸原點

const addOffsetX = (canvas.current.width / 2 - myMouse.targetX) / zoom * 50;
const addOffsetY = -(canvas.current.height / 2 - myMouse.targetY) / zoom * 50;
setZoom(zoom * zommIn);
setOffsetX(offsetX + addOffsetX / zommIn - addOffsetX);
setOffsetY(offsetY + addOffsetY / zommIn - addOffsetY);

如此一來，就順利完成縮放和偏移的設定囉！這樣的設定不僅能夠讓使用者更直觀地操作畫面，還能不斷地放大畫面，使我們的茱莉亞集合呈現出更加豐富的細節和美感。

結論

透過本篇文章，我們學會了如何利用片段著色器來渲染茱莉亞集合，這個過程涉及複數運算和像素著色的技術。從實現複數乘法，到計算複數座標，再到最終的顏色渲染。此外，我們還討論了如何通過滑鼠事件來實現畫面的縮放和平移，增強了使用者互動的體驗。

參考我的 github：

• gh-page
• fractalWebGL.js
• React參數狀態管理