在去年出版的書籍中提到,成本的異常檢測最簡單的是透過觀察最大值與最小值來探討。然而,真正的異常資料,其實可以用更科學的方法進行統計比較。本章節希望針對過往輔導時經常遇到的問題,提出一套更具體的解決方式,離人工智慧學校畢業已五年,期間涉略相對較淺,模型原理尚未深入探討,等有更多案例研究再來說明~
期望解決的問題
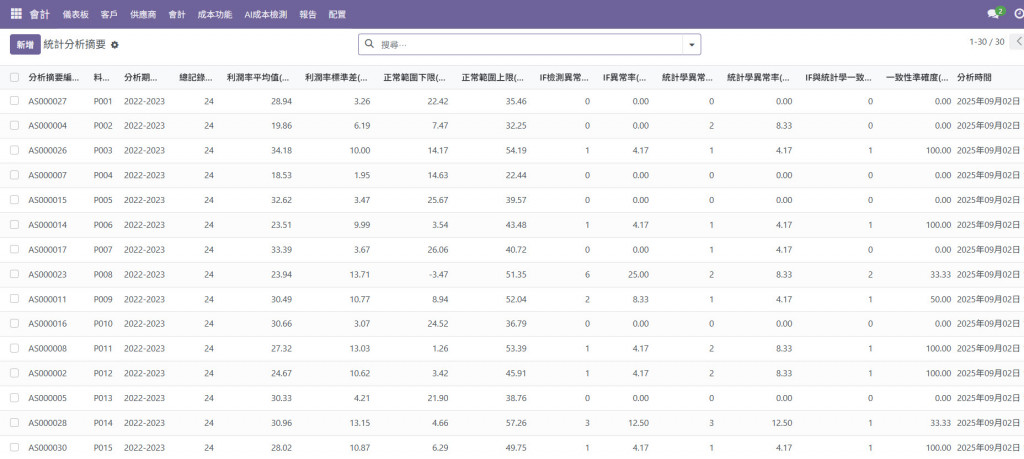
首先,我們需要建立最基礎的統計資料。只有在具備標準差等統計基準後,才能進一步判斷 AI 所偵測到的異常是否真為異常。因此,本章節將聚焦於 統計方法與 AI 模型之間的一致性比較。
當然,AI 的理論基礎與可選模型非常多元,但在本章節中,我更希望先完成 架構的實作,也就是打造一個可反覆測試 AI 的操作介面。至於模型的深入選擇與評估,則需要更多知識與測試過程,暫不在此展開。
最終目標
期望的成果是能延續 Day27 的銷貨成本毛利表,並在此基礎上加入 AI 與統計功能,讓分析更完整、更科學。
本系統在 銷售毛利分析表 中整合了統計異常檢測功能,透過 Z 分數(Z-Score) 方法來識別產品利潤率的異常情況,幫助管理者快速發現需要關注的異常交易。
1. 常態分佈假設
2. 異常檢測的實務意義
3. Z 分數公式
Z = |(當前利潤率 - 歷史平均利潤率) / 歷史標準差|
本系統整合了基於機器學習的 Isolation Forest (IF) 異常檢測演算法,透過多維度特徵分析來識別銷售毛利中的異常模式。IF 是一種 無監督學習方法,特別適合處理高維度資料的異常檢測。
多維度特徵向量(共 8 個特徵)
資料預處理
污染度 (Contamination)
異常判斷機制
predictions[0] == 1 → 正常predictions[0] == -1 → 異常min(1.0, max(0.0, score))
1. 基本原理比較
| 項目 | 統計分析(Z 分數) | IF(Isolation Forest) |
|---|---|---|
| 理論基礎 | 傳統統計學 - 常態分佈假設 | 機器學習 - 無監督學習 |
| 核心概念 | 標準化分數,衡量偏離平均值的程度 | 孤立性原理,異常點更容易被隔離 |
| 數學基礎 | 標準差、平均值計算 | 隨機決策樹、路徑長度分析 |
| 假設條件 | 資料遵循常態分佈 | 無特定分佈假設 |
2. 檢測維度比較
| 項目 | 統計分析(Z 分數) | IF(Isolation Forest) |
|---|---|---|
| 分析維度 | 單一維度(利潤率) | 多維度(8 個特徵) |
| 特徵數量 | 1 個:當前利潤率 | 8 個:利潤率、移動平均、標準差、趨勢、數量、價格等 |
| 時間考量 | 歷史平均值和標準差 | 短期、中期趨勢 + 絕對數值 |
| 複雜度 | 簡單線性關係 | 複雜非線性關係 |
**3. 異常判斷標準比較 **
| 項目 | 統計分析(Z 分數) | IF(Isolation Forest) |
|---|---|---|
| 判斷方式 | 閾值比較:Z > 2.0 | 二元分類:-1(異常)/ 1(正常) |
| 分數範圍 | 0 到 ∞ | 0.0 到 1.0 |
| 閾值設定 | 固定閾值(2.0) | 模型自動學習閾值 |
| 可解釋性 | 高(明確的統計意義) | 中等(需理解機器學習概念) |
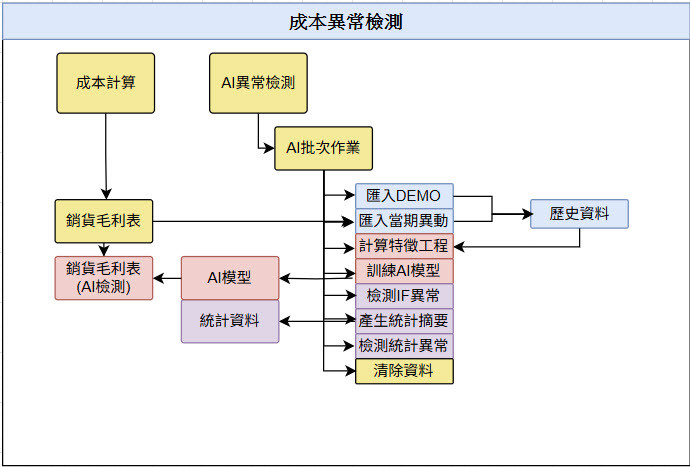
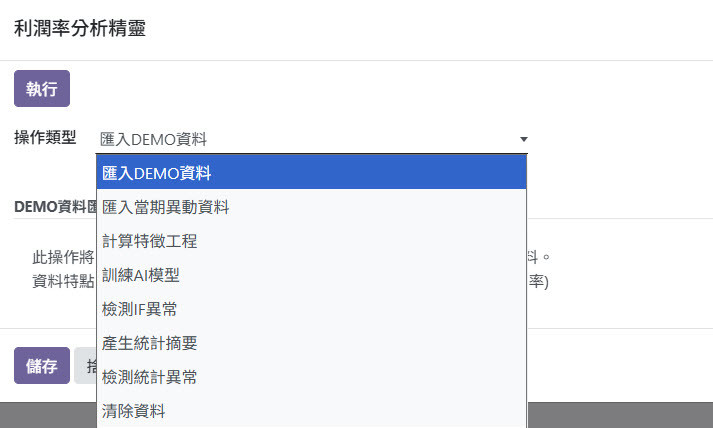
前面介紹了兩種異常檢測的架構方法,接下來就是規劃實際系統的流程。由於目前沒有真實資料,我先請 AI 簡化產生 24 期、30 個料號,共 720 筆 DEMO 資料,並設計一隻作業程式,透過下拉選單可多次產生資料。流程如下:
如果要測試不同污染度對異常檢測結果的影響,可以在 訓練 AI 模型 時重新操作。期望的效果是:AI 模型在每個月產出報表後,都能重新訓練一次,讓下一期產生銷貨毛利分析表時可直接使用更新後的模型。
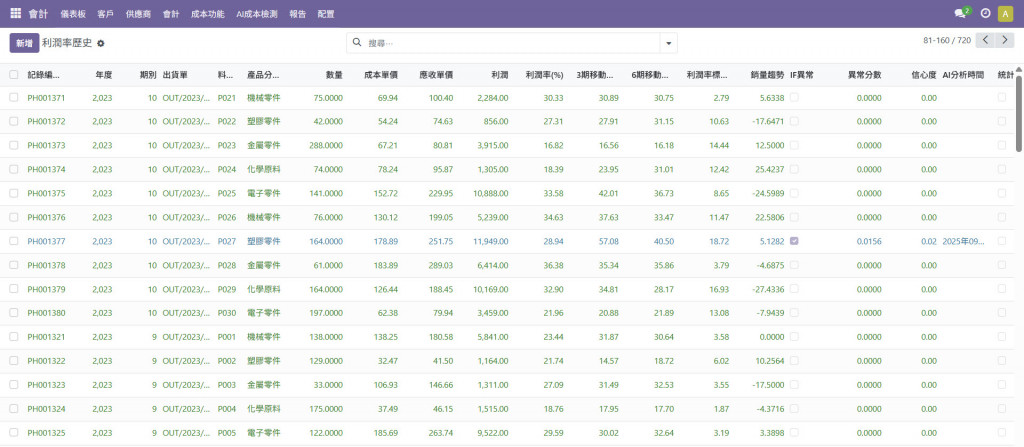
此外,最終呈現結果需要接續 Day27 的銷貨毛利分析表。由於料號略有不同,我將名稱改為 P001與P004 進行實作報表結果,讓系統在撈取報表資料後,能直接放入模型判斷,並輸出統計與 AI 的異常檢測結果,可以發現P001是統計與IF都正常,P004在統計異常,IF正常,那在統計上就是Z分數偏離太多,因此顯示異常。
實際操作畫面如下:

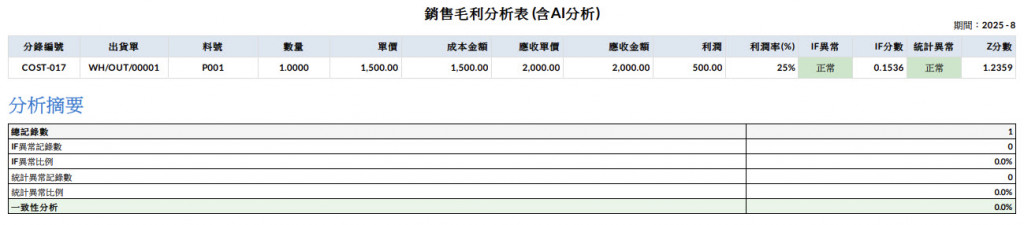
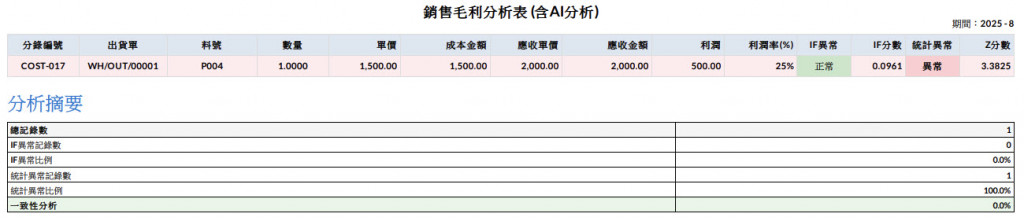
在異常檢測的實務中,過往比較常見的是人工製作一版合理的標準資料作為判斷依據,再逐一的去比較資料,但這樣的方式往往過於耗時耗力,無法大量的進行檢查,透過系統協助可以達到:
其一當然是樣本數不夠多,其二需要注意的是,這類方法同樣存在限制。當資料本身幾乎全是異常時,系統將難以分辨差異,形成所謂 「垃圾進,垃圾出」 的情況。
因此,更進階的做法可能是:
若要在實務上更廣泛應用,未來可以:
