昨天我們建立了第一個 Baseline Model,今天我們要更進一步透過 視覺化模型表現 ,來了解我們的模型是怎麼做出判斷的,並思考如何改善。
ROC 曲線 (Receiver Operating Characteristic Curve) 是評估分類模型的重要工具,能幫助我們了解模型在不同閾值(threshold)下的表現。
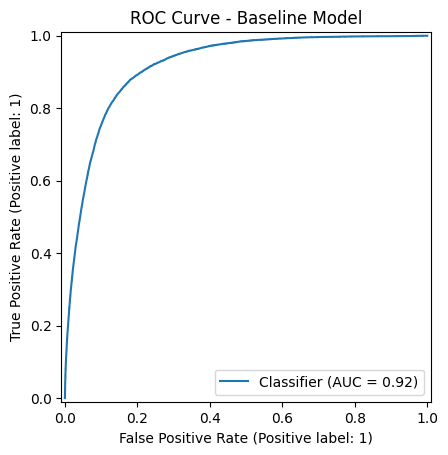
這樣講完還是很讓人一頭霧水,我們先拆開來看兩個軸:
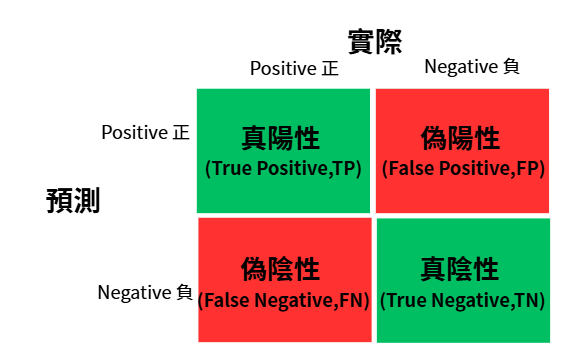
X 軸:False Positive Rate (FPR)
這個就是『被誤判的比例』。想像一下,如果模型把一個明明不該中獎的人說成中獎,那就是 False Positive。X 軸越往右,就是誤判越多。
Y 軸:True Positive Rate (TPR)
這是『抓對的比例』,也就是有多少真正該中獎的人被我們抓到了。Y 軸越往上,就代表模型越會抓人。
所以整條 ROC 曲線就是:一邊把閾值(threshold)從 0 拉到 1,一邊記錄「誤判比例」跟「抓對比例」,然後畫出來。ROC 曲線下面積把 threshold 從 0 ⟶ 1 慢慢掃過去,會得到很多組 (FPR, TPR);這些點連成的曲線下方面積,就是 AUC。面積越大,代表「在各種門檻下都能維持高 TPR、低 FPR」。
理想狀態下,這條線越往左上角靠近越好,因為那代表誤判少、抓到越多正確的。(因為機率本身定義就是介於 0 和 1 之間的數值,不會有負機率或超過 1 的機率,所以 threshold 合理的範圍就是 [0, 1]。)
import os
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import RocCurveDisplay, roc_auc_score
PROB_PATH = "/content/y_val_pred_prob.npy" #上傳y_val_pred_prob檔案存放路徑
# 畫 ROC
RocCurveDisplay.from_predictions(y_val, y_pred_prob)
plt.title("ROC Curve - Baseline Model")
plt.show()
# 算 AUC
auc = roc_auc_score(y_val, y_pred_prob)
print(f"AUC: {auc:.3f}")

在計算 AUC(曲線下面積)之前,我們要先理解 predict_proba 的輸出。對於二元分類問題,model.predict_proba(X_val) 會回傳一個形狀為 (樣本數, 2) 的二維陣列,每一列都有兩個數字,分別代表該樣本屬於類別 0 和類別 1 的機率,例如:
[[p(class=0), p(class=1)],
[p(class=0), p(class=1)],
...]
而我們畫 ROC 曲線和計算 AUC 時,會注意「正類的機率」(通常是 class=1),在這個比賽中就是會定期存款的顧客,因此要透過 [:, 1] 取出第 1 欄,把二維陣列轉換成一維向量,才能和 y_val 對應。這一步非常重要,如果忘記加 [:, 1],會導致 roc_auc_score 和 RocCurveDisplay.from_predictions 長度不匹配而報錯。
| 名稱 | 位置 | 有沒有 y 標籤? | 使用時機 |
|---|---|---|---|
| X_train, y_train | 訓練集 | 有 | 用來訓練模型 |
| X_val, y_val | 驗證集 | 有 | 用來自己檢查模型表現 |
| X_test | 測試集(Kaggle提供) | 沒有 | 用來預測結果,上傳 Kaggle 評分 |
我們在上面的程式碼寫到計算AUC,我們也需要了解AUC是甚麼才行!
前面 ROC 曲線就是:一邊把閾值(threshold)從 0 拉到 1,一邊記錄『誤判比例』跟『抓對比例』,然後畫出來,而實際上我們不用自己在那邊一直調 threshold,AUC 就可以直接幫你把所有門檻都試過之後,給模型的一張總成績單。隨機抓一個正樣本跟一個負樣本,模型把正樣本的分數(機率)排在更前面的機率。
# 算 AUC
auc = roc_auc_score(y_val, y_pred_prob)
print(f"AUC: {auc:.3f}")
把 AUC 說成「排序能力」還是很抽象,我們來舉一個例子:想像有 5 個人要判斷會不會定存(1=會,0=不會)。模型給每個人一個「越高分越會定存」的分數(機率)
| 人 | 真相 y | 模型分數 s |
|---|---|---|
| A | 1 | 0.90 |
| B | 1 | 0.60 |
| C | 0 | 0.70 |
| D | 0 | 0.40 |
| E | 0 | 0.30 |
AUC 的意思是:隨機抽「一個正類(會定存)」和「一個負類(不會定存)」各一個,看模型有沒有把正類排在負類前面;做很多次,勝率就是 AUC。
這裡正類有 2 個(A、B),負類有 3 個(C、D、E)。所有「正對負」配對一共有 2 * 3=6 組:
贏了 5 次 / 總共 6 次 = AUC = 0.833。
這就是「排序能力」的白話:模型有 83.3% 的機率把真的會定存的人排在不會定存的人前面。
今天的重點
用 ROC 曲線看「閾值改來改去」時 TPR / FPR 的變化。
AUC = 排序能力:把正樣本整體排在負樣本前面的機率。
明天要做什麼
