分散式資料庫（e.g Cassandra、MongoDB）中的資料庫數量是可控的，Sharding Metadata 可儲存在外部資料庫 (e.g ZooKeeper) 或者儲存在所有叢集中的資料庫，讓 Client 能夠定位資料所在的資料庫。

但在去中心化的分散式儲存系統中，（如區塊鏈、IPFS、BitTorrent），情況變得截然不同：

• 節點分佈全球：任何人都能隨時加入或離開網路
• 完全去中心化：沒有中心化的伺服器或協調節點
• 動態拓撲：節點數量和網路結構持續變化
• 連線限制：單一節點無法與所有其他節點建立連線

這些特性使得的 Sharding Metadata 管理方式變得更複雜，例如：

• 叢集中節點無法與所有其他節點建立連線，因此無法建立完整的 Sharding Metadata
• 無法依賴中心化的服務 (e.g zookeeper) 來儲存 Sharding Metadata

那麼去中心化儲存系統如何維護 Sharding Metadata 幫助 Client 定位資料所在的資料庫位置？

參考網際網路的封包傳送機制，每個路由器 (Router) 只記錄如何到達鄰近區網，透過封包轉發的方式，多次跳轉最後抵達目的地。以此類推，在去中心化儲存系統中每個資料節點也只儲存鄰近節點資訊，不斷轉發請求給相鄰且最靠近目標資料的節點，最終找到資料的儲存位置。

但該如何定義節點和資料之間的「距離」和節點之間的「鄰近關係」?

此時就要用 Distributed Hash Table (DHT) 技術，DHT 包含:

• 基於距離的 Data Sharding 策略：透過計算資料與儲存節點的距離來分配資料，距離越短代表該資料越可能被分配到該節點。
• Routing Table 結構：每個節點只與特定的「重要鄰居」建立連接，透過 Routing Table 轉發讀取請求給最靠近資料的儲存節點。

例如 Consistent Hashing 就是有距離的 Data Sharding 算法，在環中，儲存節點跟資料透過 Hash Function 獲得數字編號 (0~2³²-1)，環中順時針距離就是資料距離，例如 1 到 10 的距離比 1 到 200 短，1 到 0 的距離比 1 到 3 來得長。

而儲存節點只儲存順時針的下一個節點當作 Routing Table 即可，資料不存在時，只需往下一個節點轉發，不斷往前定能找到資料的所在資料庫。

但這樣跳轉的效率很差，最壞情況會到 O(N) 的跳轉次數，因此如何建構高效的 Routing Table 就是 DHT 的設計關鍵！

Chord DHT 如何高效地定位資料的資料庫位置？

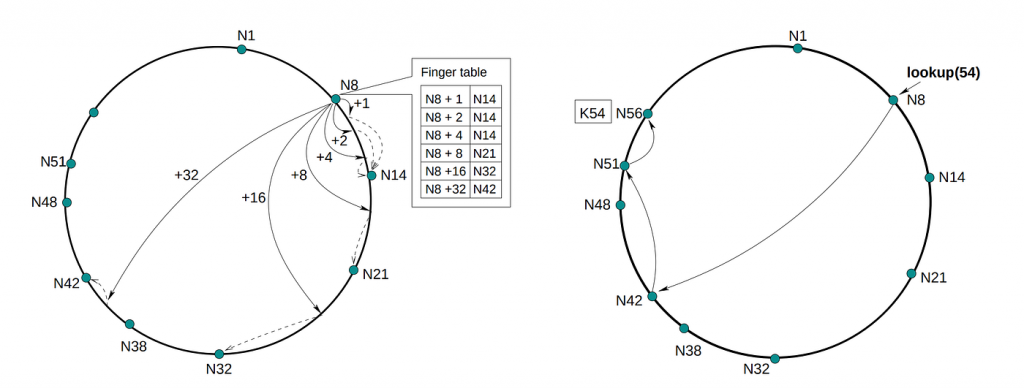
Chord 是基於 Consistent Hashing 但具備更高效路由表的 DHT 結構，其跳轉次數在最壞情況下可達到 O(log N)。

Chord 的 Routing Table (aka Finger Table) 會紀錄距離為 2^i 的相鄰節點，假設 Consistent Hash 是一個 0~63 的環，資料節點分別位於 1, 5, 12, 25, 38，那麼節點 1 的 Routing Table 為：

finger[0] = successor(1 + 2^0) => 大於等於 2 的第一個節點 => 5  
finger[1] = successor(1 + 2^1) => 大於等於 3 的第一個節點 => 5  
finger[2] = successor(1 + 2^2) => 大於等於 5 的第一個節點 => 5  
finger[3] = successor(1 + 2^3) => 大於等於 9 的第一個節點 => 12  
finger[4] = successor(1 + 2^4) => 大於等於 17 的第一個節點 => 25  
finger[5] = successor(1 + 2^5) => 大於等於 33 的第一個節點 => 38

查找資料的流程為：

1. 檢查資料的 sharding key 是否位於自己跟 finger[0] 的節點之間，如果是資料就位於 finger[0]
2. 如果不是跳轉到節點編號小於 sharding key 的最大節點
3. 重複 step 1 & step2 直到找到資料位置

例如 sharding key 為 30，從節點 1 開始會先跳轉到節點 25，到節點 25 後，因為 30 位於 25 跟 25 的 finger[0] (successor(25+2⁰) 節點 38) 之間，所以資料就位於 38 節點中，總共跳轉 2 次。

假設環的大小為 2^m，那麼 routing table 的長度最多就是 m，也就是最多跳轉 m 次，當 n = 2^m 時，m 就等於 logN，因此跳轉次數為 O(logN)。

(圖來源：https://medium.com/princeton-systems-course/chord-dht-in-python-b8b8985cb80e)

但 Ethereum、IPFS、BitTorrent 卻是用 Kademlia DHT，為什麼？

儘管 Chord 有 O(log N) 複雜度，但 IPFS、BitTorrent 及 Ethereum 等主流系統卻採用 Kademlia DHT，原因是 Chord 的跳轉路線像是一條筆直的道路，每次跳轉節點只有一個選擇，如果下一個跳轉節點出問題就必須採用效率較低的替代路徑。

而 Kademlia 就像一個網狀的道路，如果前面路口被封住，還可以轉彎換一條道路，具備優秀的路由冗餘特性。

Kademlia 使用 XOR 計算距離，XOR 算出的數字越大代表距離越遠，將資料範圍定義在 0~2⁶⁴-1，最遠距離就是 0 XOR 2⁶⁴-1 等於 2⁶⁴-1，不像 Consistent Hashing 是順時針距離要處理 2⁶⁴-1 尾巴節點下一個為 0 的例外情況，XOR 距離計算相較單純。

另外 Kademlia Sharding 不像 Consistent Hashing 只能將資料放在順時針的下一個節點，我們可以定義一個距離的 Threshold，例如距離小於 5 的節點都存放資料，資料備份在多節點可用性高。

Kademlia 的 Routing Table (aka K-Bucket ) 跟 Chord 類似，一樣採用 2 的 n 次方距離，但不同的是，一個 2^i 距離會有多個節點，以此形成網狀道路，創造路由冗餘。

例如假設節點為 1 其 Routing Table 為

K-Bucket[0] : 距離在 2^0 ~ 2^1-1 之間的節點都在該 bucket：2  
K-Bucket[1] : 距離在 2^1 ~ 2^2-1 之間的節點都在該 bucket：3  
K-Bucket[2] : 距離在 2^2 ~ 2^3-1 之間的節點都在該 bucket：4,5,6,7  
K-Bucket[3] : 距離在 2^3 ~ 2^4-1 之間的節點都在該 bucket：8,9,10,11,12,13,14,15  
.....

查找邏輯為：

1. 節點 ID 跟資料 sharding key 做 XOR 算距離
2. 找出距離位於哪個 K-Bucket 範圍，例如 1010 XOR 1101 = 0111 = 7，7 位於 K-Bucket[2] (i.e 距離 4, 7 之間)
3. 從該 K-Bucket 中所有的相鄰節點，並行執行跳轉
4. 重複上述步驟
5. 直到找到資料或者距離等於 0 或小於 Threshold

由於 Routing Table 的長度也是 logN，所以 Kademlia 最多跳轉次數也是 O(logN)，但相較於 Chord 其網狀路由特性，支援資料備份和多路由選擇，能提升整個去中心化網路的韌性。

(圖來源：https://medium.com/@vmandke/kademlia-89142a8c2627)

Ethereum 為何需要使用 Kademlia？

Ethereum 中所有節點都要具備完整資料，不需要 data sharding，因此 Kademlia DHT 主要用於節點發現，而不是分散儲存資料。

但為何不能隨機連上 N 個節點就好？需要 Kademlia DHT？

隨機連 N 個節點可能造成網路分割，無法保證全網覆蓋，例如節點 A,B,C 互連，E,F,G 互連形成兩個群體，造成區塊鏈分叉，新節點無法廣播給所有人，共識遭到破壞，而透過 Kademlia 的節點距離規則，能建立盡可能分散的網路。

假設美國的節點 ID 都集中在 0x0000... ~ 0x7FFF... 段落， 而歐洲節點 ID 都集中在 0x8000... ~ 0xFFFF... 段落， 依照 Kademlia 的 Routing Table，每個節點會在不同距離範圍建立連結： - 近距離 bucket：連接同區域節點，美國連美國，歐洲連歐洲 - 遠距離 bucket：連結不同區域節點，美國連歐洲，歐洲連美國網路覆蓋高，能高效地廣播新區塊給所有節點。不過實際上節點 ID 是加密雜湊隨機生成的，與地理位置無關， 但 Kademlia 的結構化設計仍可達到類似的全網覆蓋效果。