昨天我們聊了神經元的本質，知道它能做「輸入 → 加權 → 激活 → 輸出」。
但單顆神經元的能力其實很有限，今天我們要把神經元一顆顆疊起來，看看這樣的網路能帶來什麼力量！

一、為什麼要多層？

單顆神經元（感知器）的能力有限，只能處理「線性可分」的問題，例如用一條直線把資料分成左右兩類，但像經典的 XOR（互斥或）問題就無法解決；而當神經元堆疊成多層時，網路便能捕捉到更複雜的非線性邊界，層數越多，所學到的特徵也越抽象：第一層可能只辨識邊緣或簡單模式，第二層能組合成形狀，第三層甚至能識別更高階的物件。

二、神經網路的架構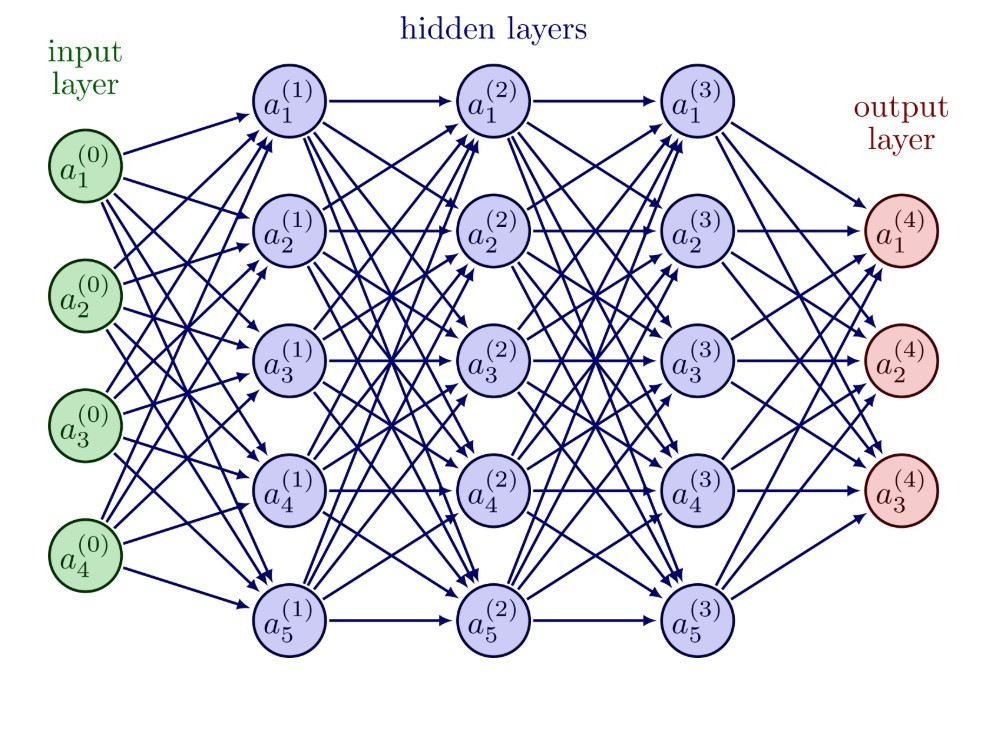

資料來源: https://tikz.net/neural_networks/

一個基本的神經網路通常包含三種層次：

輸入層 (Input Layer)：接收資料（例如圖片的像素、數值特徵）

隱藏層 (Hidden Layers)：真正的「黑箱」，負責提取與轉換特徵

輸出層 (Output Layer)：產生最終結果（例如貓 / 狗、0~9 數字）

三、初始化的重要性

不過，把神經元疊起來並不是「隨便堆」就行。
如果一開始所有權重都設成一樣，神經元就會「學同一件事」，網路就沒用了。

為了解決這個問題，研究者提出了不同的初始化方法：

Xavier 初始化：適合 Sigmoid / tanh
He 初始化：適合 ReLU

初始化為什麼重要？

如果我們隨便把權重設太大，輸入經過多層相乘相加，數值可能爆掉（梯度爆炸）；
如果設太小，又可能在多層傳遞後變成接近 0（梯度消失）。

👉 結果就是：網路不是學不起來，就是收斂超慢。

因此，好的初始化方法會根據激活函數的特性，把初始權重設在「剛好合適」的範圍，
讓訊號能穩定地往前傳、誤差能穩定地往後傳。

Xavier 初始化（Glorot Initialization）

• 適用激活：Sigmoid、tanh

• 想法：希望每一層的輸入與輸出「變異數差不多」，不會一層層越傳越大或越小。

• 公式：

  權重 ( W ) 的範圍來自均勻分佈：
  

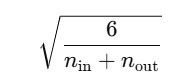
的均勻分佈。這樣能讓訊號在 Sigmoid/tanh 激活下不會馬上飽和（卡在 0 或 1），梯度才不會消失。

就像把角色屬性分配得「均衡」，不會一開始力量點滿結果智力完全空白。

• 適用激活：ReLU 與其變體（Leaky ReLU、ELU）

• 想法：因為 ReLU 會把一半輸入「截斷成 0」，如果用 Xavier，輸出的變異數會縮水。
  所以 He 初始化會放大權重範圍，確保輸出訊號的變異數仍然夠大。

• 公式：

  權重 ( W ) 的範圍：
  

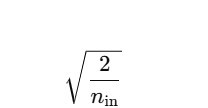
作為分佈範圍。適合 ReLU，因為它天生會丟掉一半訊號，需要「加強火力」才不會弱化。

就像角色天生有「半血設定」（ReLU < 0 的訊號直接歸零），
那就得一開始給他多一點力量點數，才能打得過怪。

這就像遊戲裡的「角色初始屬性分配」。如果一開始點錯技能，角色後面會卡關；好的初始化能讓模型更快更穩地成長。