條件機率

那我就先幫大家複習一下條件機率吧！
條件機率是指在某些條件發生的前提之下，某件事發生的機率，其實人類觀察很多事物是用條件機率做判斷的，而非一般的機率。
即使我們知道癌症發生的機率已經因為人類醫療的發達大幅降低了許多，但是對於被檢驗出可能得癌症的人跟檢驗出沒有得癌症的人，兩者的風險是大大的不相同的。

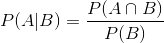
以上這個式子說明了條件機率的定義，他的意思是，在B發生的前提下，A發生的機率是多少。
我認為英文在表達上更簡易貼切，其中的直線的符號是given的意思，也就是probability of A given B，在給予B發生的情況下，A發生的機率。

也就當給予了愈多的資訊，判定其實會愈準確的意思。
像是我今天敘述

有個學生走在放學回家的路上。

這時候在腦中浮現的景象是什麼？你可能會推論，現在是放學時間、學生穿著校服、背著書包等等。
當我給予更多的資訊...

有個學生拎著書包輕快地走在放學回家的路上。

喔？原來他是拎著書包的！跟我的想像不一樣！
這就是給予的資訊程度不同，判定的準確度會不同的意思。

貝式定理

接著我們進到貝式定理，貝式定理再說些什麼呢？其實如果光看公式定義上面寫著A跟B，你大概猜不到數學家原本設計這東西出來是要做什麼的。
我把他轉成以下這個樣子或許比較好懂。

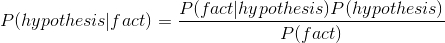
其實我們要估計的是給定某個事實（fact），模型或是假說（hypothesis）為真的機率有多高。
所以當你看到把公式展開，分子的部份有兩個：

1. P(fact|hypothesis)意思是假設某個假說是對的，那我手上的資料有多麼符合這個假說，也就是可能性的意思
2. P(fact)這邊代表的是先驗機率(prior probability)，這個地方比較特別，他需要你把預先知道的知識放進去一起估計

分母的部份指的就是模型或假說的機率拉~~~什麼叫作模型或假說的機率！
其他他只是為了將機率的分佈調成總和為1而已，因為分子計算出來他的總和不保證是1，所以需要做校正。

雖然高中的老師都會叫我們畫出樹狀圖，以方便計算，不過我們這邊沒有要強調計算就秀一下就好。

貝式定理的概念可以進一步把他轉成以下這個樣子呈現

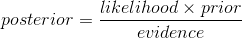
我們就可以得出所謂的後驗機率(posterior probability)，貝式定理的運算主要來自兩個重要的東西，一個是資料，我們會根據資料是否符合模型或假說來估計出所謂的likelihood function，另一個就是先驗機率，也就是在看過資料之前，你對你要推論的東西知道多少。
換句話說，資料跟預先的認知對貝式推論來說是重要的，跟只看資料跟模型的吻合程度的傳統機率不一樣，以上就是貝式定理的概念了！

貝式推論框架

到這邊大家應該都對貝式定理有些了解，那他要怎麼拿來做推論呢？

跟傳統統計推論一樣需要有個假說，但是這個假說不是非黑即白的，不是null hypothesis、alternative hypothesis。

假設現在有個袋子，當中有各種顏色的球，我想知道其中黃色的球的比例是多少。
那我會假設很多個假說：H1: 10%, H2: 20%, H3: 30%..., H9: 90%
接下來建立先驗機率，由於我對於袋子裡的球一無所知，所以我就假設H1~H9發生的機率是平均分佈好了，也就是每個假說都有1/9的機會，當然如果你覺得哪個比率比較高你可以做調整。
然後抽樣，我從袋子當中抽出5個球，其中一顆是黃色。

接下來計算likelihood，這裡會利用二項分佈去計算

P(抽出一顆黃色|H1成立) = C5取1 * 0.1 * 0.9^4 = 0.32805
P(抽出一顆黃色|H2成立) = C5取1 * 0.2 * 0.8^4 = 0.4096
....
P(抽出一顆黃色|H9成立) = C5取1 * 0.9 * 0.1^4 = 0.00045

最後的後驗機率就是

P(H1成立|抽出一顆黃色) = (0.32805 * 1/9) / 各項分子的總和
.....

最後在從後驗機率中選出最大的當作推論結果。

下一篇會比較這兩種觀點的機率