在正式進入本篇之前, 先來複習國中數學一元一次方程式與一元二次方程式, 一元一次方程式為y=aX+b, 在平面座標顯示為一直線範例如下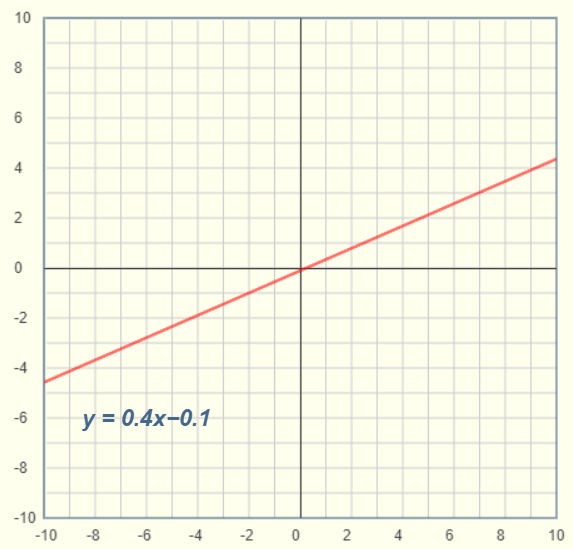

而一元二次方程式為y=aX^2+bX+c, 在平面座標顯示為曲線範例如下

而X到X^2, 可以發現從直線到畫出曲線了, 接著再來改寫式子如下

y=aX+b -> y=b0+b1X (Simple Linear Regression, 統計學稱簡易線性回歸)

y=aX^2+bX+c -> y=b0+b1X+b2X^2 (Polynomial Regression, 統計學稱多項式回歸),

這邊就不解釋統計學上簡易線性回歸與多項式回歸的進階公式推導如SSR, SSE, SST與MSE等, 有興趣的朋友可以翻一下統計學的書籍. 這邊單純把統計學的名詞跟國中的數學做一個呼應, 而以簡易線性回歸而言, 機器學習的重點在於利用電腦運算去找出最佳的一條線的方程式, 以國中學過的名詞來說, 就是找出最佳斜率, 以統計的角度來說就是找出b0,b1等係數即所謂Coefficient(變異係數), 接下來拿底下簡單的範例來練練手.

某日, 公司的HR主管帶著薪資職位核薪表來找你, 希望你可以開發一個系統來預測面試人員所要求的薪資與職位是否合乎預期?或是核薪是否合理? 薪資職位核薪表資料下: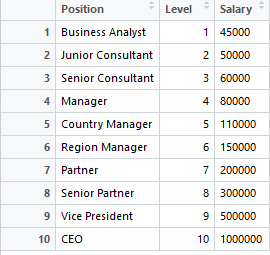

以簡易線性回歸的式子來看就是 薪水 = b0 + b1 * 職等, 我們希望透過上述的資料, 用電腦幫我們找最佳b0與b1, 所以接下來就開始寫程式囉, 先把資料讀近來, 順便取出所需的Level與 Salary, 透過plot方式觀察資料間是否有甚麼特性?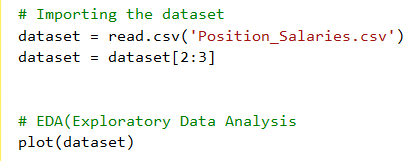


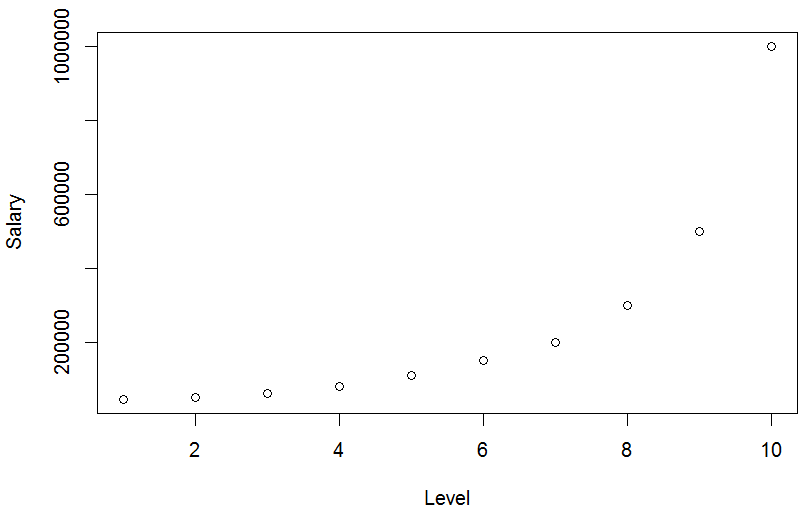
由上圖可以觀察到當Level越大, Salary也越大, 接著試著跑一下Simple Linear Regression, 並且利用跑出來的結果作預測如下

dataset$pred為預測的結果, 接著將dataset叫出來看一下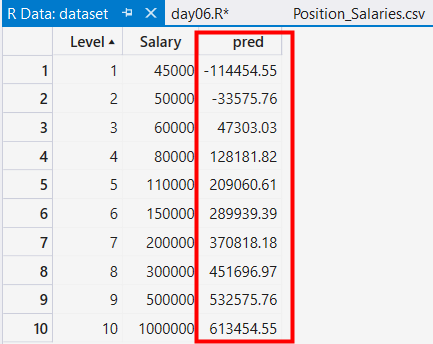

應該有人會好奇, 這是如何預測出來的? 可以在Variable Explorer點擊lreg, 就會看到前面提過的Coefficient(變異係數)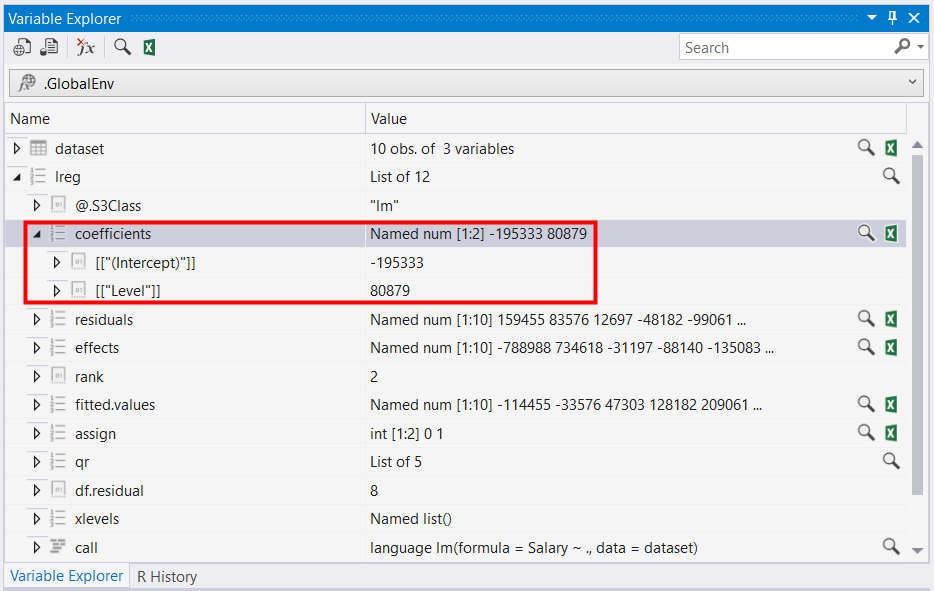

還記得之前提的簡易線性回歸式子:薪水 = b0 + b1 * 職等 即pred =b0 +b1 * Level,而套上Coefficient, 變為底下式子

pred =-195333 + 80879 * Level

然後我們把Level=1 帶入

pred =-195333 + 80879 * 1=-114454

Bingo! 原來是這樣算出來的

接著我們來評估預測結果, 實際值與預測值做一個相除, 其值愈接近1, 代表預測愈準確

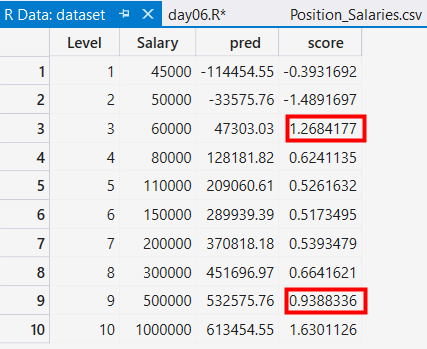
結果只有Level =3 與 Level =9比較接近1而已, 下一個步驟就是把這個結果視覺化出來, 我們用ggplot2來繪圖如下

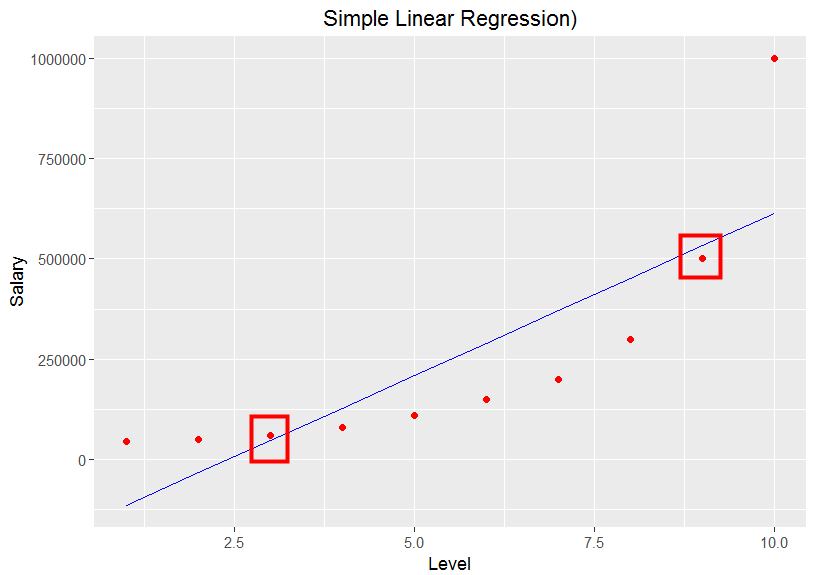
由上圖可以發現Level =3 與 Level =9比較貼近算出來的這條線, 其餘的離得比較遠, 而這種情形就稱之為Under fitting, 這種現象就是代表所用的模型, 非常不準即Performance不好, 而這也是在機器學習裡, 想解決的情況之一.

本篇完整程式碼如下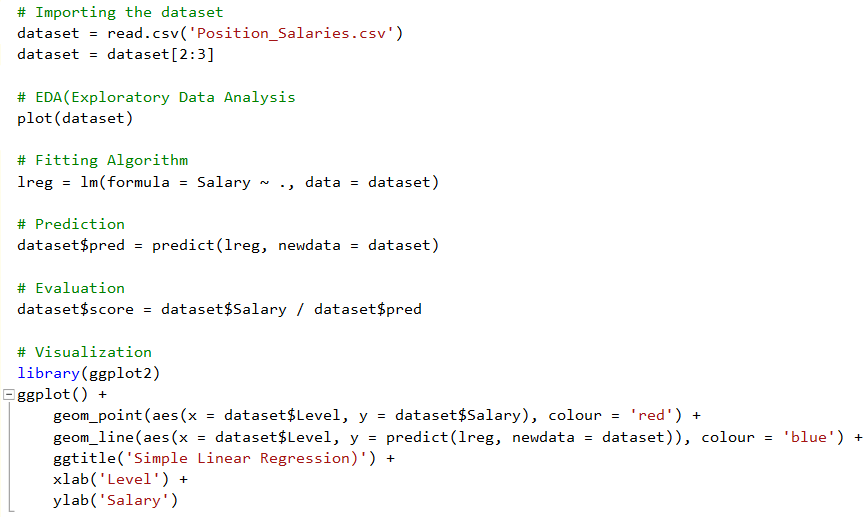

本文參考
Udemy Machine Learning A-Z™ Hands-On Python & R In Data Science-04.Simple Linear Regression
http://www.superdatascience.com/wp-content/uploads/2017/02/Simple_Linear_Regression.zip