接續上一篇的結論, y=b0+b1X的預測效果不是很好, 甚至Under fitting了, 所以回到EDA的步驟, 試著把所有點連起看看, 修改程式碼如下


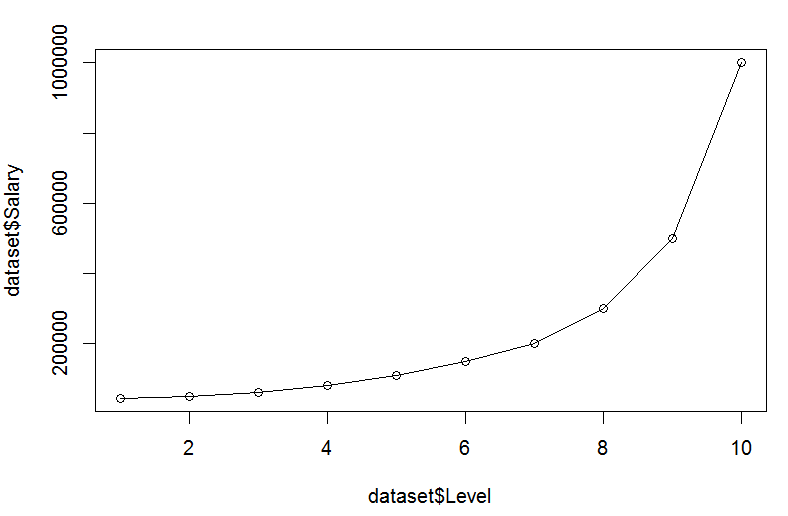
觀察上圖後發現, 好像一條曲線而非直線, 所以應該可以用y=b0+b1X +b2X^2來試試, 由上一篇了解到X指的是職等即Level, 所以我們可以新增一個X^2的資料, 即加入Level平方的資料進來, 修改程式碼如下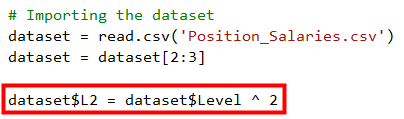

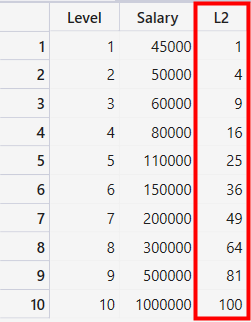
接著在# Fitting Algorithm步驟新增lreg2, Prediction步驟新增pred2, 作為預測結果, 程式碼修改如下:

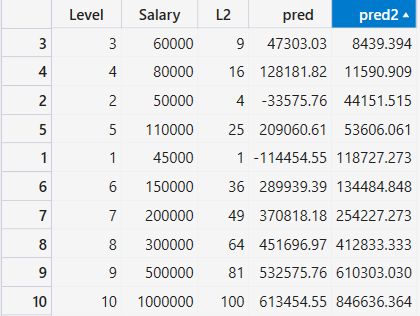
觀察一下pred2的預測結果, 似乎比pred好一些, 接著一樣在Evaluation步驟加入score2, 比較看看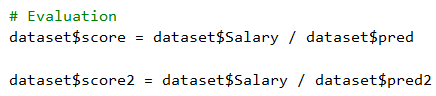

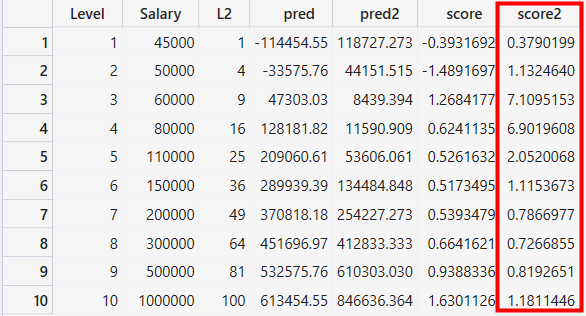
score2似乎比score準確一點, 接著一樣來透過ggplot2做視覺化如下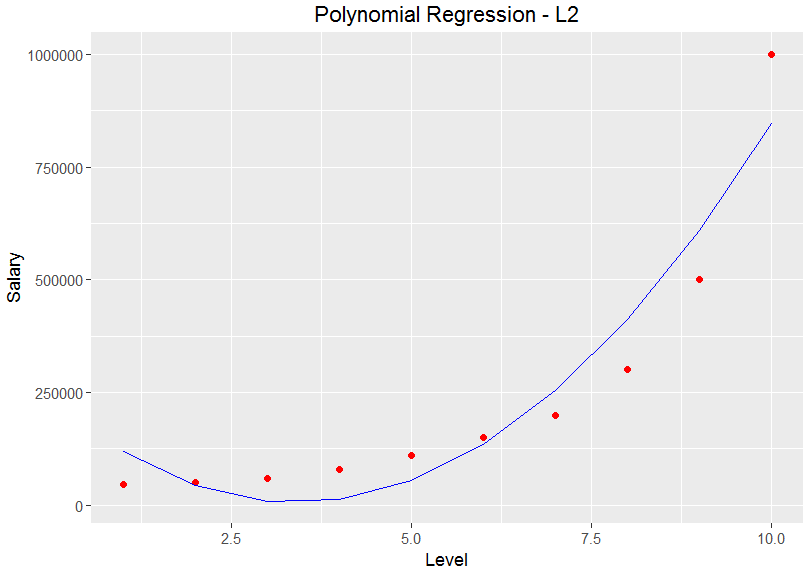

看起來好像有點樣子了, 來修改一下程式碼, 把前一篇的圖也放進來比較

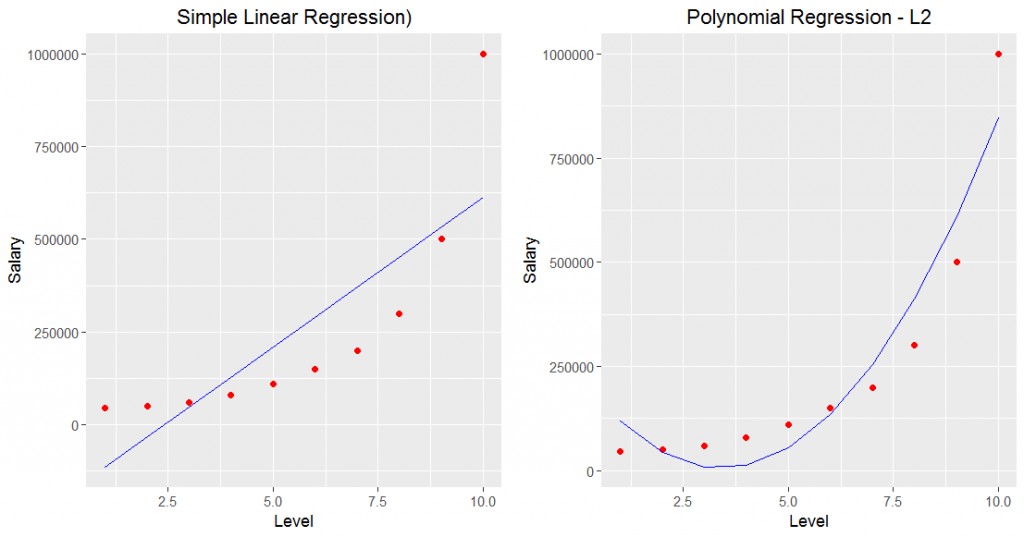
一比較後明顯進步了, 所以用多項式感覺有點用, 接著加入Level的三次方與四次方跑看看, 資料如下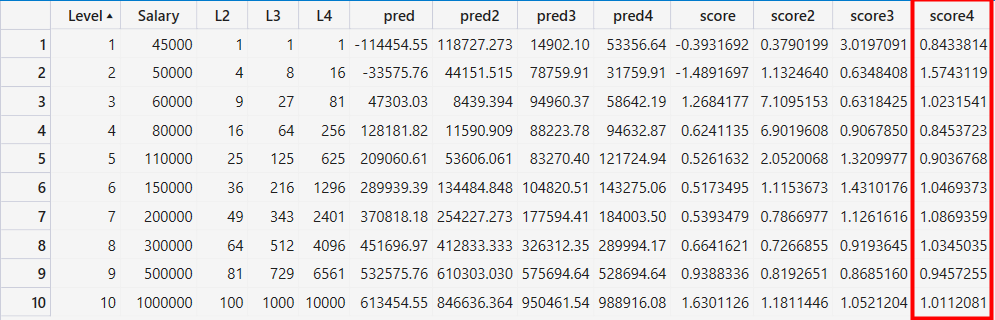

由上圖可知四次方的score4是4個裡面最準確的, 接著一樣把四個圖放在一起,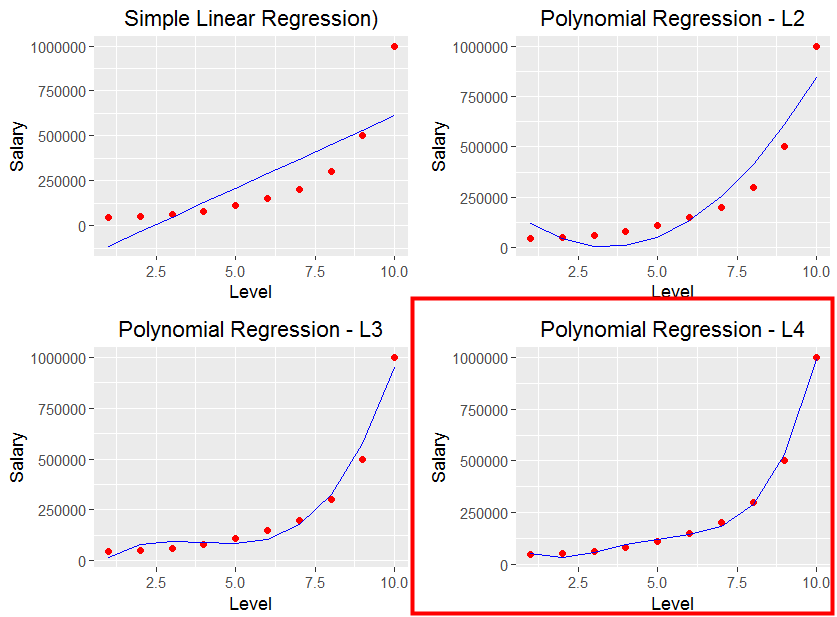

我們可以發現四次方的圖, 很完美將所有點串在一起, 而這就是所謂的Overfitting, 而Overfitting會造成的問題是在訓練資料時很準, 但是測試資料非常不準, 要如何解決? 透過下一篇來總結Under fitting與 Overfitting囉

本文參考
Udemy Machine Learning A-Z™ Hands-On Python & R In Data Science- 06.Polynomial Regression
http://www.superdatascience.com/wp-content/uploads/2017/02/Polynomial_Regression.zip