前言

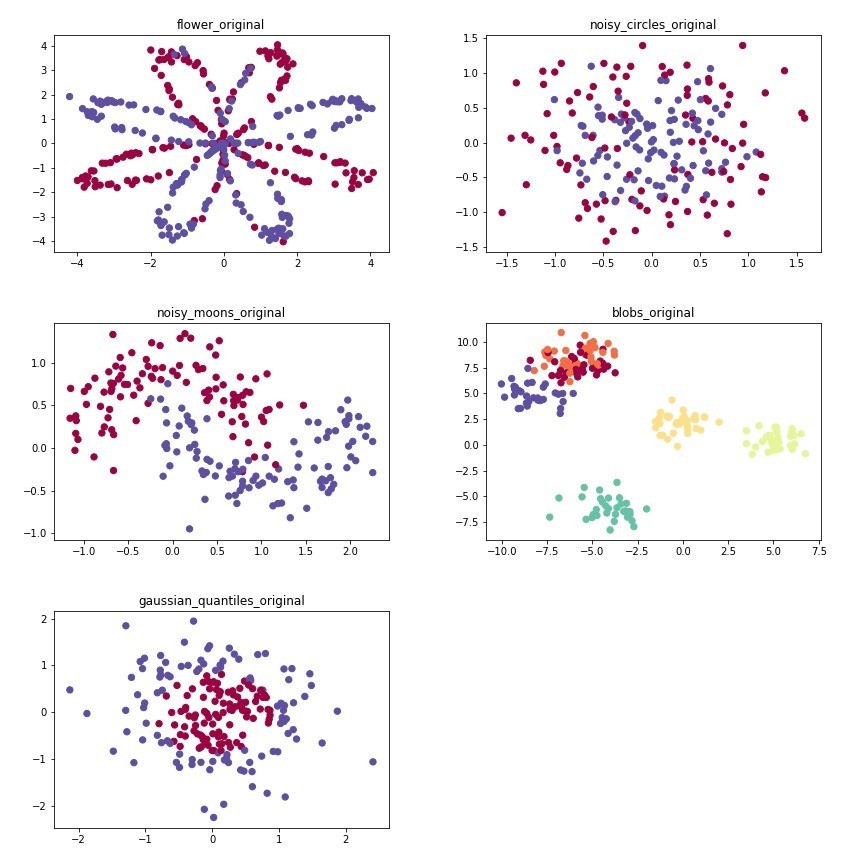
這篇文章將承襲上一篇文章，視覺化各個演算法的成果，並附註說明，讓大家更能夠了解，每個演算法運作的原理，及其用處。以下將用五個資料集，進行實測: flower, noisy_circles, noisy_moons, blobs, gaussian_quantiles。這原本是用來做分類的，所以紅色跟藍色就是他的類別，然後這個資料集為了方便視覺化，所以只設計出兩個維度。

Import

import matplotlib.pyplot as plt
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
import numpy as np
import os

from sklearn.cluster import KMeans
from sklearn.cluster import AgglomerativeClustering
from sklearn.cluster import DBSCAN
from collections import Counter

資料準備

X, Y = load_planar_dataset()
name = 'flower'
X = X.T
Y = Y[0]
plt.scatter(X[:, 0], X[:, 1], c=Y , s=40, cmap=plt.cm.Spectral);
plt.title(name+'_original')
plt.savefig(os.path.join('pic', name+'_original'))
plt.show()

noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {"noisy_circles": noisy_circles,
            "noisy_moons": noisy_moons,
            "blobs": blobs,
            "gaussian_quantiles": gaussian_quantiles}

datas = [(name, X, Y), ]
for name, dataset in datasets.items():
    X, Y = datasets[idx]
    datas.append((name, X, Y))
    
    print(X.shape)
    print(Y.shape)

    # Visualize the data
    plt.scatter(X[:, 0], X[:, 1], c=Y, s=40, cmap=plt.cm.Spectral)
    plt.title(name+'_original')
    plt.savefig(os.path.join('pic', name+'_original'))
    plt.show()

Flower

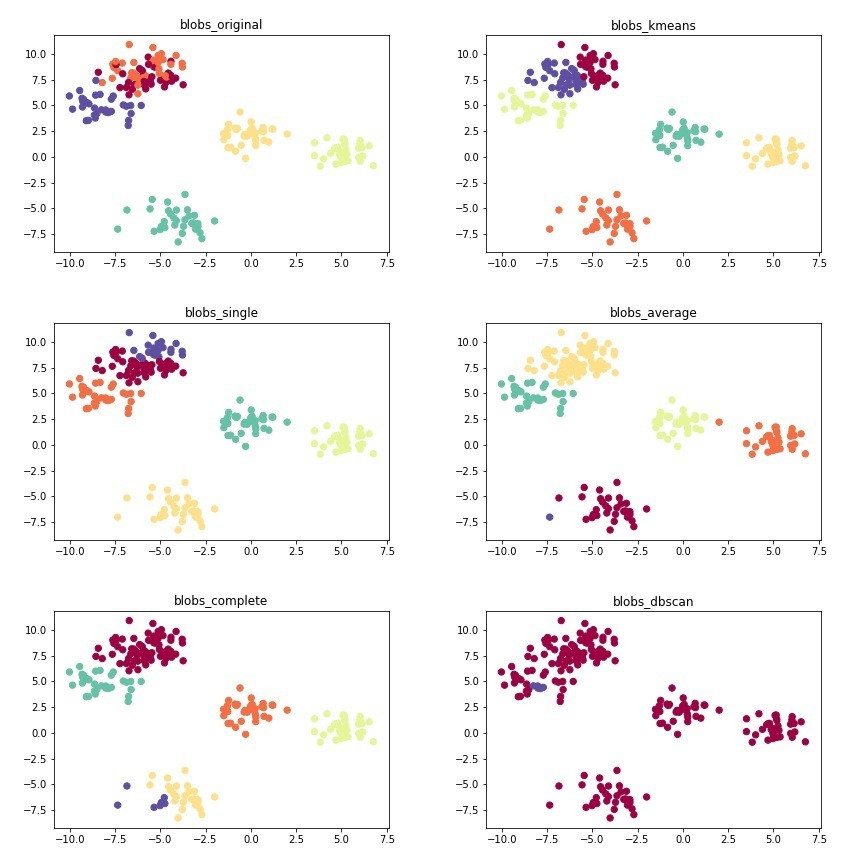
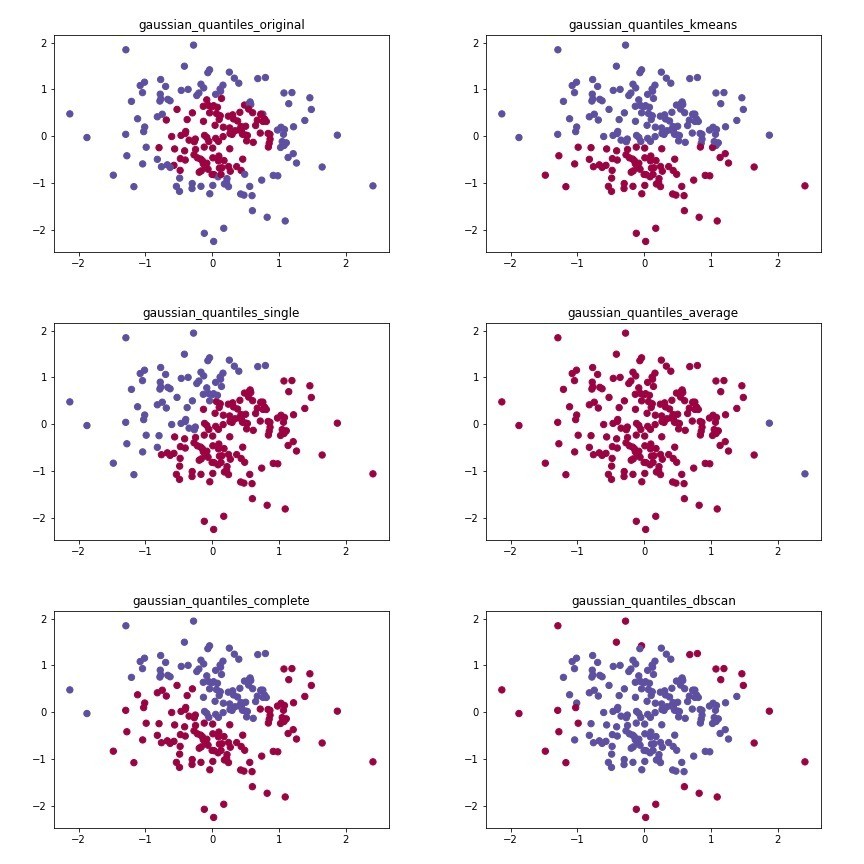
這張圖中，你們可以發現kmenas與hierarchical演算法的效果其實差不多，其實都是找比較相近的點，kmeans用比較有效率的方式找，hierarchical則是一群一群慢慢整併。dbscan則透過密度去尋找群組，可以設定eps的效果就不是特別好，因為dbscan比較常用來尋找極端值，而flower這張圖，很明顯不是一整群比較密集配上其他零星的小點，因此，密度比較高的自己就會被分成一群。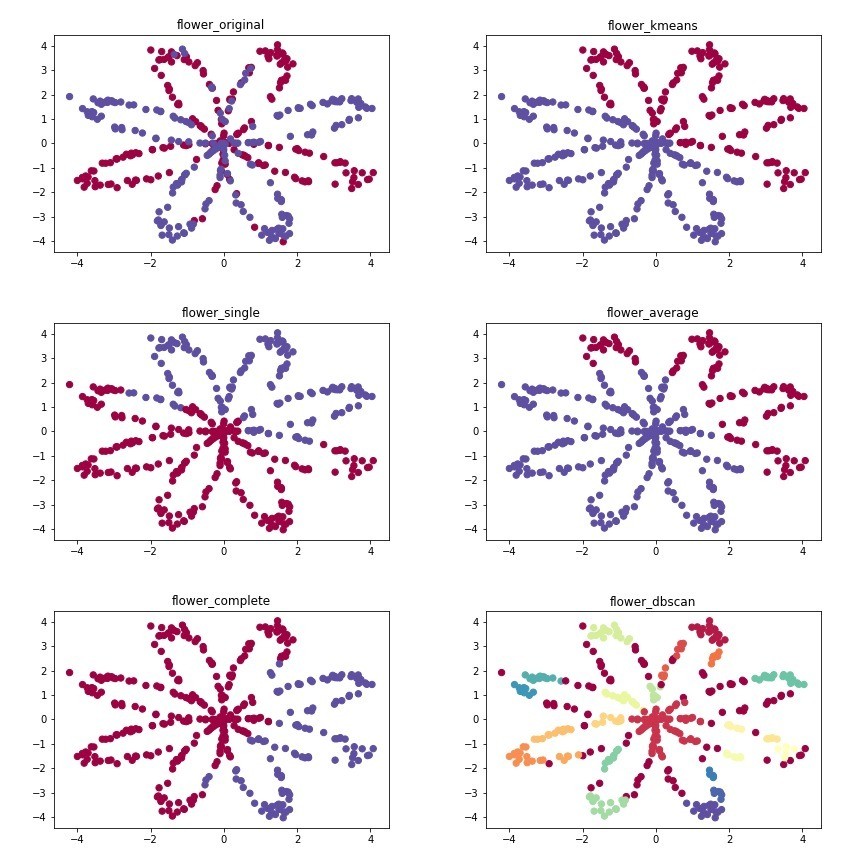

noisy_circles

這張圖來看，你就會發現dbscan的效果特別好，因為圓形內部的密度很高，而外部的點密度比較低，自然就會把密度高的分成一群。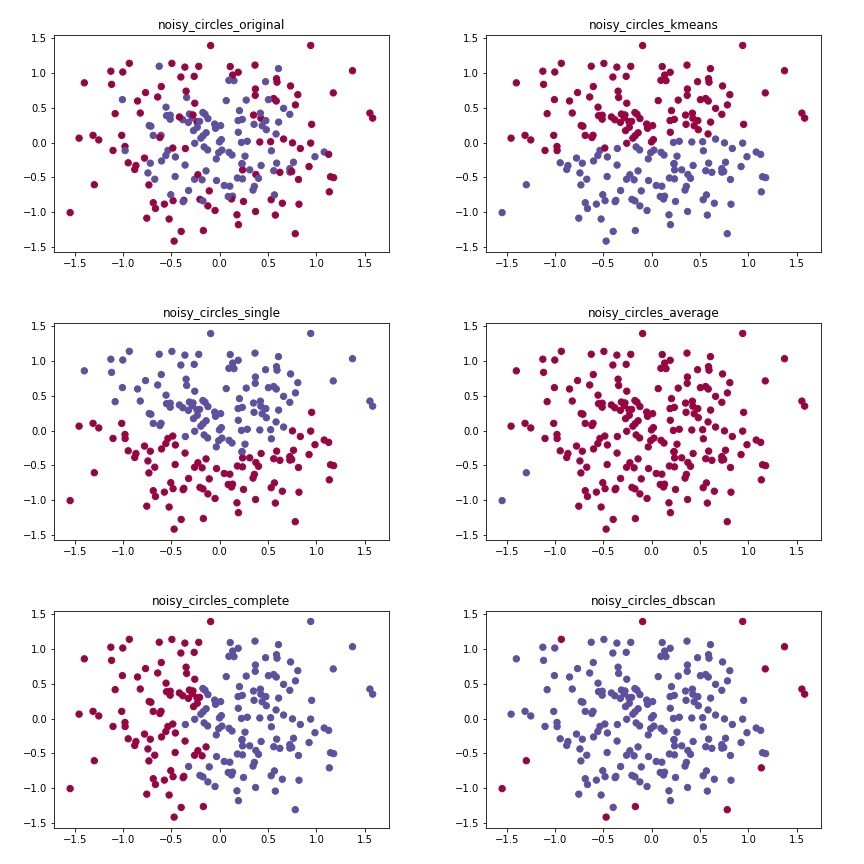

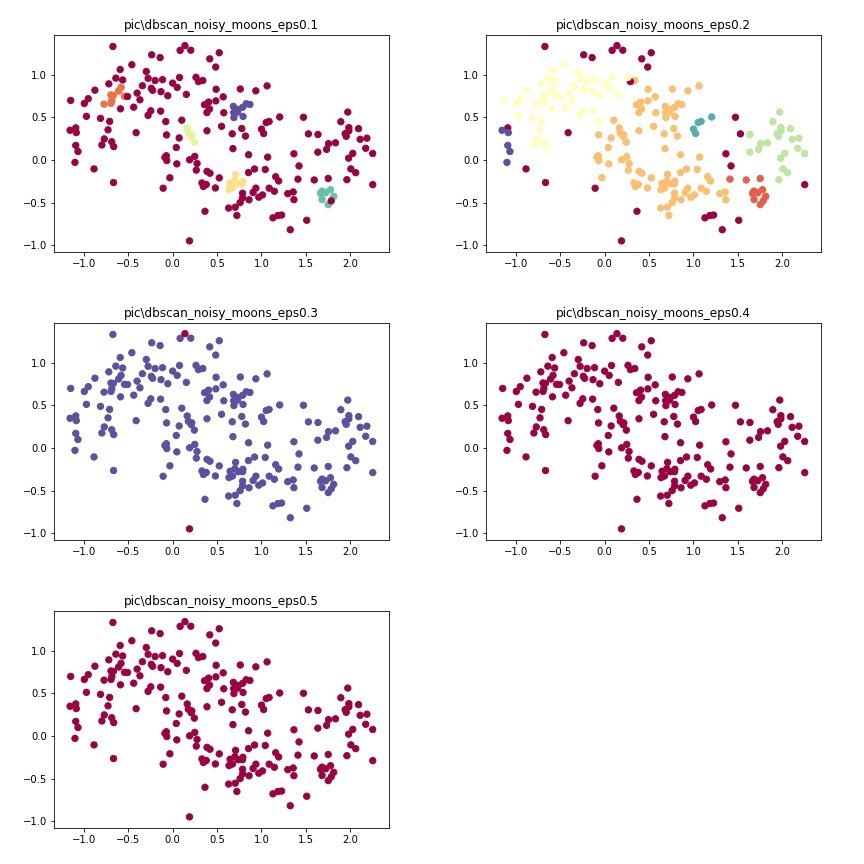
noisy_moons

blobs

gaussian_quantiles

不同eps的scan

大家會發現，在eps==0.2的時候，他的分群效果可以很明顯。如果要找極端值，eps設在0.3或0.4會比較剛好。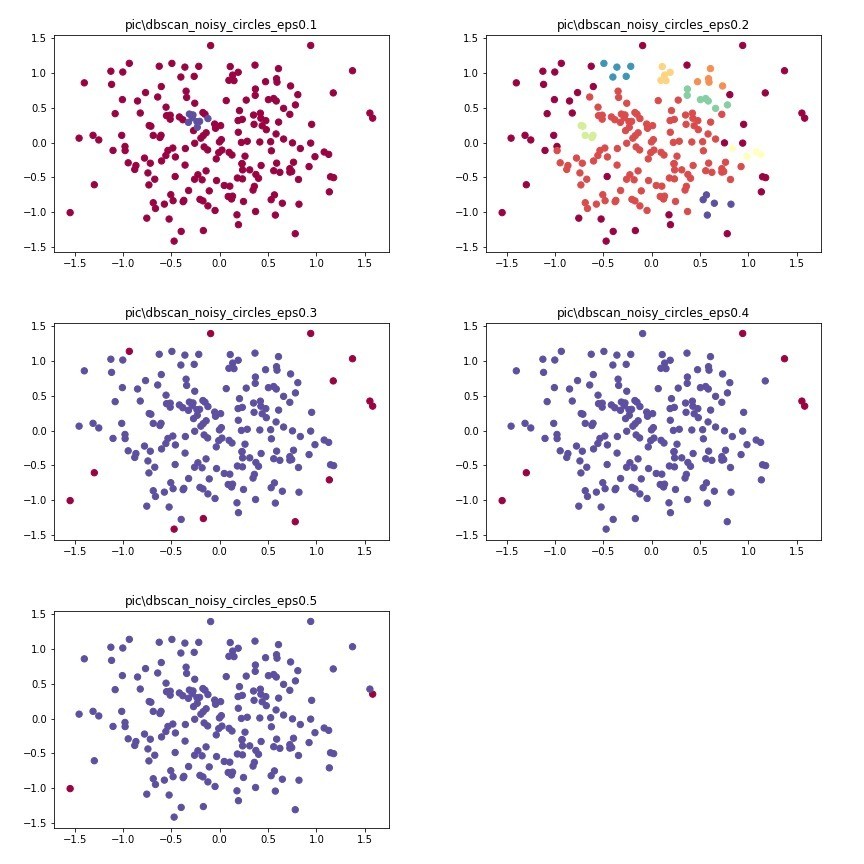

其他比較圖片的生產

# kmeans
for name, X, Y in datas:
    kmeans = KMeans(n_clusters=n_clusters, random_state=0).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=kmeans, s=40, cmap=plt.cm.Spectral);
    plt.title(name+'_kmeans')
    plt.savefig(os.path.join('pic', name+'_kmeans'))
    plt.show()
    
# hierarchical clustering: single link
linkage = ['ward', 'average', 'complete']
for name, X, Y in datas:
    hierarchy = AgglomerativeClustering(linkage=linkage[0], n_clusters=n_clusters).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=hierarchy, s=40, cmap=plt.cm.Spectral);
    plt.title(name+'_single')
    plt.savefig(os.path.join('pic', name+'_single'))
    plt.show()
    
# hierarchical clustering: average link
for name, X, Y in datas:
    n_clusters = len(set(Y))
    hierarchy = AgglomerativeClustering(linkage=linkage[1], n_clusters=n_clusters).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=hierarchy, s=40, cmap=plt.cm.Spectral)
    plt.title(name+'_average')
    plt.savefig(os.path.join('pic', name+'_average'))
    plt.show()
    
# hierarchical clustering: complete link
for name, X, Y in datas:
    n_clusters = len(set(Y))
    hierarchy = AgglomerativeClustering(linkage=linkage[2], n_clusters=n_clusters).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=hierarchy, s=40, cmap=plt.cm.Spectral);
    plt.title(name+'_complete')
    plt.savefig(os.path.join('pic', name+'_complete'))
    plt.show()
    
# dbscan
for name, X, Y in datas:
    n_clusters = len(set(Y))
    dbscan = DBSCAN(eps=0.3).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=dbscan, s=40, cmap=plt.cm.Spectral)
    plt.title(name+'_dbscan')
    plt.savefig(os.path.join('pic', name+'_dbscan'))
    plt.show()

code在這裡