今天想來跟大家分享泡沫排序法(Bubble Sort)，先來看一下維基百科的pseudo code：

function bubble_sort (array, length) {
    var i, j;
    for(i from 0 to length-1){
        for(j from 0 to length-1-i){
            if (array[j] > array[j+1])
                swap(array[j], array[j+1])
        }
    }
}

可以看到如果上面這樣排序的話，需要(n^2)的時間，但如果寫成電路的話，只需要O(n)時間，怎麼會這麼神奇呢，其實有點像是空間換取時間的感覺．

由於電路可以利用多個比較器，一次比較多個元素，有點像平行處理的感覺，所以只要發現能夠平行處理的資料，且在資源允許的情況下，當然希望能越快越好囉．

大概說明一下演算法，
有幾個元素就做幾個回合，所以需要一個counter計數回合，
單數回合做[0,1][2,3]…比較，如果大於就swap，
雙數回合做[1,2][3,4]…比較，如果大於就swap，
有幾個要比較的元素就比較幾個回合．

這邊簡單用一張圖說一下演算法:

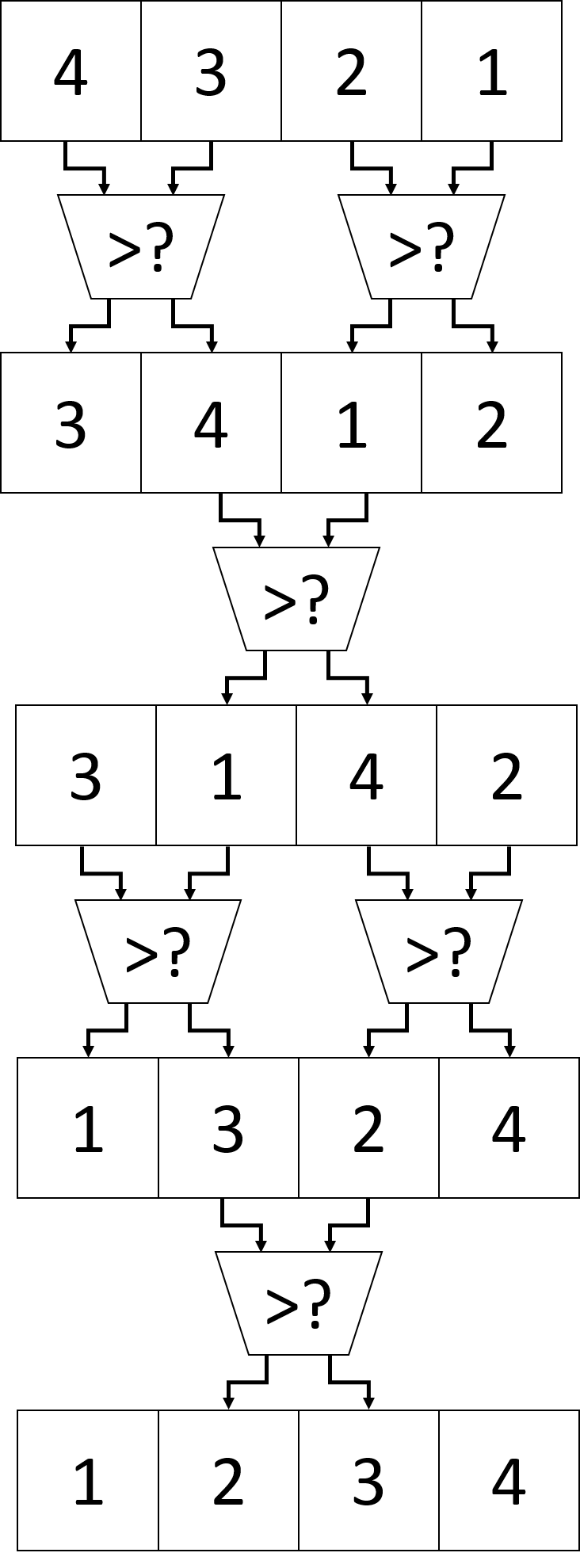
code：

assign out_valid = (sort_cnt == 4);

 always@(posedge clk)begin
         if(rst)
            sort_idx <= 0;
          else if(in_valid)
            sort_idx <= ~sort_idx;
       end
       

always@(posedge clk)begin
  if(rst)
  sort_cnt <= 0;
else if(in_valid)
  sort_cnt <= (sort_cnt == 4) ? sort_cnt : sort_cnt+1;
end

always@(posedge clk)begin
  if(in_valid & ~sort_idx)begin
    for(i=0;i<4;i=i+2)begin
      array[i  ] <= (array[i] > array[i+1]) ? array[i+1] : array[i  ];
      array[i+1] <= (array[i] > array[i+1]) ? array[i  ] : array[i+1];
    end
  end
  else if(in_valid & sort_idx)begin
    for(i=1;i<3;i=i+2)begin
      array[i  ] <= (array[i] > array[i+1]) ? array[i+1] : array[i  ];
      array[i+1] <= (array[i] > array[i+1]) ? array[i  ] : array[i+1];
    end
  end

波形：

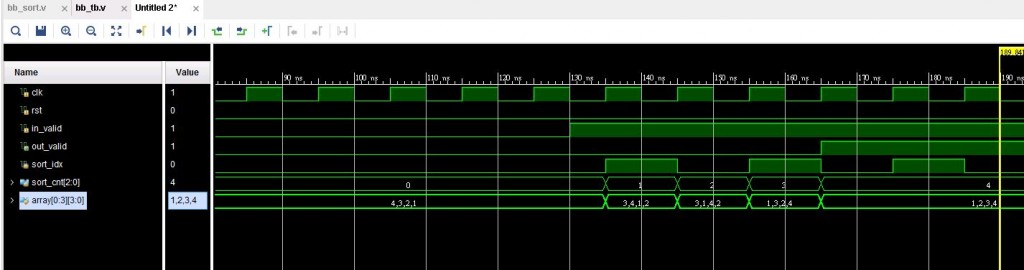
上面這張圖是做四個元素的排序，所以只需4個回合就能運算完，因為比較器能共用的關係，所以只要總元素除以2，這邊來說只需2個比較器即可，是不是跟想像中的泡沫排序有點不一樣呢，這就是電路有趣的部分，很多演算法只要發現規則，就會有不一樣的結果．