前言

昨天我們實作使用蒙地卡羅方法，進行狀態價值估計。不過昨天並沒有一口氣計算所有的狀態價值，因為獲得狀態價值這件事，在使用蒙地卡羅方法中，不是太重要的一件事。 (拜託不要打我) 以下我們將說明這件事：

狀態價值的意義

在「動態規劃」中

在動態規劃方法中，由原本的動作價值的定義：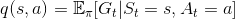

推廣為遞迴的形式：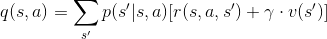

其中在計算動作價值函數時，需要使用狀態價值。因此，在動態規劃中，計算狀態價值是有意義的，因為它會影響後面計算動作價值。

在「蒙地卡羅」中

在蒙地卡羅方法中，並不是使用遞迴的形式求解，而是使用大量模擬實驗。

累積大量模擬數據後，取平均逼近價值函數，這個過程在我們昨天已經親身體驗過了。

雖然還沒有提到，但動作價值也是以大量模擬實驗的方式處理。所以，在蒙地卡羅方法中，我們其實用不到狀態價值。

取得動作價值

蒙地卡羅方法怎麼做？

昨天逼近狀態價值時，我們決定了

• 起始狀態
• 動作
• 回饋
• 轉移矩陣

並透過狀態價值的定義 ，估計 起始狀態 的價值。

在逼近動作價值時，也是類似的過程，不過這邊決定的參數有

• 起始狀態
• 起始動作
• 回饋
• 轉移矩陣

也就是說，我們在估計動作價值時，不只決定我們起始位置，連第一個動作也決定好了。舉個例子：

假設我們現在在狀態 1，我們要評估各動作的動作價值，那麼就會朝該動作移動一次後，再隨機動作。

• q(1, 上)：
  其移動流程為 1 > 1 > 隨機移動

• q(1, 下)：
  其移動流程為 1 > 5 > 隨機移動
  其中，最值得注意的是 q(1, 左)，這個動作在一開始移動後，就會抵達終點 (1 > 0)。在某種程度上，決定第一動，就造成移動到終點的難度差異。

與估計狀態價值相似，這邊計算動作價值時，也是直接根據動作價值函數定義：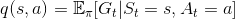

在上述例子中， q(1, 左) 的動作價值為 0 ，其餘情況則依其隨機移動情形而改變。

至此，我們了解蒙地卡羅方法計算價值的方式，明天我們將說明整體決策流程。