昨天介紹完SKlearn中的Feature Engineer，今天要來介紹貝氏分類器(Naive Bayes Classification)，該分類器模型在20世紀60年代初引入文本資料信息檢索中，文本資料分類的做法式將詞語出現的頻率用特徵值表示：

如果試圖在兩個標籤之間做出決策，可以利用類別1(L1)與類別2(L2)的方式計算出，並且可以計算出每個類別的都可以用此方式計算出比率：

貝氏分類器中的"naive"指的是，我們對每個標籤的生成模型做原是的假設，然後對模型中的每個類別做大約估計，不同類型的數據假設依賴於不同類型的貝氏分類器，首先匯入需要的函式庫和資料集。

Naive Bayes Classification

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

• 在貝氏分類器中，假設來自每個標籤的數據是從簡單的高斯分佈中提取的。

from sklearn.datasets import make_blobs
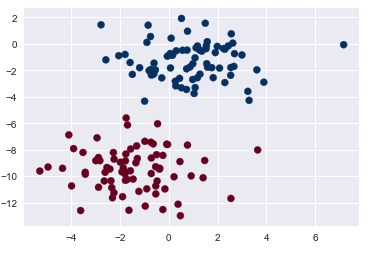
X, y = make_blobs(150, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu');

創建貝氏模型的一種非常快速的方法就是假設數據由高斯分佈描述，維度之間沒有平方差關係。只需找到每個標籤內各點的平均值和標準差即可擬合此模型，這就是定義這種分佈所需的全部內容：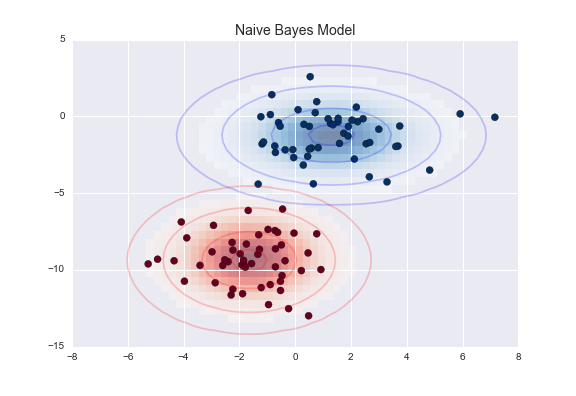

圖片引用：Python數據科學手冊/貝氏分類

上圖的橢圓表示每個標籤的高斯生成模型，朝向橢圓中心的機率值更大。有了這個每個類別的生成模型，我們有一個簡單的方法來計算任何數據點的類似於，因此我們可以快速計算後驗比率並確定哪個標籤給定點信賴值是最高的。

from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X, y);

• 生成一些新的數據並預設標籤

rng = np.random.RandomState(0)
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)
ynew = model.predict(Xnew)

• 再來繪製這些新數據，以了解決策邊界的位置：

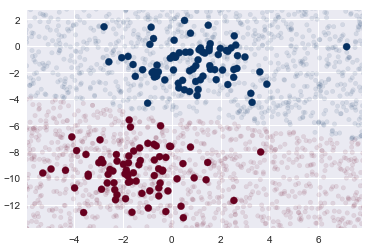
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
lim = plt.axis()
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='RdBu', alpha=0.1)
plt.axis(lim);

• 貝氏分類可以利用predict_proba()方法，簡單的做機率值分配

yprob = model.predict_proba(Xnew)
yprob[-8:].round(2)

Multinomial Naive Bayes

• 文本分類
  在sklearn中，匯入資料集fetch_20newsgroups，這個資料集有20個新聞的詞語，

from sklearn.datasets import fetch_20newsgroups

data = fetch_20newsgroups()
data.target_names

• 下載、訓練想要的資料集合類別

categories = ['talk.religion.misc', 'soc.religion.christian','sci.space', 'comp.graphics']
train = fetch_20newsgroups(subset='train', categories=categories)
test = fetch_20newsgroups(subset='test', categories=categories)
print(train.data[5])

• 為了讓這些數據可以適用於機器學習，因此，需要把每個字串轉換為數字向量(TF-IDF向量化)，TfidfVectorizer()

from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import make_pipeline

model = make_pipeline(TfidfVectorizer(), MultinomialNB())

• 再來，我們可以將應用於數據訓練模型，並預測測試數據的標籤

model.fit(train.data, train.target)
labels = model.predict(test.data)

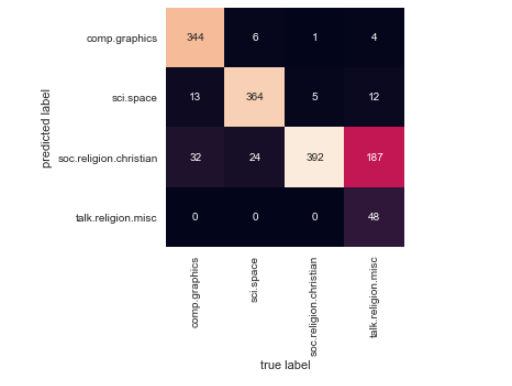
經過測試數據的標籤並對它們進行評估，以了解估算器的精確度。以下是測試數據的真實和預測標籤之間的混淆矩陣：

from sklearn.metrics import confusion_matrix
mat = confusion_matrix(test.target, labels)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False,
            xticklabels=train.target_names, yticklabels=train.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label');