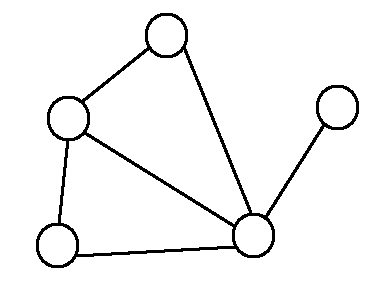
圖 (Graph),在資料結構上指的是點和點之間的關聯的東西,並不是數學定義上的兩點成一線,三點成一面的那種圖。一張圖由數條邊(Edge)和數個點(Vertex)所構成,點和點之間可用邊相連,表示這兩個點之間有所關聯。當然,兩個點之間可以有很多個邊,代表很多關係,又或者是一個點可以與很多個點相連接。
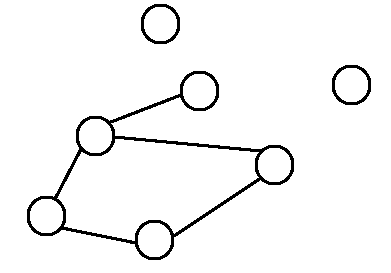
指的是兩張圖的連接方式一模一樣的,而圖上的點可以任意移動,邊不論直的彎的皆可。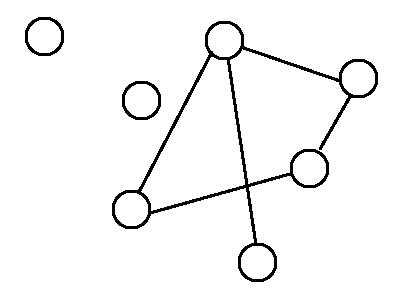
有向圖,邊有方向性,表示兩點之間為單向關係。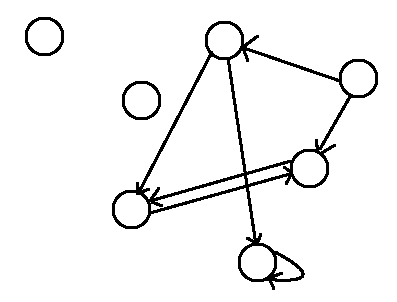
無向圖,邊無方向性,表示兩點之間為雙向關係。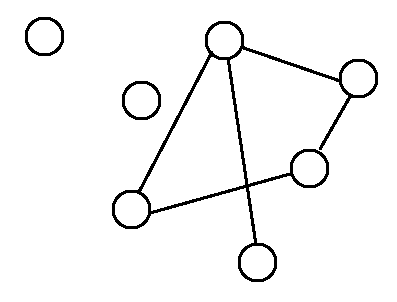
邊加上權重,代表兩點之間的關係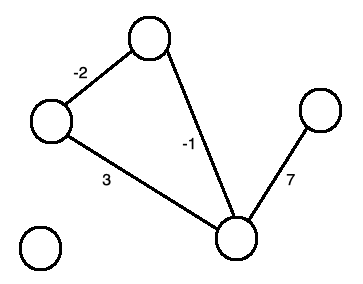
點加上權狀,代表狀態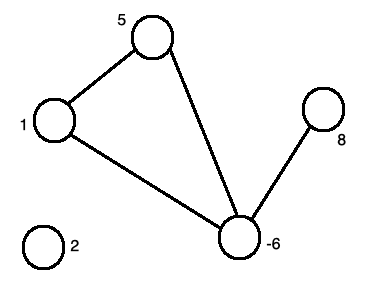
點可以有名稱或者代號
圖是由點和邊所組成,為了方便人了解,所以視覺化。但實際上在電腦中的儲存方式卻有很多不同的方法。可以有陣列或矩陣的方式儲存。
將圖用陣列的方式,記錄點與點之間的邊
| 0 | 0 | 1 | 3 |
|---|---|---|---|
| 1 | 3 | 3 | 4 |
把一張圖上的點依序標示編號,然後建立一個矩陣,來記錄連接資訊。方陣中的每一個元素都代表著某兩點的連接資訊。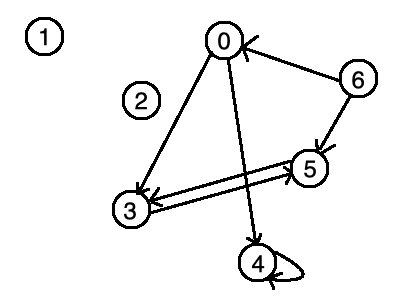
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 舉例來說,0 分別有一條連向 3 和 4 的邊,所以第 0 列的 3、4 行為 1。 |
在每一個點後方,串連所有相鄰有連接的點
無相圖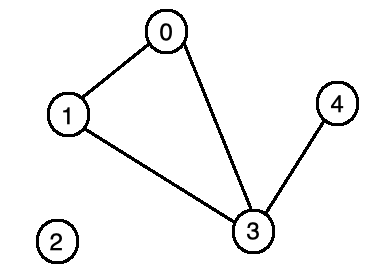
0 [1, 3]
1 [0, 3]
2
3 [0, 1, 4]
4 [3]
有向圖
0 [3, 4]
1
2
3 [5]
4 [4]
5 [3]
6 [0, 5]
(之後會另外討論~)
若兩個物件有交集關係(非空集合),就可以表示成圖。
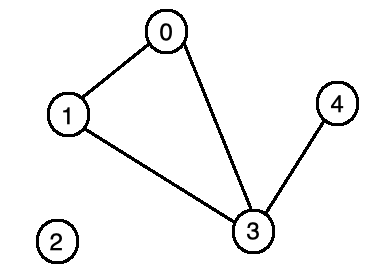
又或者是:
0 = {a, b, c}
1 = {a, d}
2 = {e}
3 = {b, d, f}
4 = {f}
是將各個物件所仰賴或依賴的對象關係表示成圖。
A > C ; E < C
B > A ; C < B
D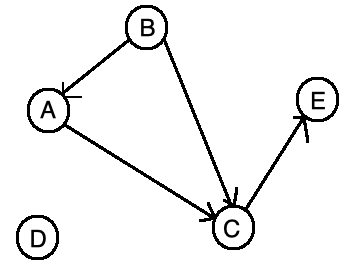
一張圖,刪除一些點、一些邊,得到的圖稱作「子圖」。原圖(沒有刪除)、空圖(完全刪除),也算是「子圖」。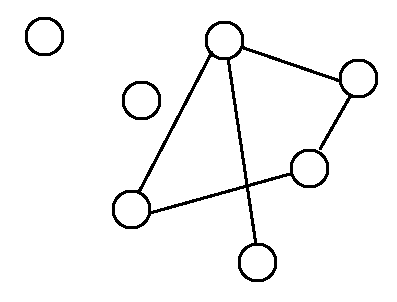
一張圖,增加一些點、一些邊,得到的圖稱作「父圖」。原圖(沒有增加)也算是「父圖」。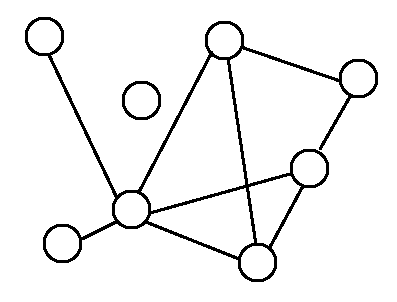
(子圖和父圖兩者是相對關係)
兩點之間,有邊變沒邊,沒邊變有邊。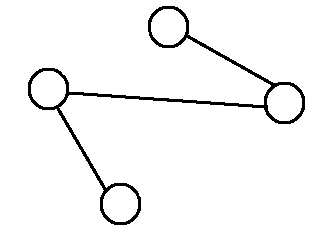
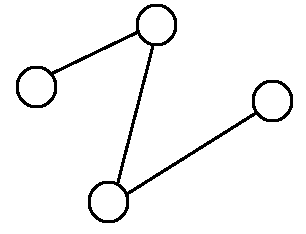
有向圖的邊顛倒過來,方向相反。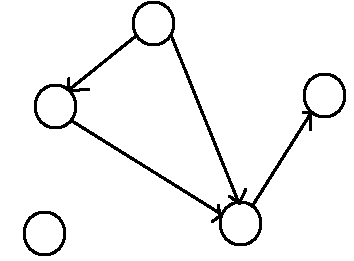
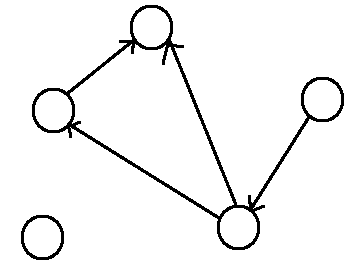
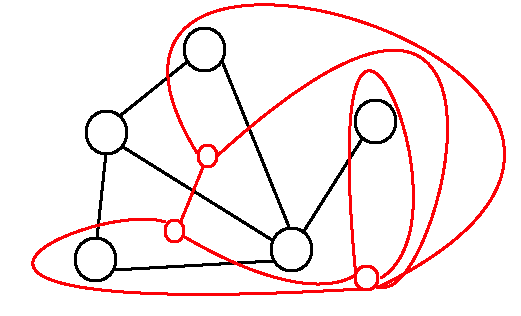
一張圖當中,觀察邊與邊關係,相鄰的邊表示成一張圖,稱作「線圖」。
(黑色為原圖,紅色為線圖)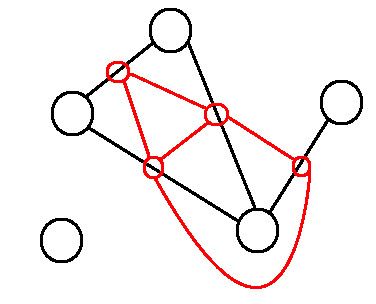
一張平面圖當中,觀察面與面關係,共邊的面表示成一張圖,稱作「對偶圖」。
(黑色為原圖,紅色為對偶圖)