昨天介紹了各式各樣的圖,今天就來討論圖的搜尋。
之前有提過深度優先搜尋,是用程式碼遞迴的概念,一層一層的我裡面找出所有可能。但之前的資料是線性的,那如果是圖的話呢?
假設我們有 1 到 5 號五個城市,八條公路,且每條公路都是單行的。我們要找出從 1 號城市到 5 號城市的最短路徑。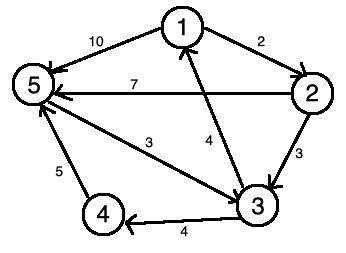
首先,要先把圖的資料轉為二維陣列 (存在矩陣 e)。
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 2 | ∞ | ∞ | 10 |
| 2 | ∞ | 0 | 3 | ∞ | 7 |
| 3 | 4 | ∞ | 0 | 4 | ∞ |
| 4 | ∞ | ∞ | ∞ | 0 | 5 |
| 5 | ∞ | ∞ | 3 | ∞ | 0 |
| 每條路的權重代表路的距離,0 代表原地,∞ 代表無法到達。 |
我們從 1 開始走,可以是:
1 → 2 → 3 → 4 → 5 路徑長度為 10
1 → 2 → 5 路徑長度為 9
1 → 5 路徑長度為 10
import numpy as np
'''
輸入驗證資料:
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3
'''
# 初始化
min1=99999999 #表正無窮
book = np.zeros(101, dtype=np.int) # 用來表示是否走過
e = np.zeros((101,101), dtype=np.int) # 用來儲存地圖資料
def dfs (cur, dis): #cur是目前所在城市編號
global min1
if dis > min1: return #如果目前走過的路已經大於之前找到的最短路徑,返回
if cur == n: #判斷是否到目標城市
if dis < min1:
min1 = dis #更新最短距離
return
for j in range(1, n+1): #從1號城市到n號城市依次嘗試
#判斷目前城市到城市j是否有路,並判斷是否再以走過的路逕中
if e[cur][j] != 99999999 and book[j]==0 :
book[j]=1 #標記城市已在路徑中
dfs(j, dis+e[cur][j]) #從城市j再出發,繼續尋找目標城市
book[j]=0 #前一部探索完畢後,取消對城市j的標記
return
#初始化二維矩陣
n, m = map(int, input().split(' '))
for i in range(1, n+1):
for j in range(1, n+1):
if i==j:
e[i][j]=0
else:
e[i][j]=99999999
#讀入城市之間的道路
for i in range(1, m+1):
a, b, c = map(int, input().split(' '))
e[a][b] = c #unidirectional
#從1號城市出發
book[1]=1 #標記1號城市已在路徑中
dfs(1, 0) #1表示目前所在城市編號,0表示已走過的路徑
print(min1) # 列印最短路徑
上面的範例是有方向性的,那如果改成無向呢?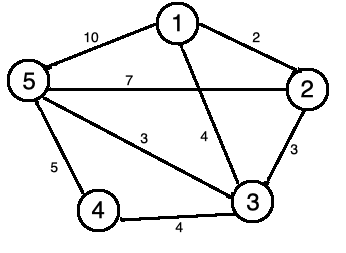
二維陣列則會改成:
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 2 | 4 | ∞ | 10 |
| 2 | 2 | 0 | 3 | ∞ | 7 |
| 3 | 4 | 3 | 0 | 4 | 3 |
| 4 | ∞ | ∞ | 4 | 0 | 5 |
| 5 | ∞ | 7 | 3 | 5 | 0 |
| 但其實程式碼只要再多加一行就可以了。 |
e[b][a] = c #bidirectional
