廣度優先搜尋 (Breadth-first Search)，也稱之為寬度優先搜尋。和深度優先搜尋不同的是，深度優先是透過函數的遞迴來延伸運算，而廣度優先則是透過「一層一層」擴展的方式來搜尋。

我們用一個圖來講解。我們要從起點走到終點，一格一格的走，但有上下左右四個方向，所以需要一層一層的擴展(用不同顏色表示)。而在程式碼的運算上，是將每個擴展的點以及步數分別加入到x、y座標和步數的佇列，最後在到達終點的時候輸出。

Start = 起點，End = 終點，Ｘ = 障礙物。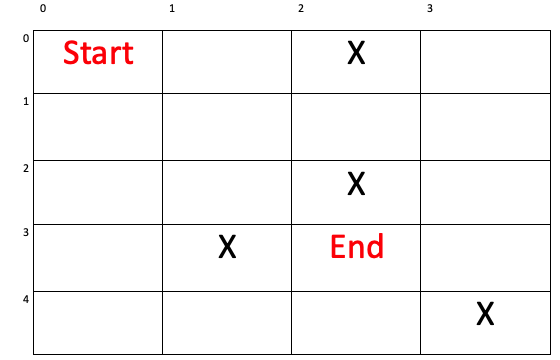

step(步數)	0
x(縱座標)	0
y(橫座標)	0
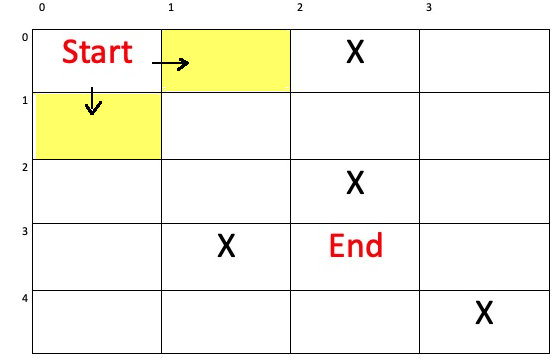step(步數)	0	1	1
-	-	-	-	-	-	-	-	-	-
x(縱座標)	0	0	1
y(橫座標)	0	1	0
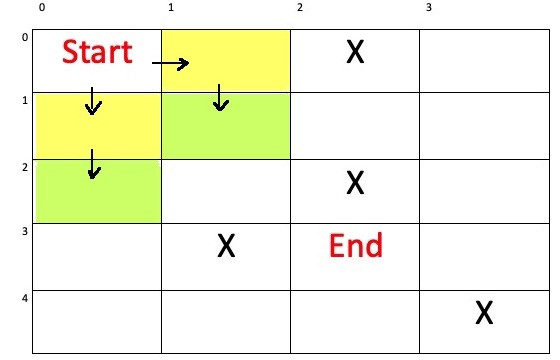step(步數)	0	1	1	2	2
-	-	-	-	-	-	-	-	-	-
x(縱座標)	0	0	1	1	2
y(橫座標)	0	1	0	1	0
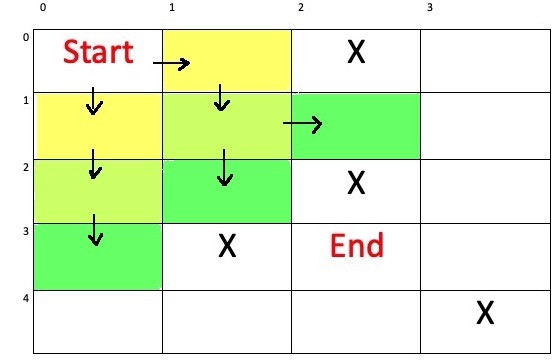step(步數)	0	1	1	2	2	3	3	3
-	-	-	-	-	-	-	-	-	-
x(縱座標)	0	0	1	1	2	1	2	3
y(橫座標)	0	1	0	1	0	2	1	0

完整的程式碼。

class note():
    def __init__(self, n, m):
        self.x = [0] * n * m  # 縱座標
        self.y = [0] * n * m  # 橫座標
        self.f = [0] * n * m  # 父親在佇列中的編號
        self.s = [0] * n * m  # 步數

# 此為迷宮，0 = 空格，1 = 障礙
maze = [[0, 0, 1, 0],
        [0, 0, 0, 0],
        [0, 0, 1, 0],
        [0, 1, 0, 0],
        [0, 0, 0, 1]]
# 設定迷宮大小
n = len(maze)
m = len(maze[0])
# 設一個陣列，用來標記走過的座標
book = []
for i in range(n):
    book.append([0] * m)

# 設定起訖點
startx = 0
starty = 0
endx = 3
endy = 2

# 定義一個表示走的方向的陣列
next = [[0, 1],   # 向右走
        [1, 0],   # 向下走
        [0, -1],  # 向左走
        [-1, 0]]  # 向上走

# 佇列初始化
head = 0
tail = 0

# 往佇列插入迷宮入口座標
que = note(n, m)
que.x[tail] = startx
que.y[tail] = starty
que.f[tail] = 0
que.s[tail] = 0
tail += 1
book[startx][startx] = 1

flag = 0 # 用來標記是否到達目標，0 = 未到，1 = 到達

# 當佇列不為空的迴圈
while(head < tail):
    # 列舉4個方向
    for i in range(4):
        # 計算下一個座標
        tx = que.x[head] + next[i][0]
        ty = que.y[head] + next[i][1]
        # 判斷是否越界
        if tx < 0 or tx > n-1 or ty < 0 or ty > m-1 :
            continue
        # 判斷是否是障礙物或者已經走過
        if maze[tx][ty] == 0 and book[tx][ty] == 0 :
            book[tx][ty] = 1  # 標記為已走過
            # 插入新的點到佇列中
            que.x[tail] = tx
            que.y[tail] = ty
            que.f[tail] = head
            que.s[tail] = que.s[head] + 1   # 步數是父親步數+1
            tail += 1
        # 若到訖點，停止擴展退出迴圈
        if tx == endx and ty == endy :
            flag = 1
            break
    if flag == 1 :
        break
    head += 1 # 當一個擴展結束後，要head++才能對後面的點再進行擴展

# 列印佇列中末尾最後一個點(訖點)的步數，但tail是指向佇列尾的下一個位置，所以要-1
print(que.s[tail-1])
print(que.x)
print(que.y)

擴展的路徑圖(佇列)。

step = 7
x = [0, 0, 1, 1, 2, 1, 2, 3, 1, 4, 2, 0, 4, 3, 4, 3, 0, 0, 0, 0]
y = [0, 1, 0, 1, 0, 2, 1, 0, 3, 0, 3, 3, 1, 3, 2, 2, 0, 0, 0, 0]