有交叉熵 Cross Entropy 的工具，我們可以對一般分類問題定義損失函數 ，理解如何評估模型優劣 ，再利用類似於線性回歸機器學習演算法 mini-batch stochastic gradient descent 就能找到參數。就不再談程式如何寫。

這些數學公式與對應演算法看似蠻高尚大的，卻無法解決肉眼一看就知道答案的下列問題：

假設有個方正國，其國民有兩個種族，橘族人主要居住在西北方與東南方；而藍族人主要居住東北方與西南方。人口普查收集了國民居住地點經緯度與種族，我們將普查的數據給畫出來如下：

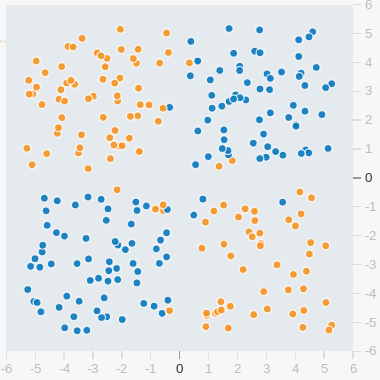
有個需求是要從居住地點（經度，緯度）這兩個特徵值來預測該國民種族分類。

很不幸的，前面洋洋灑灑的高尚大演算法是無法解這麼簡易的問題的，這個可以嘗試去 Google Introduction to Neural Networks Playgroud 去玩玩看，注意：要把『Hidden layers』減到0 為止，也就是說沒有隱藏層，可以觀察到無論如何調整超參數，讓它跑幾億個回合(Epoch)，誤差都大到無法接受。

把這個無法用一條線來區分分類的問題精簡一點，抽象成四個點分佈在四個角落，這個就變成所謂的 XOR 問題，Jayesh 在 Medium 有一篇論述 談論到演算法發展，如同該文的衍述，隨後我們馬上要進入 深度學習的 Hello World - 多層感知機 MLP，方能解決普遍性，包含非線性，的問題。

『多層感知機』 MLP 推理邏輯

我們一樣由 Mxnet Guon的中/英教學來推論這個技術。

我們先很直觀的在上一篇文章中的一般性分類問題，他長成這樣子：

可以用
來表達

有人說是模擬腦神經，或者受該學科的啟發，在中間多加一層隱藏層（五個單元），該層的每個單元與輸入層（四個單元，想成四個特徵值）每個單元都連接一起，同時他又與輸出層（三個單元，亦即三種類別）每個單元都連接一起：

那這個網路我們可以如此表示：
#隱藏層是由輸入層與(隱藏層參數)計算取得
#輸出層是由隱藏層與(輸出層參數)計算取得

其實我們可以任意加多個隱藏層，就是這樣一層一層疊上去。不過為了保護眼睛，我們就只加一層隱藏層即可做點證明。這樣三層的結構，我們繼續推導數學：

=

看到最後居然變成是 ， 也就是。是不是覺得與之前『沒有隱藏層』淺層網路，沒有什麼差異？因為 還會是另一個 W；也會是另一個 b。如果有這種感覺，你大約是懂所謂的 Affine Transformation。線性代數是有談到對矩陣疊加好幾次Affine Transformation，仍然是 Affine Transformation。亦即我們就算再多加幾層隱藏層到模型，他還是維持原來一樣，沒有隱藏層的。

有個辦法，那就是再導入非線性的函數在裡面，亦即在隱藏層的每個單元都套上一個非線性函數，並且為這個取個名字『激活函數』Activate Function，當然這也要說成是被神經突觸啟發的靈感，這樣人工神經網路就成顯學。

問題來了每個單元都套上一個非線性函數，那有無窮的選項。古代（也許就只有兩年前，這學科進步太快，以月份在進化的）常用Sigmoid function (亦即 ) 。但是近日實務上發現用 ReLU (Rectified LinearUnit) 對訓練來講，也相當優異，而且計算更容易了：

不用多說，反正就是小於0的就是把他變成0，其他維持原來值。畫個圖看看：

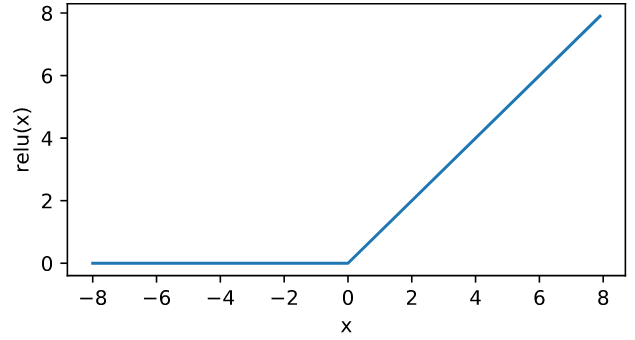
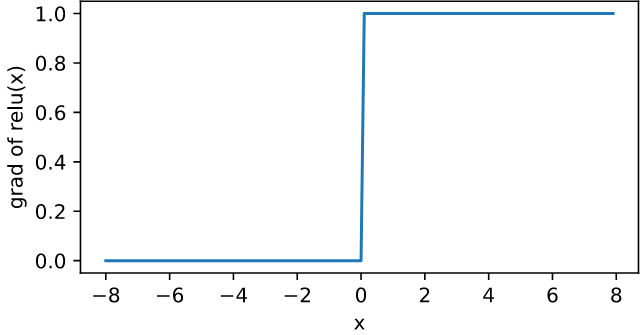
因為要計算梯度，從圖形來看 x 為負值時，ReLU(x)的導數是0 (因為是平躺)：大於0時，它的導數是1 (斜率是1的斜線)：但是當 x=0 時，明顯就是不可微，我們只好幫它設個值0。所以 ReLU(x) 的導數圖形如下：

多層感知機 MLP

有了激活函數，我們就可以真正堆疊一層隱藏層：

# (代表激活函數，我們打算用 ReLU。當然也可以用其他的如 Sigmoid 函數)

當然一樣還要加 softmax 函數，才能做分類問題，請參考下面更多層的感知機。

如果要更複雜的模型，我們也可以堆疊好幾層隱藏層, 例如下面圖示兩層的隱藏層：

這時候我們就這樣表達有 n 層隱藏層的網路：


……

不過我們可是要做分類問題，所以最後輸出要靠上一篇文所講的 softmax 做整個模型的最後輸出。

後面又跟一般分類問題甚至二元分類問題一樣，要定義損失函數例如用我們前幾篇文講到的『交叉熵損失函數』，然後可以用 mini-Batch 隨機梯度下降來訓練網路。明天我們做做看。

最後再提一下，多層感知機 MLP 也是可以做迴歸問題，例如：預測年收入多少。這個只要把模型改為輸出只有一個單元，同時也不需要 softmax 了。而它要用的損失函數可改用之前講過得MSE函數，一樣的我們可以用 mini-Batch 隨機梯度下降來訓練。

後記：

在 Fields 一口氣把機器學習這些最基礎的數理理論講完，佳麗感慨："原來人工神經網路對我來講是一場夢，我還以為真的可以看到仿照神經細胞與突觸所製作出來的計算處理器呢！結果全部是數學公式。"

Molly 告訴大家，他其實是有看到『仿神經型態系統』Neuromorphic System 以生物神經系統的構成、訊號傳遞與運算記憶功能進行電子電路材料、元件、電路模擬、電路設計、運算架構、演算法、系統等的工程仿真 1-3，包括突觸（synapse）、神經元（neuron）、脈衝神經網路（spiking neural network）、視覺系統、聽覺系統、嗅覺系統等（取自泛科技）。但是此領域的發展至今還沒形成可以商業應用，也許可以考慮當作T軟的AI方向之一。

備註：

專案緣起記錄在 【UP, Scrum 與 AI專案】