有了Day3基本的數學工具後,接著來看看怎麼去求解數學模型。整個最佳化求解可以分為,無限制條件及有限制條件,今天就先從無限制條件的最佳化求解開始。
根據函數變數的數量可將函數分為單變數函數與多變數函數,這兩種函數各有一些求解條件。
若為
之局部最小點,則
由泰勒級數展開式來觀察,已知為駐點(斜率為0的點)則,
or
,取決於
or
若 且
,則
為
之局部最小值。
若 且
,則
為
之局部最大值。
若 為
之局部最小值,則
若 為
之局部最大值,則

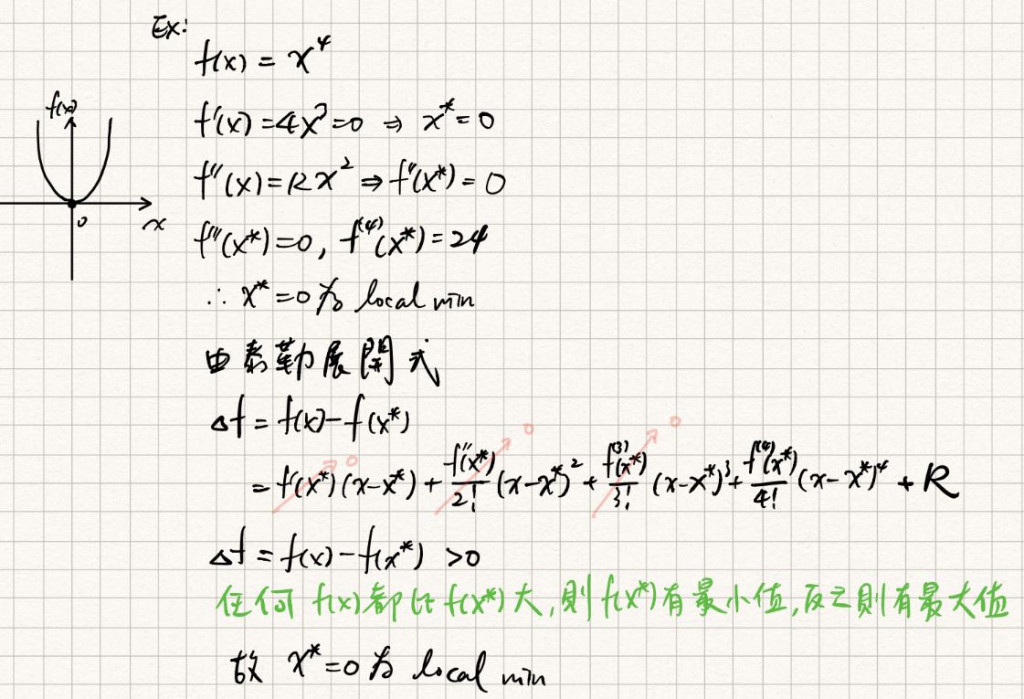
若為
的局部最小點 ,則
or
若 且
為正定,則
為
的局部最小點。
若 且
為負定,則
為
的局部最大點。
多變數函數在
之泰勒展開式,
其中
則的大小(>0, 0<, 或=0),取決於二次式之正、負或者
之形式。
若為
的局部最小點,則
為正定或半正定。
[提醒]當遇到非線性方程式時,駐點未必可用解析方式求得