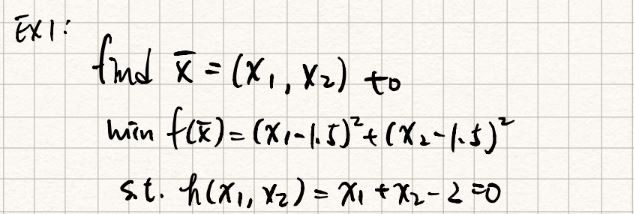今天來討論具有複雜結構的最佳化問題。在實際的問題中，勢必存在著對獨立變項的限制條件，比如說如何在有限的成本中，獲取最大利益，此時就須要考慮較複雜的模型。

限制條件可分為等式限制以及不等式限制(此處都以多變量函數為主)，等式限制會談到Lagrange Multiplier Theorem，不等式限制則會提到Karnh-Kuhn-Tucker Theorem。

先來介紹限制條件的最佳化之一般化模型，
find a design vector to
min
s.t.

限制條件會影響最佳解出現的位置。如下圖，限制條件就是藍色線，解就只能從X軸、Y軸以及藍色線所圍起來的空間中去選取，此空間稱為feasible region。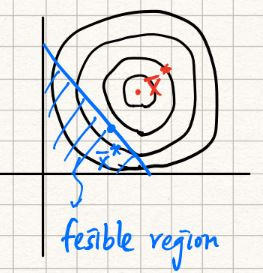

等式限制之必要條件

Find to
min
s.t.

正則點(Regular point)，

定義

若，且在點可使限制條件函數之梯度向量為線性獨立，則點稱為正則點。

Lagrange Multiplier Theorem
令為一正則點，且為上述問題之區域最小點，則存在一組Lagrange multiplier ，使得

定義

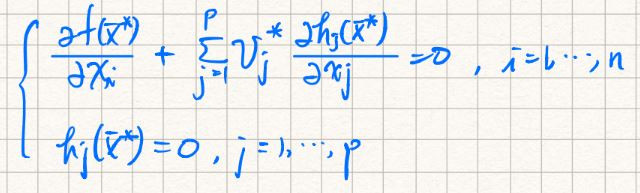
Lagrange function

範例