上次我們提到了針對有限制條件之最佳化中的等式限制條件，可以利用Lagrange multiplier theorem來求解。今天更一進步討論不等式限制條件該如何計算。

不等式限制條件的型式為，

一旦遇到不等式限制條件，第一步就是轉成等式限制條件，

其中為鬆弛變數(slack variable)
當 or ，此時為Active constraint
當 or ，此時為Inactive constraint

Karnh-Kuhn-Tucker必要條件

KKT定理

令為可行區域內之一正則點，且為滿足與的局部最小點，若定義該最佳化問題之Lagrange function如下:

Note:(4)式稱為switching conditions。一般而言，有m個不等式限制條件，則可產生個不同的正常解組合。
例如:
當，則(4)式為，故有種答案組合
即

本題，有種答案組合

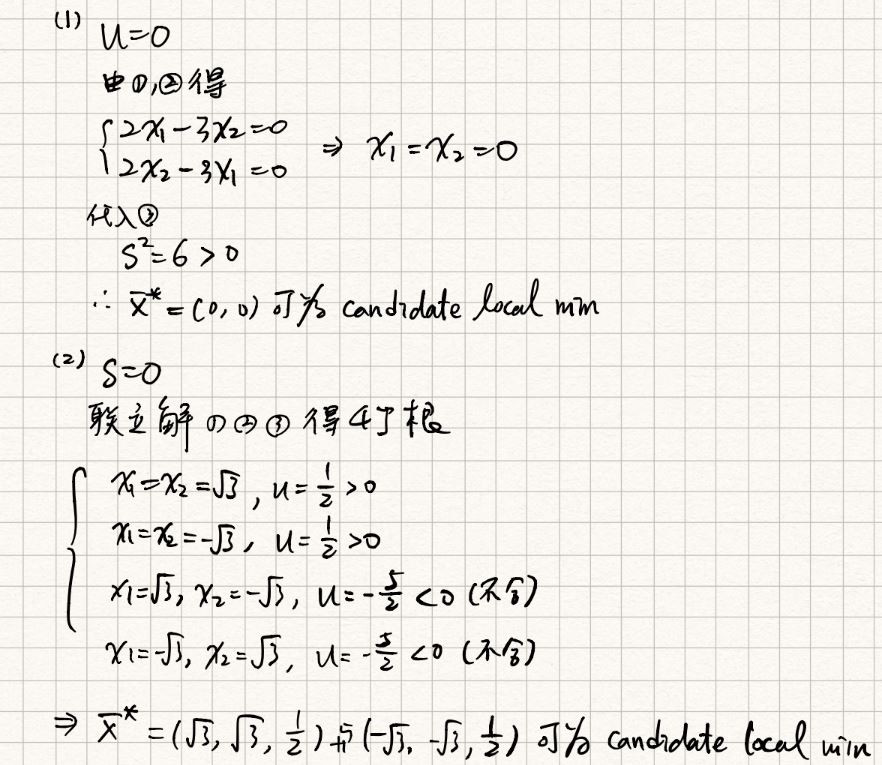
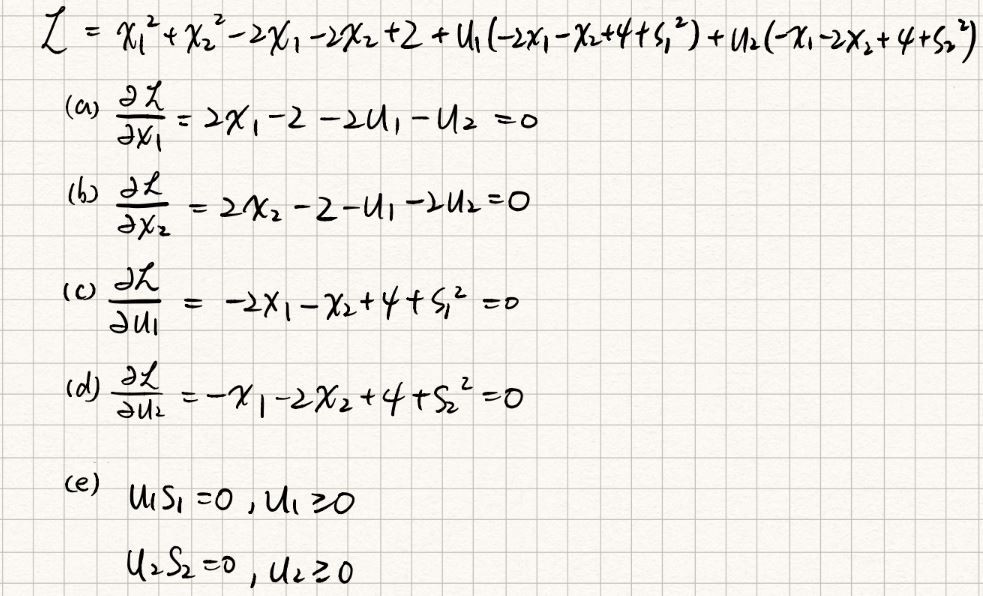
Note:

1. 不等式限制條件在active constraint的情況下要去檢驗是否為正則點，但是只有一個限制條件時無需檢驗，因為它必為正則點。
2. 檢驗方法為，確認彼此是否為線性獨立。