Art and Science of Machine Learning

A pinch of science

Regularization for Sparsity

再稍微提及一下關於L1與L2的問題，針對大型的model與稀疏的輸入，有幾個議題必須去被解決

我們實際利用tensorflow playground來實做看看我們使用所有的特徵並且加上一堆的神經元
觀察比較看看加入L1 Regularization與沒有加入的成果有何不同

• 未加入的可以看到雖然可以將數據做分類，但看到輸入層與隱藏層的神經元連結必須一直更新權重，這樣非常的耗能並且模型會很大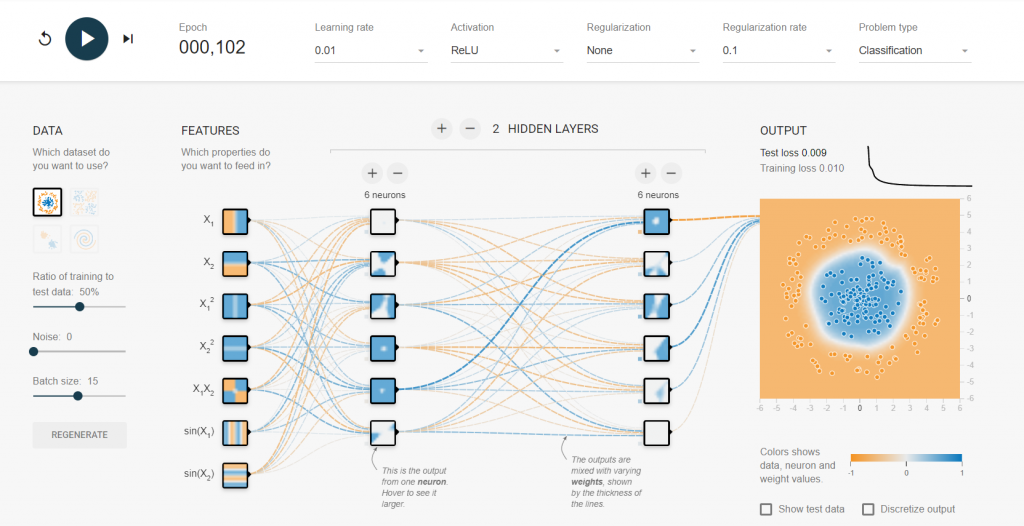
  

• 看到加入L1 Regularization除了能夠分類數據外，更能夠更平滑的處理所有數值，在權重的選擇上只有兩個參數會被當作輸入，大大解決我們上述所講的問題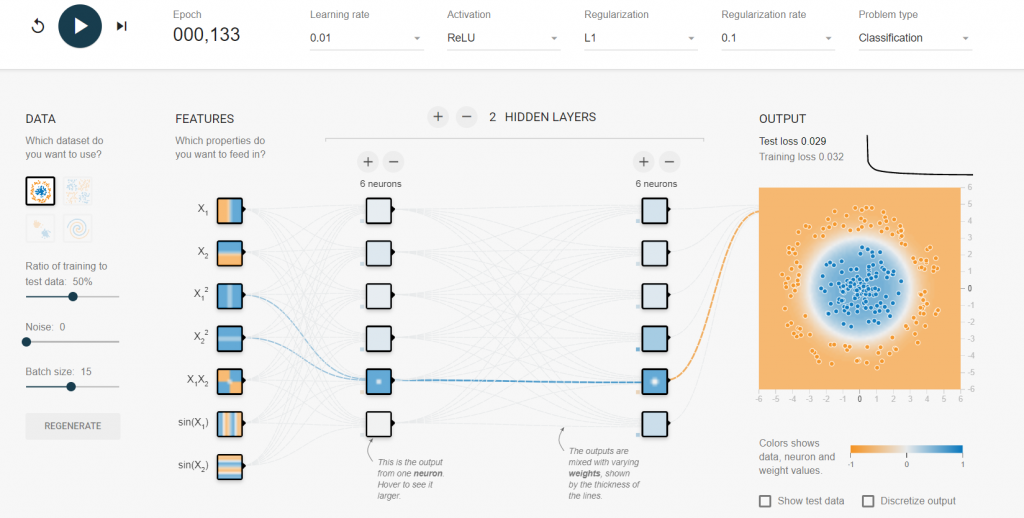
  

Logistic Regression

Logistic Regression中文叫做邏輯回歸，那跟線性回歸有甚麼不一樣呢??
線性回歸像是使用一條直線去擬合所有數據點，而邏輯回歸的概念是利用一條線把所有數據分開
最常使用的就是sigmoid的激活函數，由下圖可以看到其公式以及函數圖形
這個圖形會被當作分類模型的函數，最主要的原因就是他是依照輸出機率與原本線性模型做加總進行結合
所以能夠直接利用線性回歸的概念來做轉換
通常來說都會使用cross-entropy作為評斷標準，在我之前的文章中有說過其公式有興趣的人可以去看看

sigmoid 缺點

但這激活函數也不是完全沒有壞處，我們可以看到下面這張圖
大家特別注意一下右上角跟左下角，若推廣到無限大的範圍裡，會接近一條水平線，那大家應該都知道水平線微分永遠等於0吧
這不就代表經過此函數就會一直不動，那就等於我要很久才會完成此次訓練了嗎

early stopping

除了我們上述講到的問題以外，其實還有一些方法針對overfitting來做防範
如果有自己訓練過模型的一定知道，如果放著模型然後就去做其他事、沒在注意其變化的下場就是訓練、測試的loss慢慢的分開
這當然是我們不願看到的情況，但我們也不可能時時刻刻都盯著電腦螢幕看它們的狀況
所以early stopping就是一個非常好用的方法，其實它的概念很簡單就是只要validation逐漸上升就把它停止，儲存最好的模型參數就這麼簡單

ROC curve and AUC

最後介紹一下ROC跟AUC曲線，在開始前要先複習一下混淆矩陣的概念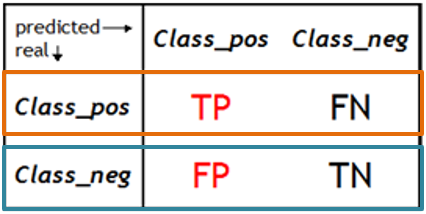

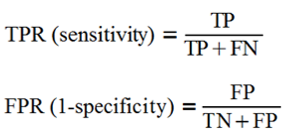
TPR為真實數據正向中預測為正向的機率、FPR為真實數據反向中預測為正向的機率
所以我們希望TPR越高FPR越低是我們所期待的，我們可以依照上述方法畫出一條曲線，接著依照我們的要求其設定threshold，可視化的觀察其結果並檢驗曲線是否合理與優良

而AUC(Area-Under-Curve)淺而易見的概念就是曲線下的面積，，根據附蓋的面積越大代表分類效果越好，最常判斷的方法就是畫一條從原點出發的斜直線，接著若是AUC面積大於此斜線所涵蓋面積那代表此分類器基本上有50%的機率能夠預測成功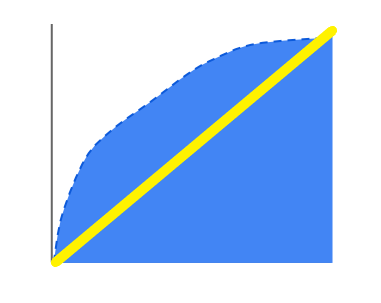

※圖片參考至 Art and Science of Machine Learning slide