前言

這幾天的文章會是一系列的，會需要一起看才比較能看懂整個ML模型的輪廓，
然而因為一天能寫的內容量有限，所以我會在前言部分稍微說明我寫到哪。

複習一下ML的整個訓練過程

因為ML模型的訓練階段章節內容會分很多部分，我們要先確認好自己在哪個階段，
以免吸收新內容卻不知道用在內容的什麼地方。

★ML的整個「訓練過程」：這裡以監督式學習(Supervised Learning)為例

而今天的文章我們要來討論一下「加快ML模型訓練的方法」。

Course - Launching into Machine Learning

第三章節的課程地圖：(紅字標記為本篇文章中會介紹到的章節)

• Optimization
  • Introduction to Optimization
    • Introduction
  • Defining ML Models
    • Defining ML Models
    • Introducing the Natality Dataset
  • Introducing Loss Functions
  • Gradient Descent
    • Gradient Descent
    • Troubleshooting a Loss Curve
    • ML Model Pitfalls
  • TensorFlow Playground
    • Lab: Introducing the TensorFlow Playground
    • Lab: TensorFlow Playground - Advanced
    • Lab: Practicing with Neural Networks
    • Loss Curve Troubleshooting
  • Performance Metrics
    • Performance Metrics
    • Confusion Matrix
  • Module Quiz

0. 一樣先來個重點整理，下面會有詳細介紹

• 加速訓練的方法：
  • 調整「計算偏微分時的資料總數」
    • 利用batch的方法
  • 調整我們「檢查loss的頻率」
    • 基於固定時間(Time-based)的檢查
    • 基於固定步驟(Step-based)的檢查
• 一大堆有關batch的名詞整理：

• batch size與迭代(iteration)與epoch的概念比較：

假設我現在有400筆資料，我做分堆：
我決定一堆的大小(batch size)要有40筆資料，
這樣一共會有10堆(通常稱為number of batches,batch number)，
也就是說每一輪我要學10堆資料，也就是學10個迭代(iteration)。
學完「10個迭代(iteration)」後，等於我把資料集全部都看過一次了。
這樣就是一輪(epoch)訓練的結束。
.
會有batch size與迭代(iteration)與epoch這些詞的原因，
是因為通常ML學習的資料量都很大，我們會需要分比較小堆。

1. ML Model Pitfalls

課程地圖

• Optimization
  • Gradient Descent
    • ML Model Pitfalls

有個常見的情況是，每次當我們重新訓練ML模型的時候，
明明是一樣的code，我們也希望能產生一樣的實驗結果，但往往結果不同。
但通常我們會希望每次訓練的結果皆相同，這樣才是一個穩定的模型。

在ML裡面，很多時候我們再進行第二次訓練時，即使使用完全相同的hyperparameter
最後訓練出來的參數(parameter)結果也會完全不同。
這似乎是不太好的現象，我們希望尋找的是一個最佳參數(parameter)解，
結果不同，難道是gradient descent無效或是我們實作錯誤嗎?

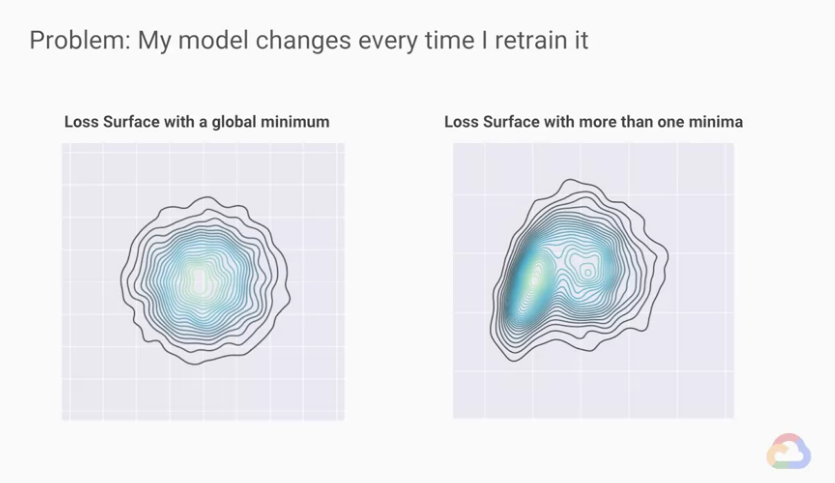
並不一定，我們從上圖可以看出，當我們在搜尋Loss的表面時，
Loss的表面可能不單純像左圖只有一個山谷，
像右邊多於一個山谷的才是比較常見的Loss表面，
這個特性有個名稱叫做凸性(convexity)

• 左邊的是convex surface(凸面)
• 右邊的是non-convex surface(非凸面)

為什麼loss surface可能會有不只一個最小值?

這意思是在參數空間(parameter space)中有很多等值(或接近等值)的點，
(這裡的等值 = 參數算出來的loss等值)
也就是說這些參數的設置，都能是「具有相同的預測能力」的ML模型。

自己的註：

也就是說，不同的參數組合，算出「一樣的loss」，等於具有「相同的預測能力」。

我們會在稍後介紹神經網路(neural networks)再更仔細的討論這問題。
(因為這樣的情況主要發生在神經網路(neural networks))

我們只要先記得loss surface會因為擁有的最小值數量，而有不同數量的山谷。

自己的註：

最大值(最小值)有分成兩種：local maxima(minima), global maxima(minima)
local指的是區域性的，也就是一個範圍內的最大(最小)
global指的是全域性的，也就是全部範圍內的最大(最小)
以山來比喻，山都會有主峰，主峰就是全部(global)最高的山，
但除了主峰之外還有有次高峰、第三高峰...，這些都是區域性(local)的最高。
我們指的很多山谷就是因為有很多local minima，然而最深的谷只會有一個。

我們在訓練時，時常會覺得完成訓練時間太長，我們要來思考怎麼樣可以加快我們的訓練速度?

不過為了要討論這問題，我們先從比較高階的角度看所有的步驟，
並從演算法的角度去分析他們的time complexity，

我們將訓練的主要演算法分成三大步驟：

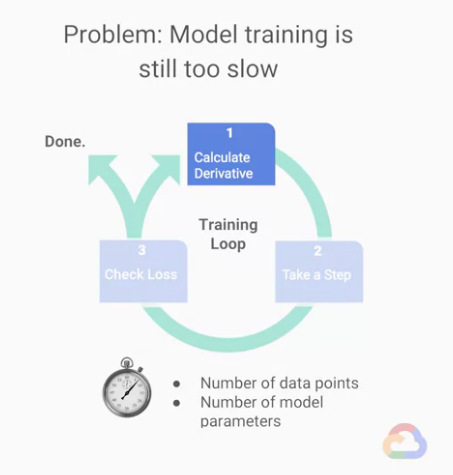
★Step 1 : 計算導數(偏微分)，上圖

• 當我們計算偏微分時，「計算的時間成本」會與我們需要放入loss function的「比較資料數量」成正比，也會與我們ML「模型參數的總量」成正比。
  • 而「模型參數的總量」可以從數千到數億個不等。
  • 同樣的「比較資料的數量」也可以從數千到到數千億不等。

自己的小註記：

Step 1 : 計算導數(偏微分) 這階段影響訓練速度的關鍵在於：

• 模型參數(parameters)的總量
• 比較資料(label)的數量

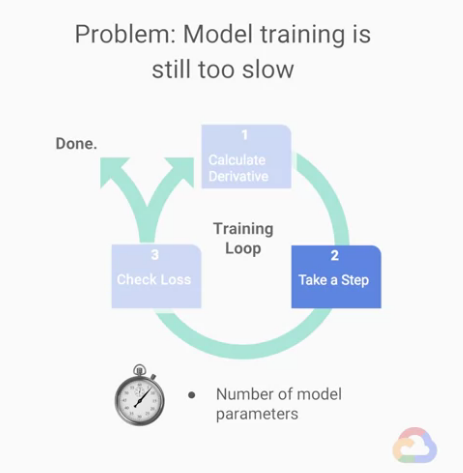
★Step 2 : 參數更新

在這張圖中，「每個循環」也代表會「參數會更新一次」，
而這「時間成本」僅由模型內「參數的數量」影響，
然後，相對其他步驟，「更新參數」時間的時間成本較小。

自己的小註記：

Step 2 : 參數更新 這階段影響訓練速度的關鍵在於：

• 模型參數(parameters)的總量
  -> 但「更新參數」本身影響的時間相對其他步驟不多。

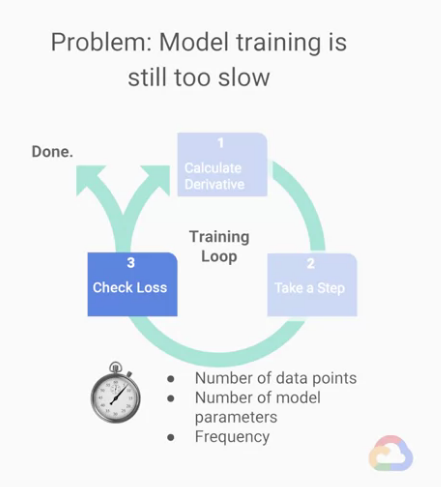
★Step 3 : 檢查loss

我們來想一下計算Loss的時間，這個步驟的時間複雜度，
會與我們的「想要計算loss的總資料數(label數)」與「我們模型的複雜度」成正比，

但特別的是，即使我們說這一個循環有這三個步驟，
但「檢查loss」的步驟不需要每次都做，
因為通常loss function的變化都是在逐漸好的方向變化。

自己的小註記：

Step 3 : 檢查loss 這階段影響訓練速度的關鍵在於：

• 想要計算loss的總資料數(label數)
• 模型參數(parameters)的總量
• 檢查 loss 的頻率

所以經由上述簡單的討論，我們應該心理先有個底了，
我們該怎麼做才能加快訓練的速度呢?

• 首先，模型裡面的參數如果是固定的數量，
  未來我們會提到我們可以將裡面的參數做「正規化(regularization)」
• 另外，雖然減少檢查loss的總資料數(label數)聽起來會有用，但我們通常不建議這樣做。

自己的註：

正規化(regularization)：可以讓模型的數字被限制在一定的範圍，
例如原本所有的ML模型內的參數可能介於「1~1000」，
透過正規化(regularization)的縮放，我們可以縮小1000倍(只是舉例)，
參數就會變成「0.001~1」，這樣的好處在於我們可以避免做「大數運算」。

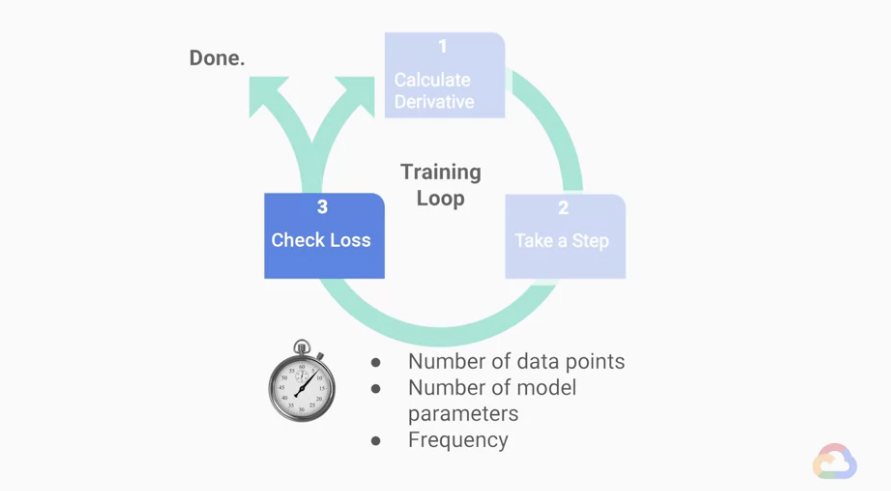
取而代之的，我們有兩大手段作為我們加快訓練速度的關鍵：

• 調整我們「計算偏微分時的資料總數」
• 調整我們「檢查loss的頻率」

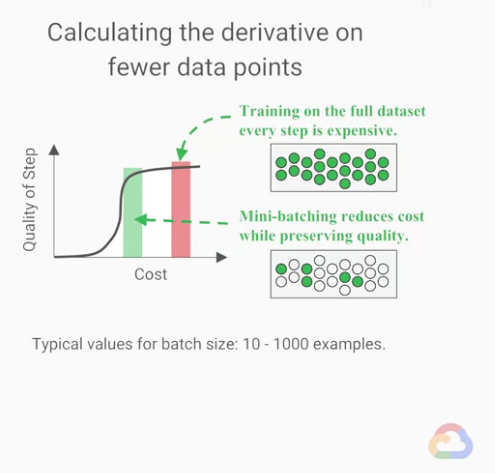
正如同我們前面所說，我們能加快模型訓練速度的關鍵之一是「調整我們計算偏微分的資料數」

記得：

偏微分來自於我們的loss function，
而我們的loss function是將很多預測的error組合在一起的值。

所以這個方法需要減少「我們給loss function」的資料總數在每一輪迭代(iteration)中，
到這裡，我們可以先停下來想一下為什麼這樣是可以的。

為何這個方法沒有問題?

主要是因為我們可以從我們的訓練資料中抽取樣本，
而這個樣本與其他相比是平均且平衡的。
我們在之後會講到關於抽樣的陷阱以及如何避免，
而現在我們先知道抽樣的策略是從我們的資料集用統一的機率抽樣的。
所以所有在訓練資料集的例子都有一樣均等的機會被模型看過。

在ML中，我們將這種在從訓練集中抽樣的做法稱為mini-batching，
原本我們所計算的gradient descent預設會使用所有的資料集，
然後使用mini-batching的資料，我們可以算出mini-batch gradient descent，
而這些資料被抽樣出的資料被稱為batches。

mini-batch gradient descent具有許多的好處：

• 花費更少的時間運算
• 使用更少的記憶體
• 很容易做平行運算

另外一個很常聽到的名稱term batch gradient descent，
batch指的是以分批(batch)的方式來處理，
所以batch gradient descent會計算整個資料集，
與mini-batch gradient descent不相同。

這裡我們討論的是mini-batch gradient descent，
但有個常讓人搞錯的地方是，mini-batch size時常被稱作batch size，
TensorFlow也是這樣稱呼的，所以我們也這樣稱呼他。

在之後的討論中，如果我們討論到有關於batch size的事情時，
我們就是在討論mini-batch gradient descent的「樣本數大小」。

自己的註：

這邊名詞太多覺得很混亂嗎XD?
簡單整理一下：

★另外再送大家batch size與迭代(iteration)與epoch的概念比較：

假設我現在有400筆資料，我做分堆：
我決定一堆的大小(batch size)要有40筆資料，
這樣一共會有10堆(通常稱為batch number,number of batches)，
也就是說每一輪我要學10堆資料，也就是學10個迭代(iteration)。
學完「10個迭代(iteration)」後，等於我把資料集全部都看過一次了。
這樣就是一輪(epoch)訓練的結束。
.
會有batch size與迭代(iteration)與epoch這些詞的原因，
是因為通常ML學習的資料量都很大，我們會需要分比較小堆。
.
參考資料：神經網路中Epoch、Iteration、Batchsize相關理解和說明

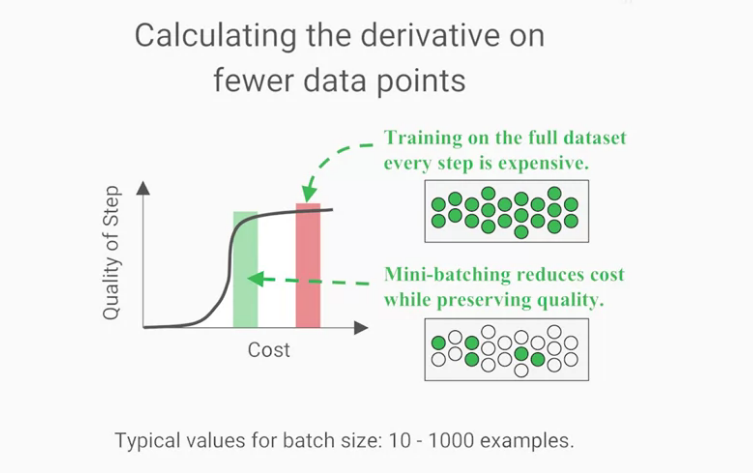
我們來討論一下那mini-batches應該有多大?
batch size也像learning rate一樣是hyperparameter，
而且同樣的，這兩個的最佳值都是「因題目而異」的，
我們一樣可以使用hyperparameter tuning的方法找到他，
我們也會在後面一並詳細介紹。

通常batch sizes會介於10~1000個樣本之間。

另外一個我們提到加速訓練的關鍵是改變我們檢查loss的頻率，
稍微想一下，儘管一個個檢查每一個資料集的子集合是好事，但未必對訓練時間是好的。

上面是我們將我們的講法轉換後寫出的code，想法非常的簡單，
我們加入一些邏輯，使得計算loss function的高時間代價能夠減少計算的頻率，

現代檢查loss function的頻率很多有名的策略：

• 基於固定時間的檢查(Time-based) -> 例如：每三十分鐘檢查一次loss
• 基於固定步驟的檢查(Step-based) -> 例如：每一千個步驟檢查一次loss

我們減少檢查loss的頻率，並且引入mini-batching這套方法，
我們開始將模型訓練的兩個基本部分分開並各自調整，
「更改我們模型的參數」與「檢查我們是否有做正確的修正」。

參考資料

• coursera - Launching into Machine Learning 課程
• 神經網路中Epoch、Iteration、Batchsize相關理解和說明
• 若圖片有版權問題請告知我，我會將圖撤掉