動力系統建模簡單來說可以分成兩個部分,1)將問題以微分方程來表示,2)求解微分方程。第一部份需要對問題有一定程度的背景知識,例如模擬自駕車的行走,需要對運動學有一定的了解,當有了數學表達式,剩下的就是求解了。然而,並非所有的問題都可以求出解,所以衍生了很多理論與技巧,來達到這個目的。因此,我們今天介紹一個最簡單能夠達到所需精確度的求解微分方程的方法,尤拉方法。
考慮一個連續時間的動力系統
其中且
,初始條件為
。
從初始條件開始,利用慢慢逼近方程式的解
變量:步後的時間
在時刻
的第1個狀態變量
在時刻
的第2個狀態變量
步數
模擬停止的時間
輸入:
Pseudo code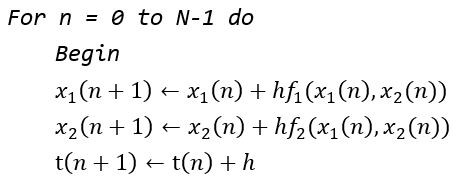
輸出:
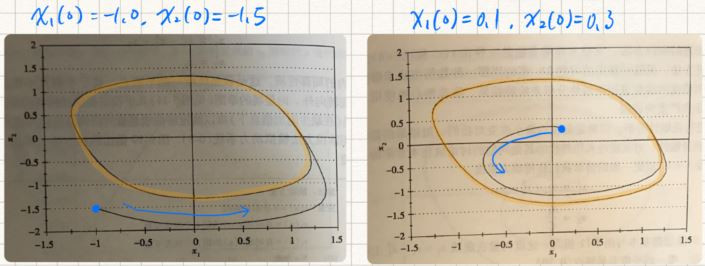
有一微分方程組
給定兩組初始值,觀察解的行為(如下二圖),可以發現解都逼近同一條繞著原點的封閉軌跡,此軌跡被稱為極限環。