Day 24 : 機率模型簡介

第 11 屆 iThome 鐵人賽

DAY 24

AI & Data

連接數學與現實世界的橋樑 -- 數學建模系列第 24 篇

11th鐵人賽

spidyjames

2019-09-25 23:59:45

901 瀏覽

分享至

從今天起我們將邁向數學建模的第三部分，機率模型。許多現實生活問題都包含著不確定因素，因此便引入了隨機變量來描述這些不確定性，利用機率論的方法可使得數學建模更加實用。

統計學簡介

假設 $X$ 是獨立的隨機變量，若 $X$ 為離散的情況，則期望值或平均值為 $E(X) = \sum x_k Pr \left{X = x_k \right}$
若 $X$ 為連續，帶有密度 $f(x)$ ，則期望值為 $E(X) = \int xf(x) dx$
變異數的定義為，變數與平均數差異的程度，
$V(X) = E(X - E(X))^2$
若 $X$ 為離散，則為 $V(X) = \sum (x_k - E(X))^2 Pr\left{X= x_k \right}$
若 $X$ 為連續，則為 $V(X) = \int (x_k - E(X))^2 f(x)dx$
中央極限定理，當 $n \rightarrow \infty$ 時， $X_1 + \dots + X_n$ 的分配會趨近於常態分配。尤其是如果 $\mu = E(X)$ , $\sigma^2 = V(X)$ ，則對所有實數 $t$ ，
$https://chart.googleapis.com/chart?cht=tx&chl=lim_%7Bn%20%5Crightarrow%20%5Cinfty%7D%20Pr%20%5Cleft%7B%20%5Cfrac%7BX_1%20%2B%20%5Cdots%20%2B%20X_n%20-%20n%5Cmu%7D%7B%5Csigma%20%5Csqrt%7Bn%7D%7D%20%5Cle%20t%20%20%5Cright%7D%20%5Crightarrow%20%5CPhi%20(t)$
其中 $\Phi (t)$ 為標準常態分配，其密度函數對所有 $x$ ， $https://chart.googleapis.com/chart?cht=tx&chl=g(x)%20%3D%20%5Cfrac%7B1%7D%7B%5Csqrt%7B2%20%5Cpi%7D%7D%20e%5E%7B-%20%5Cfrac%7Bx%5E2%7D%7B2%7D%7D$ ；對所有的 $t$ 有 $https://chart.googleapis.com/chart?cht=tx&chl=%5CPhi%20(t)%20%3D%20%5Cint_%7B-%20%5Cinfty%7D%5Et%20%5Cfrac%7B1%7D%7B%5Csqrt%20%7B2%5Cpi%7D%7D%20e%5E%7B%5Cfrac%7B-x_2%7D%7B2%7D%7D$
標準常態分配圖形如下，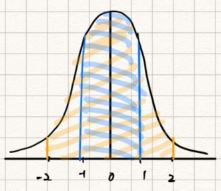

曲線下面積約為1，橘色區域約為0.95，藍色為0.68。
橘色區域範圍可表示為 $https://chart.googleapis.com/chart?cht=tx&chl=-1%20%5Cle%20%5Cfrac%7BX_1%20%2B%20%5Cdots%20%2B%20X_n%20-%20n%5Cmu%7D%7B%5Csigma%20%5Csqrt%7Bn%7D%7D%20%5Cle%201$
橘色區域範圍為 $https://chart.googleapis.com/chart?cht=tx&chl=-2%20%5Cle%20%5Cfrac%7BX_1%20%2B%20%5Cdots%20%2B%20X_n%20-%20n%5Cmu%7D%7B%5Csigma%20%5Csqrt%7Bn%7D%7D%20%5Cle%202$
因此我們可以說有68%的把握 $X_1 + \dots + X_n$ 會落在 $n\mu - \sigma \sqrt{n} \le X_1 + \dots + X_n \le n\mu + \sigma \sqrt{n}$ 內;
有95%會落在 $n\mu - 2\sigma \sqrt{n} \le X_1 + \dots + X_n \le n\mu + 2\sigma \sqrt{n}$ ，這就是區間估計的概念。

範例

過去一年內，一個社區的消防中心平均每月會接到171通火災電話，基於這資料房屋的火災警報率被估計為171月/次，當下個月收到通報只有153次，則可以說火災率減少了還是只是一個隨機波動。

提出問題
變量:
$\lambda =$ 通報的房屋火災率(每月)
$X_n =$ 第 $n-1$ 次與第 $n$ 次火災之間的時間(月)
假設:
房屋火災以速率 $\lambda$ 隨機發生，亦即 $X_1, X_2, \dots$ 是獨立且每個 $X_n$ 為參數 $\lambda$ 的指數分配
目的:
給定 $\lambda = 171$ ，確定153次火災警報的機率有多大
確定建模方法
根據問題的特性，使用區間估計進行處理
推導模型的數學表達式
假設火災警報間的時間 $X_n$ 服從指數分配
$f(x) = \lambda e^{-\lambda x}$
$https://chart.googleapis.com/chart?cht=tx&chl=%5Cmu%20%3D%20%5Cfrac%7B1%7D%7B%5Clambda%7D$
$https://chart.googleapis.com/chart?cht=tx&chl=%5Csigma%5E2%20%3D%20%5Cfrac%7B1%7D%7B%5Clambda%5E2%7D$
求解模型
給定95%的信賴區間，將已條件帶入，可得 $https://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7B153%7D%7B171%7D%20-%20%5Cfrac%7B2%20%5Csqrt%7B153%7D%7D%7B171%7D%20%5Cle%20X_1%20%2B%20%5Cdots%20%2B%20X_n%20%5Cle%20%5Cfrac%7B153%7D%7B171%7D%20%2B%20%5Cfrac%7B2%20%5Csqrt%7B153%7D%7D%7B171%7D$
$\Rightarrow 0.75 \le X_1 + \dots + X_n \le 1.04$
表達分析結果
斷言火警降低是不充分的，接到的電話數變少比較是隨機波動。