什麼是非監督式學習
之前我們所介紹的幾種分類方法都監督式學習，而非監督式學習演算法只基於 輸入資料找出模式，無法正確找出結果。K-Means就是透過這個概念將資料做分群，顧名思義就是將資料分成一群一群。常被用在客戶分群、特徵抽象化、非結構化資料分析…。

下面這張圖可以明顯看出左邊是監督式學習，右邊是非監督式學習。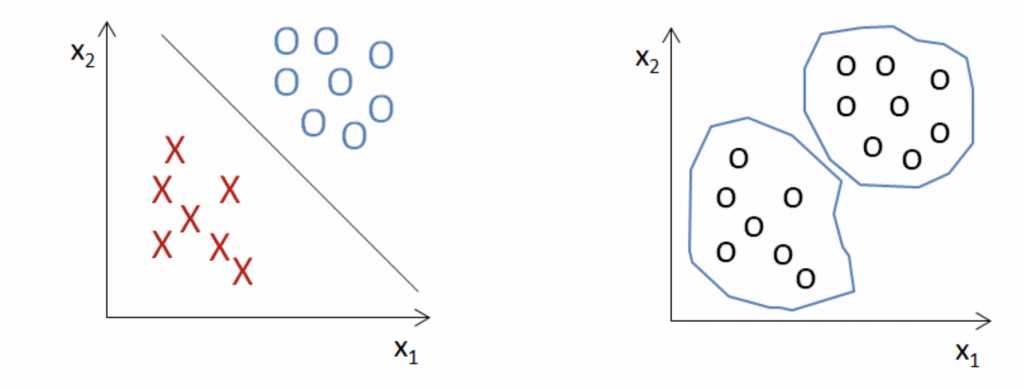

如果還聽不懂沒關係，下面我會舉一個簡單的例子，這個例子是我看到某位大大他在介紹K-Means時所舉的例子（機器學習: 集群分析 K-means Clustering）：
K-means Clustering這個方法概念很簡單，一個概念「物以類聚」。男生就是男生，女生就是女生，男生會自己聚成一群，女生也會自己聚成一群。
但在這群男生自己不會動成一群，女生也不會動成一群，在機器學習內，我們有的就是一組不會動的身高和體重的資料。那是什麼會動，讓男生女生可以區隔開的是什麼? 回頭看看演算法的名字，k-means，這邊的k是你想分成幾群，means就是每一群群心（ cluster centroid），所以會動的東西就是群心。這邊很懸，什麼是會動的群心??????
如果用實際的例子說，大家到新學校上學的時候有沒有一種感覺，第一天到的時候基本上大家都不熟，一個兩個人是一群，後來慢慢會有一群人聚在一起，沒幾天就分成兩群、三群，慢慢的到上學後一個月，基本上班上的小團體都分好了，每個團體都有一個key-man，你可以把這個key-man當作是群心，基本上大家都是因為有這個key-man聚在一起的(如果變節又是另一件事情)。那這個key-man在開學到小團體分好之前，基本上有可能會一直換來換去的，甚至多出一個key-man或是少一個key-man(演算法:ISODATA)，或是這個團體的key-man會因為別人的強勢而換掉，這就是會動=換掉的群心。

K-Means運作
假如手上擁有沒有label的資料，我們想將它分成兩類：

1. 決定把資料分成k群
2. 在二維平面上隨機選取 2 個點，稱爲 cluster centroid
3. 對每個資料都計算與這兩個cluster centroid的距離（歐基李德距離Euclidean distance），取比較近的距離，並把它歸為該群(cluster assignment)
4. 接著重新計算cluster centroid的位置（因為每次都會有被分類過來的資料）
5. 一直重複3、4，直到所有群cluster centroid沒有太大的變動才結束。

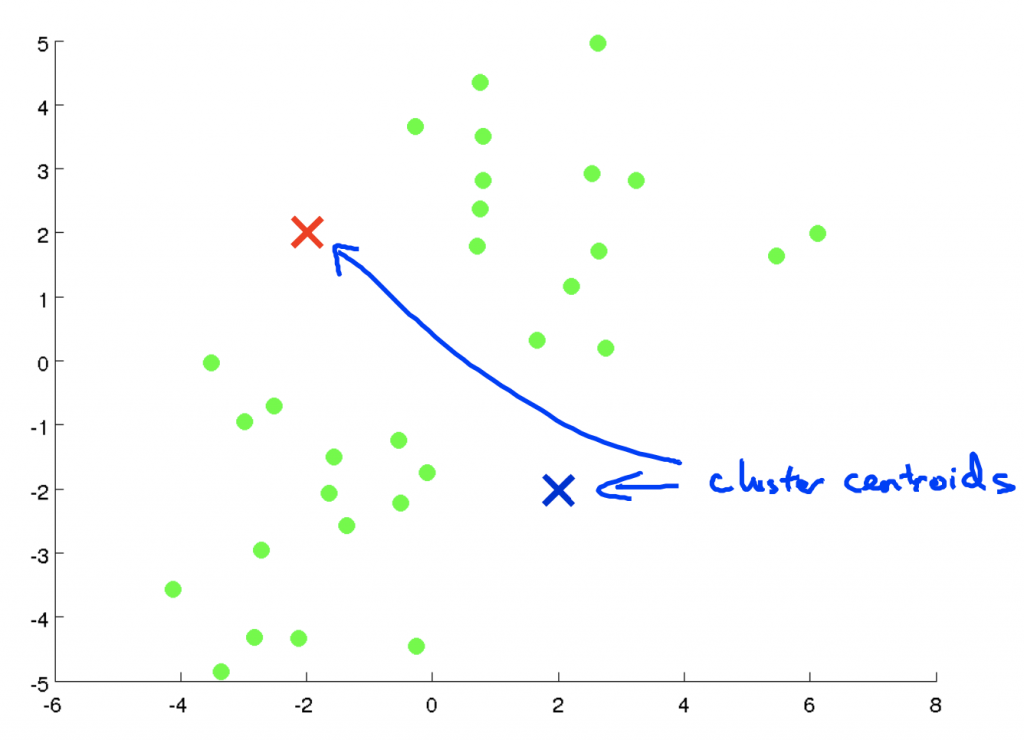
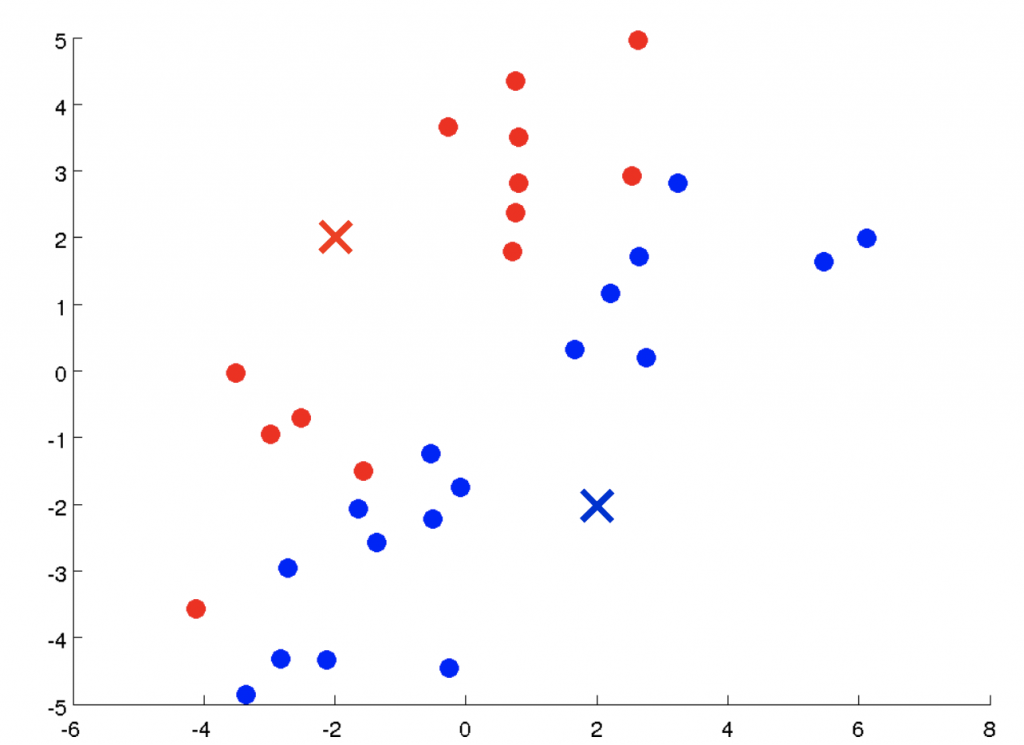
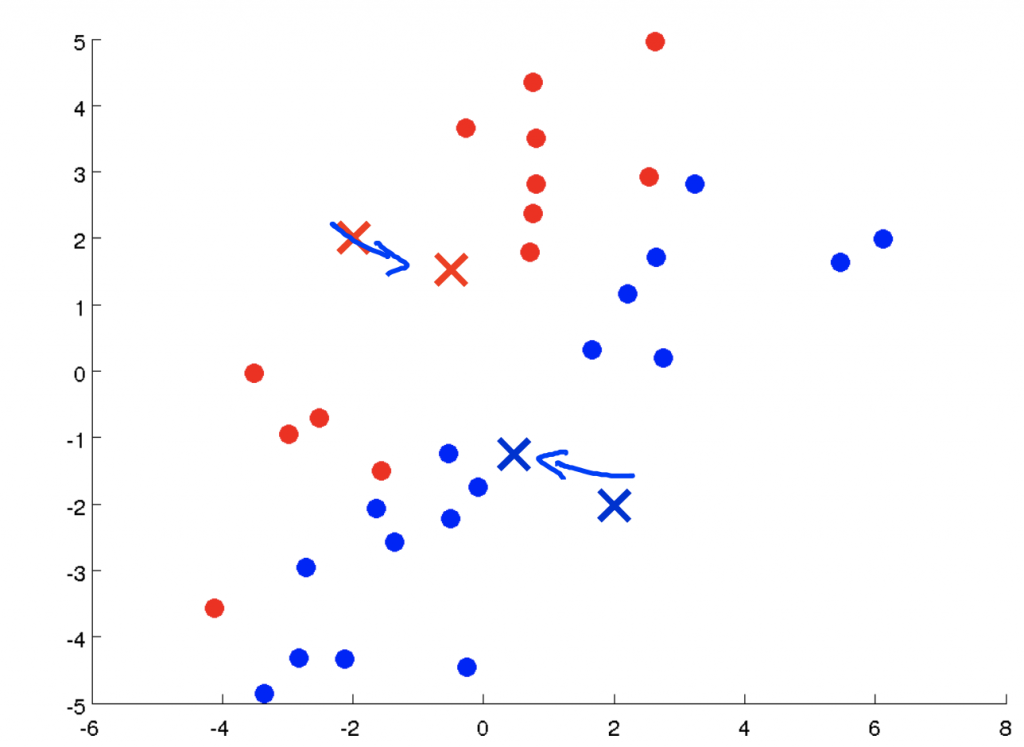
K-Means Algorithm
這裡的式子可以搭配上面幾張圖看。首先針對每個資料求與μ(cluster centroid)的距離，來找出每筆資料屬於哪個分群。

之前再介紹其他方法時都有目標函數來判斷最佳值，就是loss function，這邊也可以透過目標函數distortion function來判斷：

其實這個式子跟上面第一個for loop一模一樣，所以其實在做分群時計算每一個資料屬於哪一個群時，就是在取目標函數的最小值。第二個for loop是更新μ的值，就是把同群的放在一起，其實這樣做就可以把目標函數變小。所以這兩個for loop就是在對目標函數做最佳化。

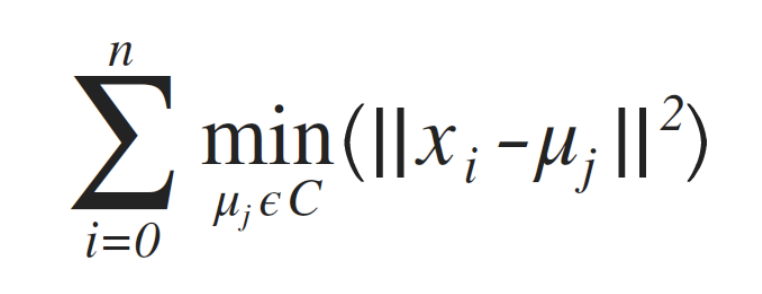
Random Initialization
初始所選定的μ的不同，會導致得到不同 clustering 的結果， 可能導致 local optima，⽽非 global optima。

所以比較好的做法是，Random Initialization的次數要多一點，找出目標函數最小時的μ來當作一開始所選定的cluster centroid

K-Means實作

import numpy as np
import matplotlib.pyplot as plt
import numpy as np

cl_num = 3
data_num = 20
thr = [0.00001, 0.00001, 0.00001]


def dist(x, y, mu_x, mu_y):
    return ((mu_x - x)**2 + (mu_y - y)**2)


def cluster(x, y, mu_x, mu_y):

    cls_ = dict()
    for i in range(data_num):
        dists = []
        for j in range(cl_num):
            distant = dist(x[i], y[i], mu_x[j], mu_y[j])
            dists.append(distant)
        cl = dists.index(min(dists))
        if cl not in cls_:
            cls_[cl] = [(x[i], y[i])]
        elif cl in cls_:
            cls_[cl].append((x[i], y[i]))

    return cls_


def re_mu(cls_, mu_x, mu_y):
    new_muX = []
    new_muY = []

    for key, values in cls_.items():

        if len(values) == 0:
            values.append([mu_x[key], mu_y[key]])

        sum_x = 0
        sum_y = 0
        for v in values:
            sum_x += v[0]
            sum_y += v[1]

        new_mu_x = sum_x / len(values)
        new_mu_y = sum_y / len(values)

        new_muX.append(round(new_mu_x, 2))
        new_muY.append(round(new_mu_y, 2))
    return new_muX, new_muY


def main():

    x = np.random.randint(0, 500, data_num)
    y = np.random.randint(0, 500, data_num)

    mu_x = np.random.randint(0, 500, cl_num)
    mu_y = np.random.randint(0, 500, cl_num)

    cls_ = cluster(x, y, mu_x, mu_y)

    new_muX, new_muY = re_mu(cls_, mu_x, mu_y)

    while any((abs(np.array(new_muX) - np.array(mu_x)) > thr)) != False or any(
        (abs(np.array(new_muY) - np.array(mu_y)) > thr)) != False:
        mu_x = new_muX
        mu_y = new_muY
        cls_ = cluster(x, y, mu_x, mu_y)
        new_muX, new_muY = re_mu(cls_, mu_x, mu_y)

    print('Done')

    plt.scatter(x, y)
    plt.scatter(new_muX, new_muY)
    plt.show()

    colors = ['r', 'b', 'g']
    for key, values in cls_.items():
        cx = []
        cy = []
        for v in values:
            cx.append(v[0])
            cy.append(v[1])
        plt.scatter(cx, cy, color=colors[key])

    plt.show()


if __name__ == '__main__':
    main()

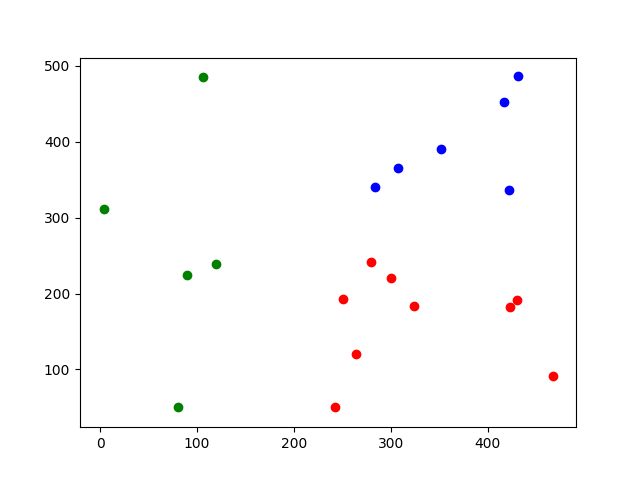
下面這張圖，藍色點是隨機產生的資料，橘色點是cluster centroid（經過多次計算找出最合適的）

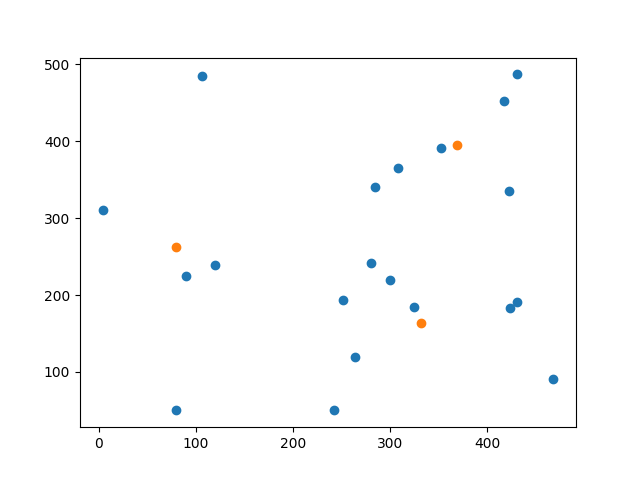
計算出每個點與cluster centroid的距離，並用不同顏色將其歸類。