今天是不寫程式改來學知識第二集,首先我們要先來說明坐標系統的奧妙,這邊不會講到非常數學,但會比一般的科普文章還深入一點,大家如果讀得下去就努力理解吧!
後面我們會引用proj4來進行坐標轉換,這部分很簡單應該不能算寫程式吧(?
地球為一個不規則的球體,沒辦法直接計算每一點的位置,因此為了要給予位置一個坐標,定義了與地球非常接近的旋轉橢球(非三軸橢球),可以以數學的方法來簡單表示。
而球體的定義也有非常多種,同一個球體不同的投影方式也造成了不同的坐標,因此我們現在就要來探討坐標系統之間的關係。
| 坐標系統 | EPSG | 橢球 | 狀態 |
|---|---|---|---|
| WGS84 | 4326 | WGS84 | 大地坐標 |
| Web Mercator | 3857 | WGS84 | 投影坐標 |
| TWD97 TM2 | 3826 | GRS80 | 投影坐標 |
| TWD67 | - | GRS67 | 投影坐標 |
有做過坐標轉換的應該都知道TWD67和其他任何一種坐標系統都不能直接轉,平平一樣都是坐標,有沒有想過為什麼會這樣呢?這就要從它的橢球特性說起了。
橢球體就是一個可以用數學方法來簡單表示,並在幾何形狀上和物理性質上都與大地體接近。是採用兩極稍扁的旋轉橢球面形成的橢球體來代替大地水準面,此橢球體稱為地球橢球體。
又分為總橢球體與參考橢球體。(也可以統稱參考橢球體)
與大地體外型相符合的地球橢球為總地球橢球體平均地球橢球,滿足以下三個條件:
總質量等於地球的總質量、中心與地球重心相合、赤道平面與地球赤道面相合。旋轉角速度與地球的旋轉角速度相等。體積與大地體的體積相等,表面與大地水準面之間的差距為平方和最小。也就是說總橢球體最符合整個地球的實體,但相對的不見得對於每個地方區域都很符合。WGS84、GRS80等橢球體都是屬於這種。
參考橢球體只與某一個國家或某一地區的大地水準面符合較好的地球橢球體,因此中心通常不與地球重心相合。
在參考橢球體初步定位時,橢球面和大地水準面之間有一個公切點,稱作大地原點;大地原點的坐標值就是國家坐標的起算值。
GRS67橢球體為參考橢球體與地表切於南投縣埔里虎子山,為大地基準點。
標準的坐標轉換方式是將
大地坐標轉換為直角坐標系(笛卡兒坐標系),再依據橢球參數進行轉換。
而直角坐標系若是使用總橢球體的話,則是地心地固坐標系ECEF;相對地若為參考橢球體的話,則為參心地固坐標系。
所以大家有注意到了嗎,因為TWD67的橢球GRS67是屬於參考橢球體,無法同樣轉換為地心地固坐標系,其橢球體的定位定向皆不一樣,無法直接進行轉換。
至於要如何將TWD67和其他的坐標系統進行轉換?將會在Day15說明使用控制點,進行平差解算轉換參數後將整批坐標轉換過去的方法。
我們無法在平面的紙上,以不變形的方式來表示三維的地球情形,因此投影是必須的,而只要有投影,就一定有誤差和變形。
我們在討論變形之前,可以先玩玩看下面兩個網站,先讓大家了解到我們常常看到地圖造成了許多人多大的誤解。
萬年不變的考題:格陵蘭和非洲大陸哪一個比較大?
使用不同的投影方式產生出的地圖
再次強調一次:投影一定有變形,沒有任何一種投影是最好的,而是取決於用途;以下分別以投影的性質來進行說明。
麥卡托投影、蘭伯特圓錐投影。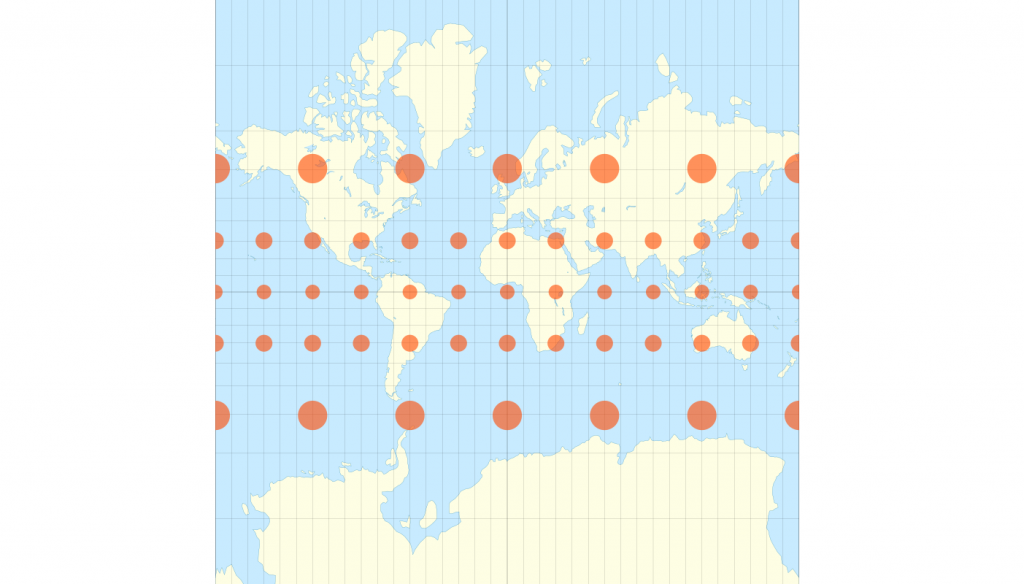
莫爾威投影、正弦曲線投影。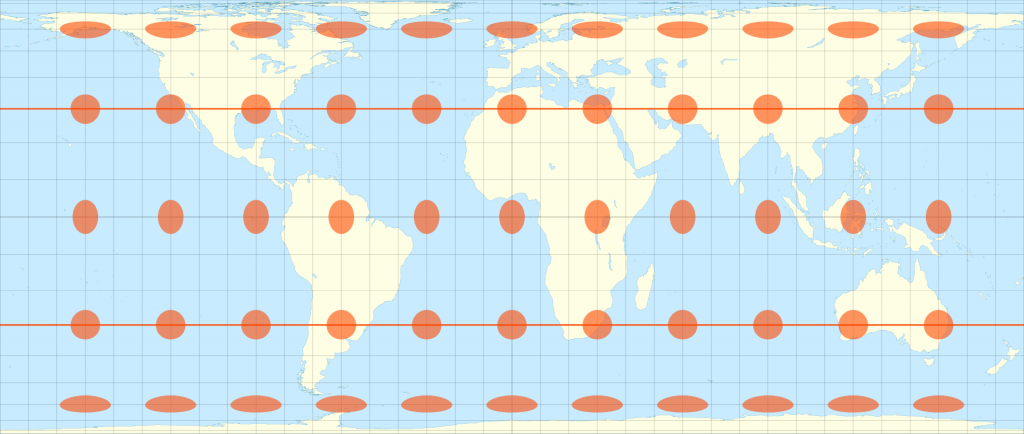
羅賓森投影、溫克爾投影。一點各方向或兩點間的尺度因子維持為1.0,但只有沿這些點上距離維持不變,稱為標準點。等距方位投影、等距圓錐投影。因為這邊用到了蠻多的投影坐標的,首先先來介紹橫麥卡托TM投影。
| 坐標系統 | 中央經度 | 中央經線尺度比 | 坐標偏移 |
|---|---|---|---|
| 2度 | 121E | 0.9999 | 250000m |
| 3度 | 121E | 1 | 350000m |
| 6度 | 123E | 0.9996 | 500000m |
中央經線:圓柱面與地球相切的子午面,若為相切,此條線變形量最小。中央經線尺度比(Scale Factor):若相切密合,則尺度為1,但圖面其他地方變形量很大;為讓尺度均勻,讓中央經線尺度略小於1,逐漸往兩側放大。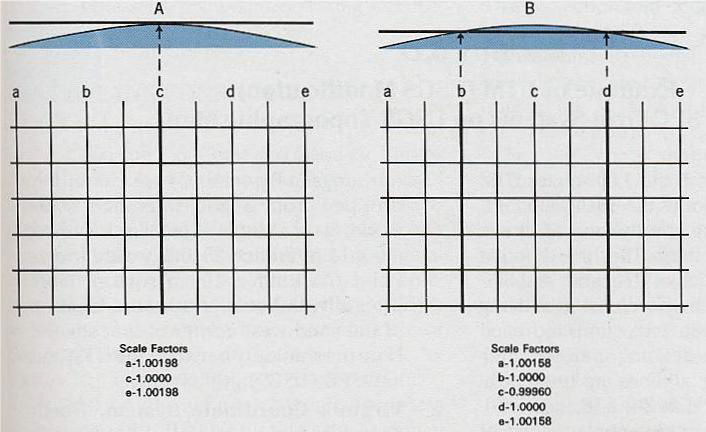
橫坐標平移量:為了避免讓中央經線西側坐標出現負數,而將投影坐標加一個常數。建立大地基準,就是求定旋轉橢球的參數(如長軸半徑a和短軸半徑b等)及其定向(橢球旋轉軸平行於地球的旋轉軸,橢球的起始子午面平行於地球的起始子午面)和定位(旋轉橢球中心與地球中心的相對關係)。
| 坐標系統 | WGS84 | Web Mercator | TWD97 | TWD67 |
|---|---|---|---|---|
| EPSG | 4326 | 3857 | 3826 | - |
| 參考橢球體 | WGS84 | WGS84 | GRS80 | GRS67 |
| 長半徑(m) | 6378137 | 6378137 | 6378137 | 6378160 |
| 扁率 | 1/298.257223563 | 1/298.257223563 | 1/298.257222101 | 1/298.25 |
| 投影 | 無 | 近似正球體轉換 | TM2 | TM2 |
| 參考框架 | - | - | ITRF1984 | - |
| 大地原點 | 無 | 無 | 無 | 南投埔里虎子山 |
| 常用 | Geojson等經緯度坐標 | WMTS通用坐標 | 臺灣測量常用的坐標 | 臺灣以前測量常用坐標 |
由上述的表可知,WGS84和TWD97的橢球是不一樣的!!!
曾經看過某間測量儀器公司的規格文章寫:WGS84與TWD97的地球原子相同,二者的形狀大小完全一樣,不是"很像",而是完全一模一樣!
前面講了一堆其實只是要讓大家知道坐標是如何定義的、是如何進行轉換的。
這邊我們使用proj4的這個js套件來進行坐標轉換,在WebGIS的系統開發上絕對會用到!
這邊先打個岔,要強烈的跟大家說絕對不要用Javascript來做浮點數的運算!!!它會有一些不知名的小數點在裡面。
0.1*0.2 //0.020000000000000004
0.2+0.1 //0.30000000000000004
題外話結束,首先我們先引入proj4js
<script type="text/javascript" src="js/Plug_in/proj4.js"></script>
觀察proj4的寫法,它首先需要先定義坐標系統,因此我們需要去查詢坐標參數,可以利用epsg.io 這個網站進行查詢。

輸入要查詢的坐標系統後,一路點選下去,往下拉找到Proj4js,複製裡面的內容(現在大家應該都看得懂裡面的參數的意義了吧!)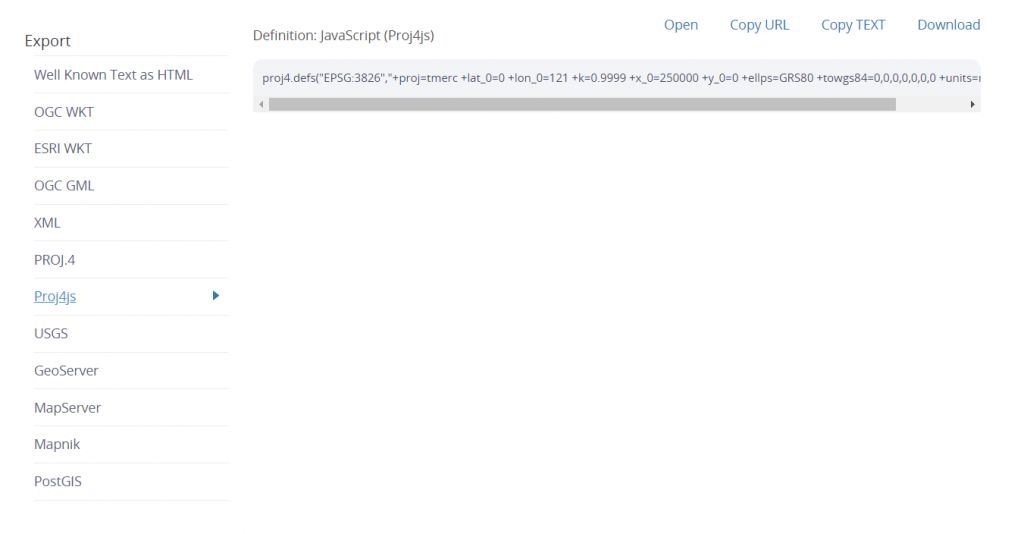
定義坐標系,將常用的4326、3826、3857都加入定義中,並且進行Openlayers的註冊
proj4.defs("EPSG:4326", "+proj=longlat +datum=WGS84 +no_defs");
proj4.defs("EPSG:3826", "+proj=tmerc +lat_0=0 +lon_0=121 +k=0.9999 +x_0=250000 +y_0=0 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs");
proj4.defs("EPSG:3857", "+proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +wktext +no_defs");
ol.proj.proj4.register(proj4);
假設我現在有一個點[121,25]是WGS84的坐標,想要將它轉換成Web Mercator,方式如下:
// 定義一個feature,直接在新增point之前將坐標進行轉換
// proj4(現在的坐標系統,欲轉換過去的坐標系統,[x,y])
var projfeature = new ol.Feature({
geometry: new ol.geom.Point(proj4("EPSG:4326","EPSG:3857",[121,25])),
name: 'projtest'
});
var projlayer = new ol.layer.Vector({
source: new ol.source.Vector({
})
});
map.addLayer(projlayer);
projlayer.getSource().addFeature(projfeature);
建立幾個測試數據,包含point、linestring、polygon、multipoint、multilinestring、multipolygon。
var wkt_point = "POINT(121 25)";
var wkt_linestring = "LINESTRING(121 25,121.5 25,121.5 25.5,121 25.5)";
var wkt_polygon = "POLYGON((121 25,121.5 25,121.5 25.5,121 25.5,121 25))";
var wkt_multipoint = "MULTIPOINT (10 40, 40 30, 20 20, 30 10)";
var wkt_multilinestring = "MULTILINESTRING ((40 40, 20 45, 45 30),(20 35, 10 30, 10 10, 30 5))";
var wkt_multipolygon = "MULTIPOLYGON (((40 40, 20 45, 45 30, 40 40)),((20 35, 10 30, 10 10, 30 5, 45 20, 20 35),(30 20, 20 15, 20 25, 30 20)))";
讀入WKT數據成feature,並同時進行坐標轉換
var format = new ol.format.WKT();
var feature_point = format.readFeature(wkt_point, {
dataProjection: 'EPSG:4326',
featureProjection: 'EPSG:3857'
});
var feature_linestring = format.readFeature(wkt_linestring, {
dataProjection: 'EPSG:4326',
featureProjection: 'EPSG:3857'
});
var feature_polygon = format.readFeature(wkt_polygon, {
dataProjection: 'EPSG:4326',
featureProjection: 'EPSG:3857'
});
var feature_multipoint = format.readFeature(wkt_multipoint, {
dataProjection: 'EPSG:4326',
featureProjection: 'EPSG:3857'
});
var feature_multilinestring = format.readFeature(wkt_multilinestring, {
dataProjection: 'EPSG:4326',
featureProjection: 'EPSG:3857'
});
var feature_multipolygon = format.readFeature(wkt_multipolygon, {
dataProjection: 'EPSG:4326',
featureProjection: 'EPSG:3857'
});
var wktlayer = new ol.layer.Vector({
source: new ol.source.Vector({
})
});
map.addLayer(wktlayer);
wktlayer.getSource().addFeature(feature_point);
wktlayer.getSource().addFeature(feature_linestring);
wktlayer.getSource().addFeature(feature_polygon);
wktlayer.getSource().addFeature(feature_multipoint);
wktlayer.getSource().addFeature(feature_multilinestring);
wktlayer.getSource().addFeature(feature_multipolygon);
假設我們現在的原始數據不是WKT,而是feature,也可以自定義一個helper的工具
var helper = function () {
proj4.defs("EPSG:4326", "+proj=longlat +datum=WGS84 +no_defs");
proj4.defs("EPSG:3826", "+proj=tmerc +lat_0=0 +lon_0=121 +k=0.9999 +x_0=250000 +y_0=0 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs");
proj4.defs("EPSG:3857", "+proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +wktext +no_defs");
return {
transOlGeometry: function (obj, transFunc) {
var geomJsonStr = JSON.stringify(obj.getGeometry().getCoordinates());
var tempgeom = JSON.parse(geomJsonStr);
var feature;
if (obj.getGeometry().getType() === "Point") {
tempgeom = transFunc(tempgeom);
feature = new ol.Feature({
geometry: new ol.geom.Point(tempgeom),
name: obj.getGeometryName()
});
} else if (obj.getGeometry().getType() === "MultiPoint") {
tempgeom.map(function (coorpair) {
return transFunc(coorpair);
});
feature = new ol.Feature({
geometry: new ol.geom.MultiPoint(tempgeom),
name: obj.getGeometryName()
});
} else if (obj.getGeometry().getType() === "LineString") {
tempgeom.map(function (coorpair) {
return transFunc(coorpair);
});
feature = new ol.Feature({
geometry: new ol.geom.LineString(tempgeom),
name: obj.getGeometryName()
});
} else if (obj.getGeometry().getType() === "MultiLineString") {
tempgeom = tempgeom.map(function (temparr) {
return temparr.map(function (coorpair) {
return transFunc(coorpair);
});
});
feature = new ol.Feature({
geometry: new ol.geom.MultiLineString(tempgeom),
name: obj.getGeometryName()
});
} else if (obj.getGeometry().getType() === "Polygon") {
tempgeom = tempgeom.map(function (temparr) {
return temparr.map(function (coorpair) {
return transFunc(coorpair);
});
});
feature = new ol.Feature({
geometry: new ol.geom.Polygon(tempgeom),
name: obj.getGeometryName()
});
} else if (obj.getGeometry().getType() === "MultiPolygon") {
tempgeom = tempgeom.map(function (temparr) {
return temparr.map(function (temparr1) {
return temparr1.map(function (coorpair) {
return transFunc(coorpair);
});
});
});
feature = new ol.Feature({
geometry: new ol.geom.MultiPolygon(tempgeom),
name: obj.getGeometryName()
});
}
return feature;
},
epsg4326to3857: function (arr) {
return proj4("EPSG:4326", "EPSG:3857", arr);
},
epsg4326to3826: function (arr) {
return proj4("EPSG:4326", "EPSG:3826", arr);
},
epsg3826to3857: function (arr) {
return proj4("EPSG:3826", "EPSG:3857", arr);
},
epsg3826to4326: function (arr) {
return proj4("EPSG:3826", "EPSG:4326", arr);
},
epsg3857to3826: function (arr) {
return proj4("EPSG:3857", "EPSG:3826", arr);
},
epsg3857to4326: function (arr) {
return proj4("EPSG:3857", "EPSG:4326", arr);
},
transOlGeometry_4326to3857: function (obj) {
return helper.transOlGeometry(obj, helper.epsg4326to3857);
},
transOlGeometry_4326to3826: function (obj) {
return helper.transOlGeometry(obj, helper.epsg4326to3826);
},
transOlGeometry_3826to3857: function (obj) {
return helper.transOlGeometry(obj, helper.epsg3826to3857);
},
transOlGeometry_3826to4326: function (obj) {
return helper.transOlGeometry(obj, helper.epsg3826to4326);
},
transOlGeometry_3857to3826: function (obj) {
return helper.transOlGeometry(obj, helper.epsg3857to3826);
},
transOlGeometry_3857to4326: function (obj) {
return helper.transOlGeometry(obj, helper.epsg3857to4326);
}
};
}();
最後呼叫helper進行轉換
var feature_linestring4326 = helper.transOlGeometry_3857to4326(feature_linestring)
今天大家學習了坐標系統的基本知識,並且知道了怎麼利用proj4套件進行坐標轉換。
明天我們就要實用這個套件,進行定位功能的建置。
