前一篇介紹了強化學習初步的概念,並且採隨機策略測試一下,隨機等於沒有策略,這次我們實際擬定一些策略,說明強化學習的真正作法。之後再介紹各種演算法的進化及其原由。
上一篇採隨機策略測試,結果很慘,因此,這次先不管強化學習,擬定一個策略測試看看是否可以過關,即行動超過200步。
擬定策略邏輯如下:
直接拿前篇程式28_02_cartpole_random.py 稍作修改即可,程式名稱為29_01_cartpole_deterministic.py,以下只列出有修改的部分:
class Agent:
# 初始化
def __init__(self):
self.direction = left
self.last_direction=right
# 自訂策略
def act(self, observation):
# cart_position:台車位置(Cart Position)
# cart_velocity:台車速度(Cart Velocity)
# pole_angle:平衡桿角度(Pole Angle)
# pole_velocity:平衡桿速度(Pole Velocity At Tip)
cart_position, cart_velocity, pole_angle, pole_velocity = observation
'''
行動策略:
1. 設定每次行動採一左一右,盡量不離中心點。
2. 平衡桿角度偏右8度以上,就往右前進,直到角度偏右小於8度。
3. 反之,偏左也是同樣處理。
'''
if pole_angle < math.radians(max_angle) and pole_angle > math.radians(-max_angle):
self.direction = (self.last_direction + 1) % 2
elif pole_angle >= math.radians(max_angle):
self.direction = right
else:
self.direction = left
self.last_direction = self.direction
return self.direction
agent = Agent()
while True:
# 依策略行動
action = agent.act(observation) #env.action_space.sample()
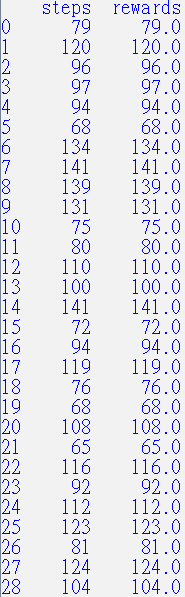
原來只能走20~40步,現在大都可以走100多步,雖然還是沒有贏,但是已經有大幅進步了,Yelp !
且慢,以上策略不是強化學習,因為:
以下,我們就來介紹強化學習的理論基礎,進而了解各項演算法。

圖一. 強化學習機制
圖一是一個不斷循環的機制,如果以S代表狀態(State),A代表行動(Action),R代表獎勵(Reward),那強化學習的軌跡(trajectory)如下: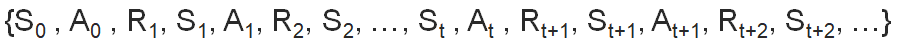
代理人如果思慮很周延,每次行動時都會考慮之前的軌跡,例如下棋,要決定下一步棋,會先考慮之前下的每一個位置,同時也會考慮對手的每一步棋,但是,考慮那麼久遠,模型就太複雜了,於是學者就提出【馬可夫決策過程】(Markov Decision Processes, MDP),假設決定行動時,只要考慮前面N個狀態,這就是【馬可夫性質】(Markov Property),通常N=1。
另外,強化學習的最佳行動目標是追求【長期累計報酬】(Return)最大化,而不是追求短期利益(Immediate Reward),例如下象棋,不管你吃對方多少棋子,最後【將/帥】被對方吃了,這盤棋就算輸了。因而【長期報酬最大化】的目標就創造出強化學習最偉大的公式 -- Bellman Equation。以下就從專門術語的定義,逐步推演出 Bellman Equation。
報酬(Return) Gt是從目前位置走到終點所獲得的累計獎勵,其中,γ(gamma)為折扣率,獎勵隨著時間打折扣,避免報酬變成無窮大。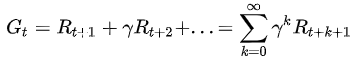
例如,走迷宮的遊戲,要從Start走到Goal,為儘速走到終點,所以定義每走一步的獎勵為負1,越快走到終點分數越高,一旦走到終點後,我們就可以從終點倒算出路徑每一格的報酬(Gt)。
圖二. 迷宮每一個位置的報酬(Gt)
狀態值函數(Value Function or State Value Function)是某一個狀態隱含的報酬期望值(E),例如走迷宮遊戲,到達終點的路徑有很多種,除了最短路徑,有些可能繞遠路,所以,每一格報酬期望值(E)就等於每一條有經過該格的路徑,倒算出來的報酬期望值。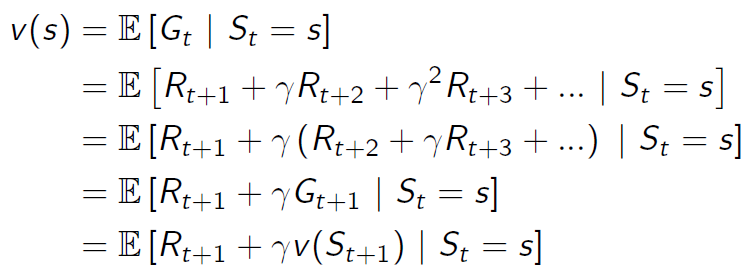
上式展開來: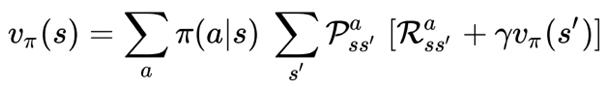
圖三. 狀態值函數公式
其中:
狀態值函數的計算是一種策略評估(Evaluation),我們可以測試各種策略π(a|s),得到最佳的策略,簡寫成下列方程式: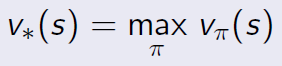
行動值函數(Action Value Function)是在狀態s時,採取特定行動(a)的報酬期望值。與狀態值函數類似,公式展開如下,有點複雜,故以圖(Backup Diagram)說明: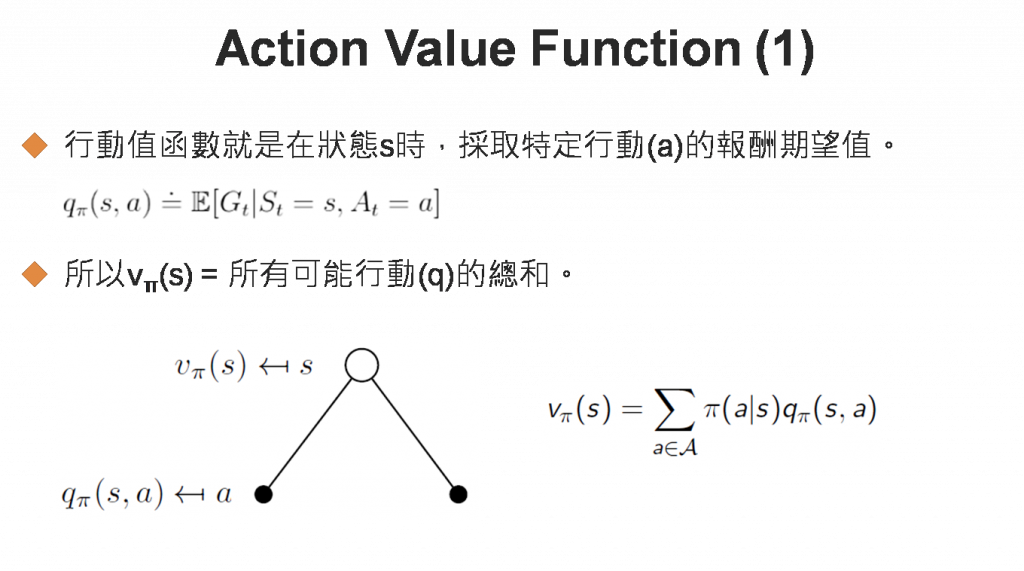

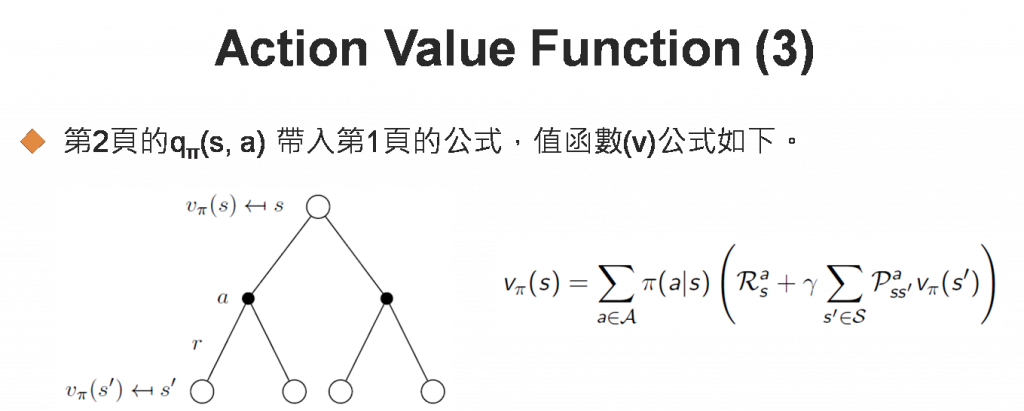
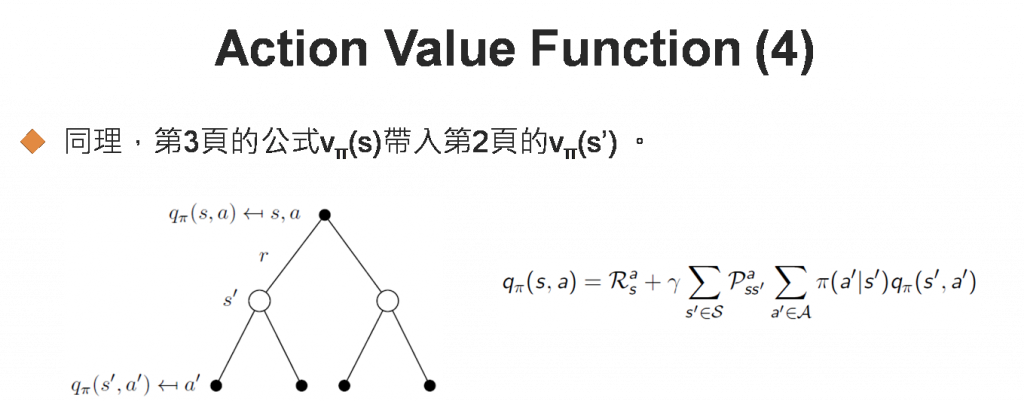

圖四. 行動值函數公式
以上投影片修改自David Silver大神的pdf。
在既定策略下,我們可以得到每一個位置的值函數,之後實際玩遊戲時,我們就可以採取一些戰術,例如貪婪(Greedy)戰術,每次都選擇最大值函數的狀態,以改善目前的策略,簡寫成下列方程式: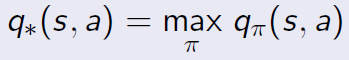
所以,如果依照以下循環學習,稱為策略迭代(Policy Iteration):
(1) 策略評估(Policy evaluation):先使用確定性的(deterministic)策略π(a|s),估計每一個位置的狀態值函數,確定性的(deterministic)策略通常是一機率分配,如均勻(Uniform)分配、Poisson分配...等。
(2) 策略改善(Policy improvement):再依照貪婪(Greedy)或其他戰術,選擇最有利的位置行動。在每個位置走下一步後,回到步驟(1),重新計算所有位置的狀態值函數。一直迭代下去,直到策略不再變動為止,即最佳行動的選擇與目前策略完全一致。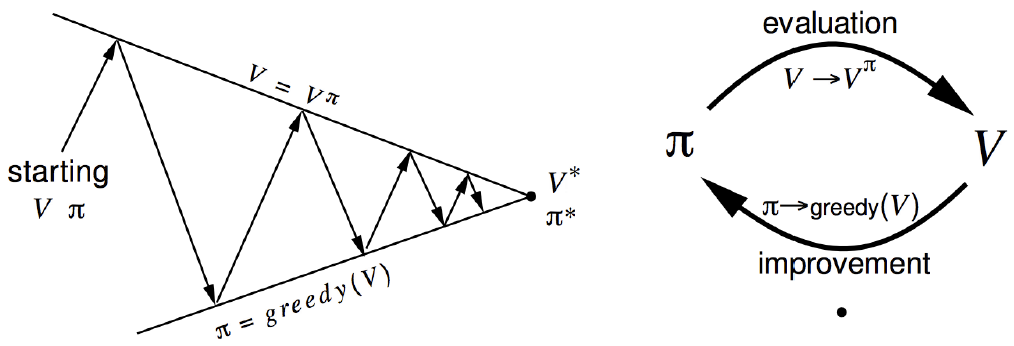
圖五. 策略迭代(Policy Iteration)
個人認為,策略迭代的過程與梯度下降法很像,一開始先以隨機策略開始,計算出狀態值函數(正向傳導),之後採取各種戰術(類似優化器),例如貪婪(Greedy)或ε-Greedy戰術,更新狀態值函數(反向傳導),直到最佳解找到為止。
講到這裡,大家應該一個頭兩個大了,我們以走迷宮的遊戲為例說明,澄清以上觀念。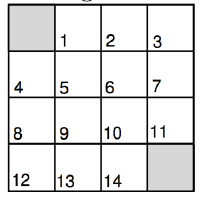
圖六. 迷宮遊戲
遊戲規則如下:
策略評估計算過程如下:
經過不斷的循環,最終的狀態值函數如下圖左表,依照貪婪戰術,每一個位置可行的方向也出爐了,如下圖右表。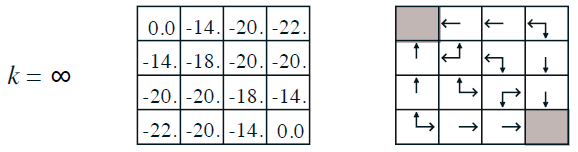
圖七. 迷宮遊戲最終的狀態值函數
程式修改自【Denny GitHub】,程式名稱為29_02_Policy_Evaluation.ipynb:
from IPython.core.debugger import set_trace
import numpy as np
import pprint
import sys
from lib.envs.gridworld import GridworldEnv
pp = pprint.PrettyPrinter(indent=2)
env = GridworldEnv()
def policy_eval(policy, env, discount_factor=1.0, theta=0.00001):
"""
policy: [S, A] shaped matrix representing the policy.
env.P:狀態轉移機率矩陣
env.P[s][a]:(prob, next_state, reward, done) 陣列
env.nS:狀態總數
env.nA:行動總數
theta: 狀態值函數變動 <= theta,即停止進行。
discount_factor: 獎勵折扣率(Gamma)
傳回【狀態值函數】
"""
# 一開始【狀態值函數】均為 0
V = np.zeros(env.nS)
while True:
delta = 0
# For each state, perform a "full backup"
for s in range(env.nS):
v = 0
# 執行每一種可能的行動
for a, action_prob in enumerate(policy[s]):
# 行動可能到達的每一種狀態
for prob, next_state, reward, done in env.P[s][a]:
# 計算【狀態值函數】期望值,參考圖三. 狀態值函數公式
v += action_prob * prob * (reward + discount_factor * V[next_state])
# 找出每一個位置的這一輪與上一輪狀態值函數差異最大者
delta = max(delta, np.abs(v - V[s]))
V[s] = v
# 最大差異 < 事先設定值 theta,則停止評估
if delta < theta:
break
return np.array(V)
# 隨機策略,每一個位置往上、下、左、右走的機率均為 0.25。
random_policy = np.ones([env.nS, env.nA]) / env.nA
# 策略評估
v = policy_eval(random_policy, env)
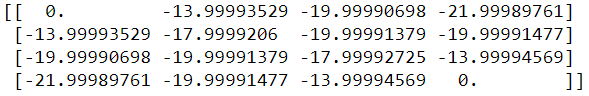
程式修改自【Denny GitHub】,程式名稱為29_03_Policy_Iteration.ipynb,囿於篇幅,只列出關鍵段落:
def policy_improvement(env, policy_eval_fn=policy_eval, discount_factor=1.0):
"""
policy_eval_fn: 策略評估函數。
discount_factor: 獎勵折扣率(Gamma)
Returns:
傳回 (policy, V) 陣列.
- policy:是最佳策略, [S, A] 二為矩陣,含每個狀態/行動組合的機率分配.
- V:狀態值函數。
"""
# 走下一步的處理,計算行動值函數
def one_step_lookahead(state, V):
"""
state: 狀態值
V: 狀態值函數
傳回【行動值函數】
"""
A = np.zeros(env.nA)
# 圖四. 行動值函數公式
for a in range(env.nA):
for prob, next_state, reward, done in env.P[state][a]:
A[a] += prob * (reward + discount_factor * V[next_state])
return A
# 隨機策略,每一個位置往上、下、左、右走的機率均為 0.25。
policy = np.ones([env.nS, env.nA]) / env.nA
while True:
# 策略評估
V = policy_eval_fn(policy, env, discount_factor)
# 策略是否趨於穩定的旗標
policy_stable = True
# 每一個狀態均採貪婪戰術
for s in range(env.nS):
# 貪婪戰術
chosen_a = np.argmax(policy[s])
# 走下一步的處理,計算行動值函數
action_values = one_step_lookahead(s, V)
# 找出最大行動值函數
best_a = np.argmax(action_values)
# 貪婪戰術 不等於 最大行動值函數,繼續迭代
if chosen_a != best_a:
policy_stable = False
policy[s] = np.eye(env.nA)[best_a]
# 策略趨於穩定就結束訓練
if policy_stable:
return policy, V
policy, v = policy_improvement(env)
print("Policy Probability Distribution:")
print(policy)
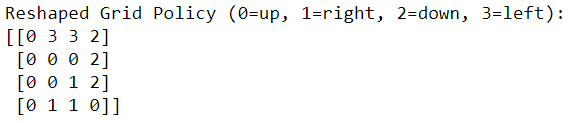
圖八. 策略迭代:在每個狀態的最佳行動
策略迭代(Policy Iteration)假設初始採用隨機策略,值迭代(Value Iteration)不設定明顯的策略,直接利用圖四【行動值函數公式】迭代,找出策略。
程式名稱為29_04_Value_Iteration.ipynb,囿於篇幅,只列出關鍵段落:
def value_iteration(env, theta=0.0001, discount_factor=1.0):
"""
env.P:狀態轉移機率矩陣
env.P[s][a]:(prob, next_state, reward, done) 陣列
env.nS:狀態總數
env.nA:行動總數
theta: 狀態值函數變動 <= theta,即停止進行。
discount_factor: 獎勵折扣率(Gamma)
Returns:
傳回 (policy, V) 陣列.
- policy:是最佳策略, [S, A] 二為矩陣,含每個狀態/行動組合的機率分配.
- V:狀態值函數。
"""
def one_step_lookahead(state, V):
"""
state: 狀態值
V: 狀態值函數
傳回【行動值函數】
"""
A = np.zeros(env.nA)
for a in range(env.nA):
for prob, next_state, reward, done in env.P[state][a]:
A[a] += prob * (reward + discount_factor * V[next_state])
return A
V = np.zeros(env.nS)
while True:
delta = 0
# 每一個狀態均採貪婪戰術
for s in range(env.nS):
# 走下一步的處理,計算行動值函數
A = one_step_lookahead(s, V)
# 找出最大行動值函數
best_action_value = np.max(A)
# 找出每一個位置的這一輪與上一輪狀態值函數差異最大者
delta = max(delta, np.abs(best_action_value - V[s]))
# 更新值函數
V[s] = best_action_value
# 最大差異 < 事先設定值 theta,則停止評估
if delta < theta:
break
# 再作一次,產生 policy
policy = np.zeros([env.nS, env.nA])
for s in range(env.nS):
# 走下一步的處理,計算行動值函數
A = one_step_lookahead(s, V)
best_action = np.argmax(A)
# 設定目前狀態下最佳的行動
policy[s, best_action] = 1.0
return policy, V
policy, v = value_iteration(env)
print("Policy Probability Distribution:")
print(policy)
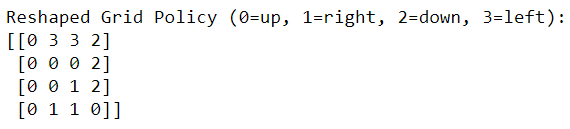
圖九. 值迭代:在每個狀態的最佳行動
結果與策略迭代相同。
本篇介紹了強化學習最偉大的公式 -- Bellman Equation,並利用公式設計兩種迭代 -- 策略迭代(Policy Iteration)、值迭代(Value Iteration),自我學習找出最佳策略,其實這就是所謂的【動態規劃】(Dynamic Programming)的演算法,這種解法不僅可自我學習,也具通用性,如果套用到其他遊戲上,幾乎不需要更改程式碼。
但是,以上演算法有太多的假設,不符合現實:
因此後續發展出很多的演算法克服以上的假設,洋洋灑灑如下所列:
以上列表來自【denny GitHub】,有志者可繼續努力挖掘了。
本篇範例包括 29_01_cartpole_deterministic.py、29_02_Policy_Evaluation.ipynb、29_03_Policy_Iteration.ipynb、29_04_Value_Iteration.ipynb 以及 Lib 目錄,可自【這裡】下載。
