資料結構的部份快到尾聲了,今天會聊聊雜湊,光從文字上來看就非常抽象,不知道是什麼意思,就讓我們一起來揭開它的神秘面紗吧!
你有用過果汁機嗎?
圖片來源:freerangestock
我們只要將各式各樣、雜七雜八的蔬果通通丟入果汁機,經過處理之後,最後都會變成壓榨液體,這種物品 A 透過某些處理之後變成物品 B 的例子還有哪些呢?
像是研磨器,把各式各樣、雜七雜八的堅果丟進去,最後會被磨小變成粉末,那物品 B 可以變回物品 A 嗎?要說一句經典老話:回不去了XD,所以電腦科學中蠻常使用這種方式在幫我們的帳戶密碼做加密,因為只有你自己知道要丟入哪些堅果,才能不斷的製造出特殊成分的粉末,其它人只看看到那堆粉末,無法猜到原始的材料
雜湊從字面上的意思來說,就是將原始資料,透過一種特殊複雜的公式,湊成另一種格式
上述的果汁機或研磨機,就像特定公式,會將原始資料運算為其它的資料,我們可以將運算完的結果拿去做額外的利用
資料 A 透過某個公式轉換成資料 B
蠻多都會用在加密或驗證的領域,像是:
身分證字號
我們的身分證字號不能隨便亂打,有些系統在用戶輸入身分證字號時,會去驗證身分證是否為合法的字串,那個驗證的公式大家可以自己 google 看看
MD5 演算法(Message-Digest Algorithm)
是一種密碼雜湊函式,可以到這個網站 http://www.md5.cz/ 將文字輸入,按下 hash 按紐就會得到另一串文字,像是輸入test就會得到098f6bcd4621d373cade4e832627b4f6,但雜湊是不可逆的,無法從 098f6bcd4621d373cade4e832627b4f6 反推回 test,如果今天輸入tesa,只差一個字,但得到的雜湊值會長得完全不一樣,所以 MD5 常常用來儲存用戶的密碼,系統不會保存使用者原始的密碼,因為這樣資料庫如果被駭客侵入,密碼就會被知道,所以一般來說會將密碼以 MD5 加密後再存入資料庫,等下次用戶登入輸入密碼時,再將密碼做 MD5 運算,將其結果跟資料庫的內容比對即可,這樣的做法相對安全,因為只有用戶自己才會知道他自己的原始密碼為何,如果今天用戶忘記密碼,就請用戶重新設定即可,因為系統人員無法回推用戶的原始密碼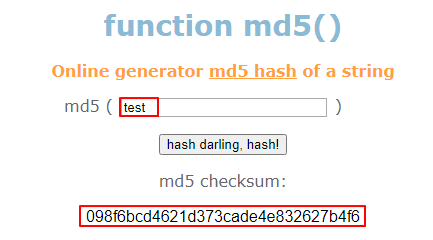
接著我們可以使用雜湊函數的特性,來協助我們儲存與尋找資料,接下來就皆紹一下雜湊法
是一種資料儲存與搜尋的一種方式,要存取資料之前,要先經過額外的計算,才知道要將資料存放在哪裡,或是要去哪裡讀取資料
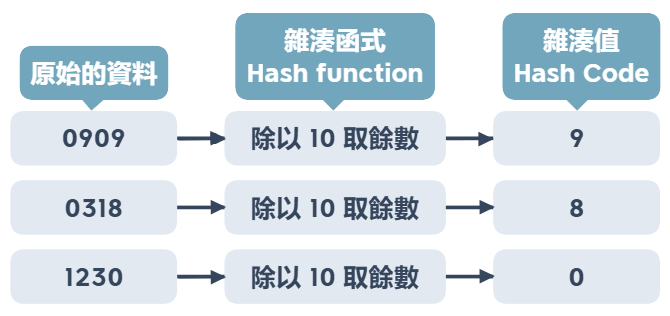
例如有一個客人的生日為 0909, 將 0909 代入特定公式,像是 909 除以 10 取餘數 就會得到 9 ,然後就將這筆資料歸檔到 9 號櫃子,而 9 號櫃子就是我們找資料的關鍵,下次客人來我們將他的生日代入特定公式,就能知道他的資料存在哪裡,另外也可以發現,光是看櫃子的號碼,我們是無法回推櫃子內的出生月份有哪些,而這個特定公式有個專有名詞就稱為雜湊函數 (Hashing Function)
雜湊函數 (Hashing Function)
將資料透過特定的計算方式,計算出來的結果可轉換成資料儲存的位址,好的雜湊函數應計算簡單,少碰撞,讓雜湊表的儲存狀況能平均
雜湊值 (Hash Code)
原始資料 x 經過雜湊函數 H 所計算的結果,H(x) = Hash Code,計算出來的結果無法回推原始資料,為不可逆
雜湊表 (Hash Table)
為連續的記憶體,用來儲存資料,每一筆資料會對應到一個位置 (Bucket)
桶 (Bucket)
雜湊表中的某一筆資料,會存放在某一個位址 (Bucket Address)
槽 (Slot)
一筆資料會有好幾各欄位,例如:一筆資料有 2 個欄位,則代表桶中有 2 個槽
碰撞 (Collision)
若多筆資料經過雜湊函數的雜湊值皆相同,則會使用到同一個桶位址(Bucket Address)
溢位 (Overflow)
資料經過雜湊函數的計算後,雜湊值所指向的桶位址已經被其它資料存滿,此筆資料無法儲存在該位址
常見的有4種,用來計算數值適合存放再陣列中哪一個位置
除法 (Mod /Division)H(x) = x mod B,將 x 代入函式,x 除以 B 取餘數,即為雜湊值,例如,數字 20 要存入有 7 個位置陣列中,H(20) = 20 mod 7,會得到 6 ,則 20 這個數值,會被放到陣列 6 的位置中
中間平方法 (Middle Sequare)
假設我們有 100 個儲存空間,將數值加工一下,數值 * 數值,就是數值平方的意思,然後取某一段的數字做為儲存位置,例如數字 13 取平方後13 * 13 = 169,取十位數與個位數會得到 69 ,所以就可以在陣列位置 69 中存放 13 這個數值
折疊法 (Folding Addition)
此法又區分成兩種方法:
移動折疊法 (Shift)
如果今天要處理的數值很大,是好幾位的數字,則可自行拆成多個區段,例如,數字 842384518,則可以將拆成 3 個區塊 842 + 384 + 518 = 1744
邊界折疊法 (Boundary)
將基數段或偶數段反轉後再加相,可減少碰撞,例如,可將上例的偶數段 384 反轉成 483,然後重新相加 842 + 483 + 518 = 1843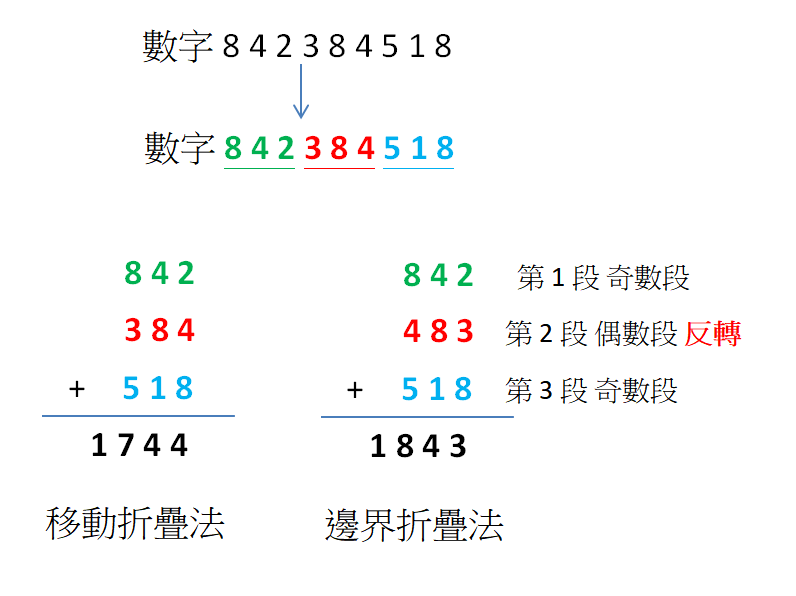
數位分析法 (Digits Analysis)
如果已知資料的相似度很高,則可將重覆的資料捨去,例如手機號碼,都是 09 開頭,則 09 的部分就不需要參與計算,可挑選某一段具特殊意義的數字來做運算
以上這四種雜湊函數可自己根據情況使用,並沒有規定一定要怎麼做,但有一個狀況需要特別注意,就是當多筆計算出來的儲存位置皆相同的時候,也就是所謂的溢位,一起來看看要怎麼處理吧
線性探測 (Linear Probing) / 線性開放定址 (Open Addressing Mode)
當兩筆資 x 與 y,代入雜湊函式 H(x) 與 H(y) 之後,若得到相同的雜湊值,則會發生溢位,此時可以將雜湊值依序 + 1,一格一格往後尋找有沒有其它空位,直到找到空位,或是儲存空間皆存滿為止
例如,今天有 4 位民眾,要儲存他們的年齡,各為 40、11,32,20,而雜湊函數使用除以 10 取餘數,逐一將透過雜湊函序運算後,就可以存到對應的位置,最後會發現當要存入 20 時,位置 0 已經存滿資料了,往後找位置 1 跟 2 也都滿了,找到位置 3 才找到空位,儲存狀況如下圖:mod 是取餘數的意思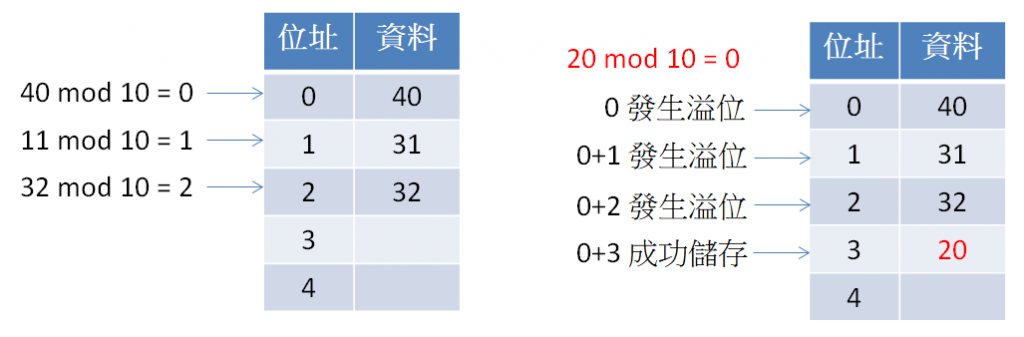
缺點:搜尋空位的時間不穩定,可能會有一堆資料存在附近,要往後找很久才找到空位
平方探測 (Quadratic Probing)
發生溢位時,使用 ,其中的 b 為資料可儲存的位置(Bucket Address)數量,i 是逐一遞增 i = 1,2,3,4,....,套入公式後,即可找到新的儲存位置,若還是發生溢位,則 i 繼續加 1 ,並代入公式
例如,今天有 4 位民眾,要儲存他們的年齡,各為 41、13,32,22,會發現處理 22 時發生溢位,而會開始套用平方探測的公式,如下圖:
缺點:若有一堆資料存在附近,要往前或找後找很久才找到空位
連結串列 (Chaining)雜湊表一開始會在每個位置準備各自的串列,同一個位置可存放多筆資料,以連結串列相接起來,例如,今天有 4 位民眾,要儲存他們的年齡,各為 41、13,32,22,在處理 22 時,就可將資料放在 32 後面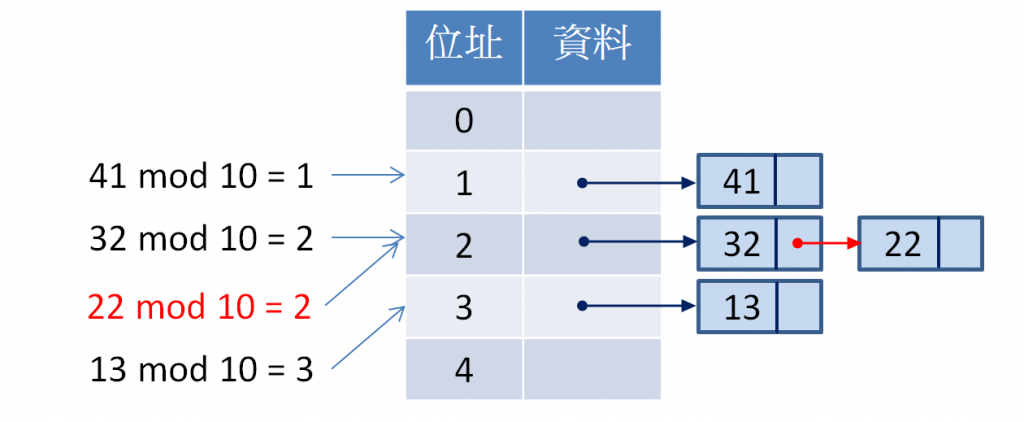
再雜湊 (Rehashing)
準備多個`雜湊函式,當第一種雜湊函式遇到溢位時,就換第二種雜湊函式,如果第二種雜湊函式遇到溢位時,就算第三種,直到沒有發生溢位為止
假設今天要統計班上的血型分佈,下面就以 C# 做為示範,在新增資料時,我們可以直接呼叫 Add 方法,事實上底層會幫我們去做資料的儲存與碰撞或溢位的處理,我們只需要透過現成的方法去操作資料即可,使用起來非常簡易
Hashtable hashTable = new Hashtable(); // 宣告一個 Hash Table 用來儲存資料
hashTable.Add("A 型", 5); // 輸入鍵值與內容
hashTable.Add("B 型", 6);
hashTable.Add("O 型", 12);
hashTable.Add("AB 型", 2);
輸出結果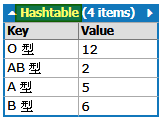
看完今天的文章可能會有點頭暈,基本上可以先掌握一個觀念,就是一個數值一定有屬於它的存放位置,那這個存放位置不是隨隨便便亂存的,是要根據某個雜湊函數所推估出來的,所以一個值除了他自己本身之外,我們還要知道這個值是被存在哪裡,就必須透過雜湊表去查詢,雜湊表包含索引位置跟數值,類似 key 與 value 的概念,只要我們透過雜湊函式得到 key ,則我們要取得 value ,就是輕而易舉的事情囉!
小美想傳一個訊息給男友,於是小美準備了:
H(x) = x mod B
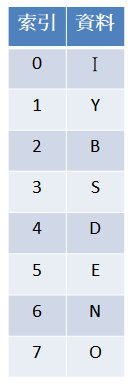
你能幫忙小美轉達嗎?
謎題說明:掌握相鄰串列 (Adjacency List)的要點之後就可以將圖形畫出來,但頂點之間的距離或位置,會因為每個人的畫法而有不同,所以長相會有點不太一樣,但只要符合相鄰串列中的關係,都是正確的,但因為謎題需要大家猜一樣禮物,而這樣禮物又是求婚必備的,女生看到會非常驚喜的東西,就需要把圖形再調整一下,就會發現,禮物是鑽石,你答對了嗎XD,這題似乎有點難