對圖形有基本的認識之後,我們要來了解圖形是如何被儲存的,就像二元樹會以陣列或串列儲存,那圖形會以什麼方式儲存呢,讓我們一起來看看吧
圖形表示法有四種,以下會逐一介紹
定義:
有一圖形,有 n 個頂點,則可利用 n * n 的 2 維陣列來表示,如下圖頂點有 4 個,則可以用 4 * 4 的二維矩陣表示,逐一觀察每個頂點與其它頂點有沒有邊,並套用下列規則填滿矩陣中的值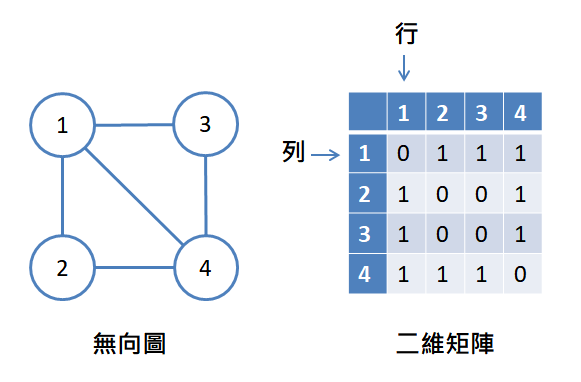
陣列的值與圖形的關係:
頂點 1與頂點 2之間有一條邊
頂點 3與頂點 2之間沒有邊
步驟:
頂點 1 與頂點 2、頂點 3 、頂點 4 之間都有邊,則將矩陣中的 [ 1, 2 ], [ 1, 3 ], [ 1, 4 ] 填 1頂點 2 與頂點 1、頂點 4 之間都有邊,則將矩陣中的 [2, 1 ], [ 2, 4 ] 填 1頂點 3 與頂點 1、頂點 4 之間都有邊,則將矩陣中的 [ 3, 1 ], [ 3, 4 ] 填 1頂點 4 與頂點 1、頂點 2、頂點 3 之間都有邊,則將矩陣中的 [ 4, 1 ], [ 4, 2 ], [ 4, 3 ] 填 1特性:
無向圖的矩陣是對稱的,即 [ 1, 2 ] = [ 2, 1 ],對角線皆為 0,有向圖則不一定
無向圖的矩陣是對稱的,所以只要保存矩陣的上三角或下三角即可,故可僅需 n ( n - 1 ) / 2 的空間分支度:
分支度就是第 i 列的元素和,例如:頂點 1 的分支度 = 0 + 1 + 1 + 1 = 3第 i 列的元素和,如下圖的頂點3,出分支度就是第 3 列的元素和 = 1 + 1 = 2第 i 行的元素和,如下圖的頂點3,入分支度就是第 3 行的元素和 = 1 + 0 + 0 = 1 ,另外下圖的矩陣不是對稱矩陣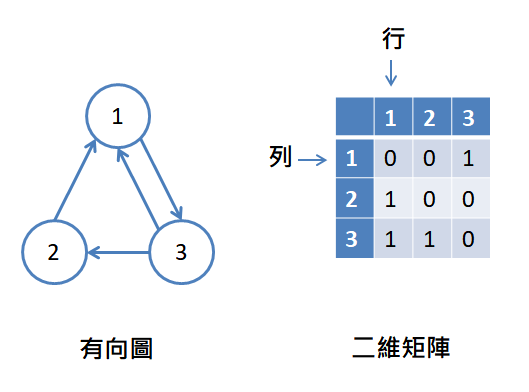
顧名思義,這個表示法就是以串列來儲存圖形,與相鄰陣列不同的是,串列只處理有邊的部分,沒有邊的部分不處理
定義:
有一圖形,每個頂點都有自己的串列,串列中的每一個節點用來儲存相鄰的頂點,每個節點包含兩個欄位:頂點與指向相鄰頂點的指標
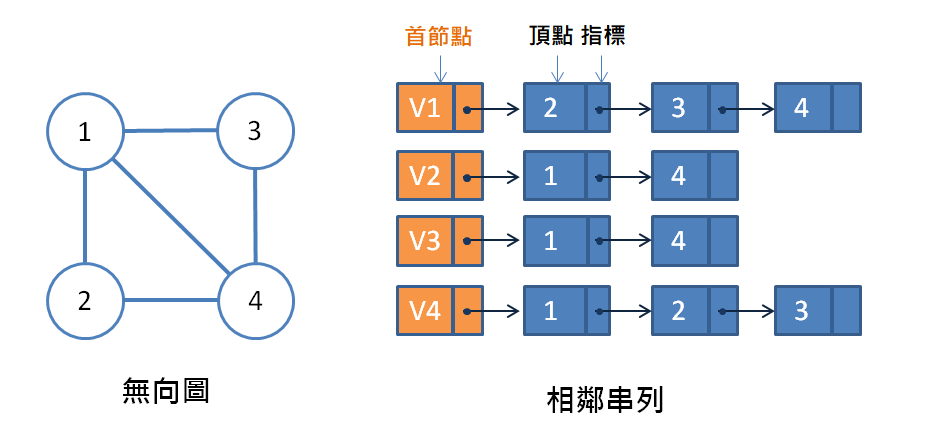
步驟:
頂點 1 ,其中與頂點 2、頂點 3 、頂點 4 之間都有邊,則在串列後方新增頂點 2、頂點 3 、頂點 4 的節點頂點 2 與頂點 1、頂點 4 之間都有邊,則在串列後方新增頂點 1、頂點 4 的節點頂點 3 與頂點 1、頂點 4 之間都有邊,則在串列後方新增頂點 1、頂點 4 的節點頂點 4 與頂點 1、頂點 2、頂點 3 之間都有邊,則在串列後方新增頂點 1、頂點 2、頂點 3 的節點特性:
無向圖若有 n 個頂點,e 個邊,則需要 n 個首節點與 2*e 個節點,例如上圖有 4 個頂點,與 5 個邊,則需要 4 個首節點與 10 個節點( 2 * 5 )有向圖若有 n 個頂點,e 個邊,則需要 n 個首節點與 e 個節點,例如下圖有 3 個頂點,與 4 個邊,則需要 3 個首節點與 4 個節點分支度:
上圖頂點 1 的串列,除了首節點之外,有 3 個節點,分支度為 3下圖頂點 3 的串列,除了首節點之外,有 2 個節點,分支度為 2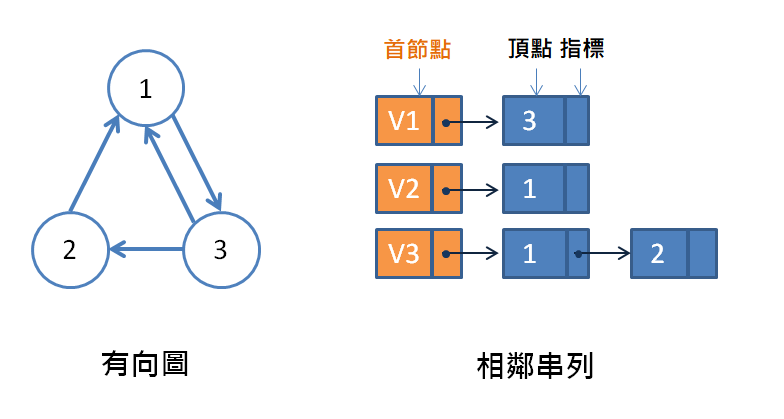
儲存無向圖型的一種方法,上述兩種都是針對頂點處理,這個方法為以邊為主
定義:
每個邊皆以一個節點表示,此節點包含:邊的標記、邊的起點、邊的終點與兩個指標可指向其它節點
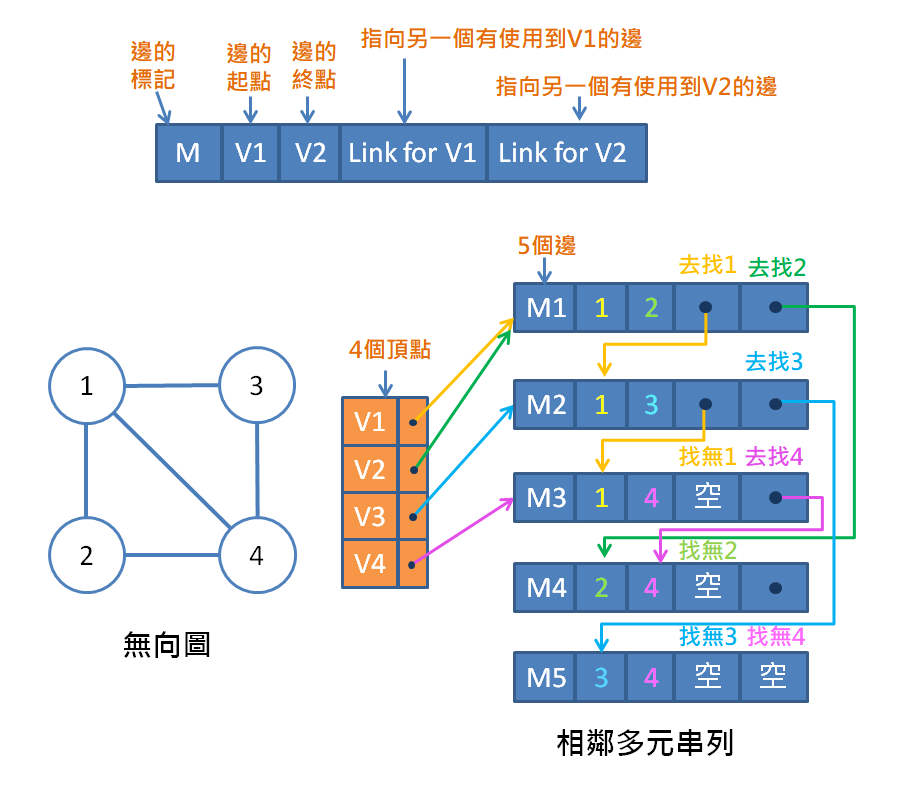
步驟:
每個節點用來儲存圖形中的每個頂點
所有的邊,並將每一個邊的起點與終點儲存在各自的串列之中第 1 步驟的節點(存放頂點)指向第一個包含此頂點的邊
兩個指標,將指標分別指向另一個包含此起點的邊,與另一個包含此終點的邊,以上圖 M1 的邊為例,此邊的起點為 1 則指標指向 M2,因為 M2 邊包含頂點 1,而 M1 邊的終點為 2 ,則指標指向 M4,因為 M4 的邊含有 M 2指標找不到邊可指向,則為空(null)使用兩個一維陣列依照順序儲存相鄰的頂點
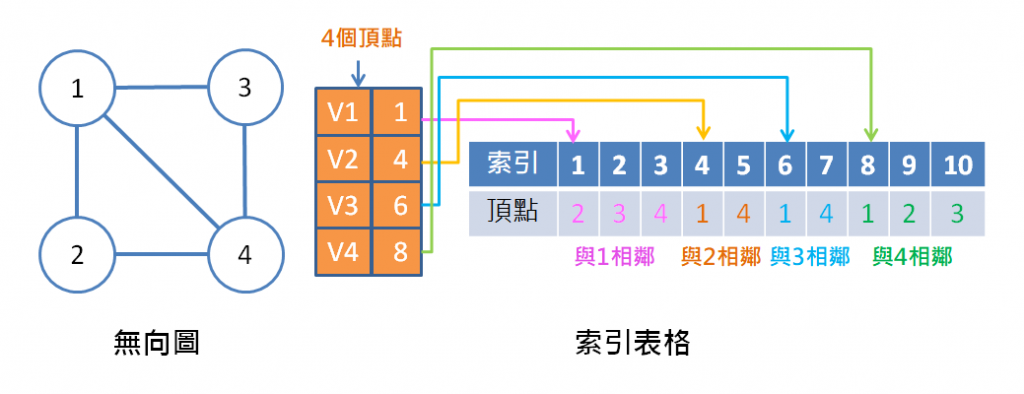
定義與步驟:
起始位置在哪裡,例如頂點 1,有3各相鄰頂點,而存放第一個相鄰頂點 2 的位置,是在此陣列的第 1 個索引四種表示法,都離不開之前說過的陣列與串列,如果不熟悉的話,可以往前翻閱,另外四種表示法各有其優缺點,例如相鄰矩陣在路經很少的情況下容易浪費空間,但求分支度就非常方便,而相鄰串列法比較節省空間,但求分支度時比較麻煩,還是要根據程式需求去做選擇
小美的男友準備跟小美求婚,於是準備了神秘超大驚喜要給小美,請問你能協助小美發現這份驚喜的禮物是什麼嗎?
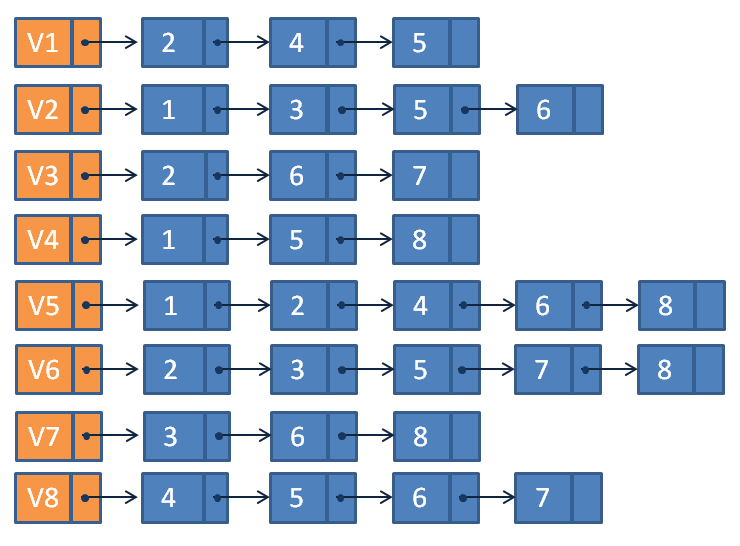
謎題說明:
V (所有頂點的集合): { W, B, C, D, E }
E (所有邊的集合): { ( W, B ), ( B, D ), ( D, E ), ( E, C ), ( C, W ) }
將頂點先圈起來,在將兩頂點之間的連線畫上去,就會發現五芒星的形狀,在仔細一看,兩邊交叉處都會經過一個字母,將五個字母集合起來,就會得到 GRAPH ,答案就是 GRAPH ,你答對了嗎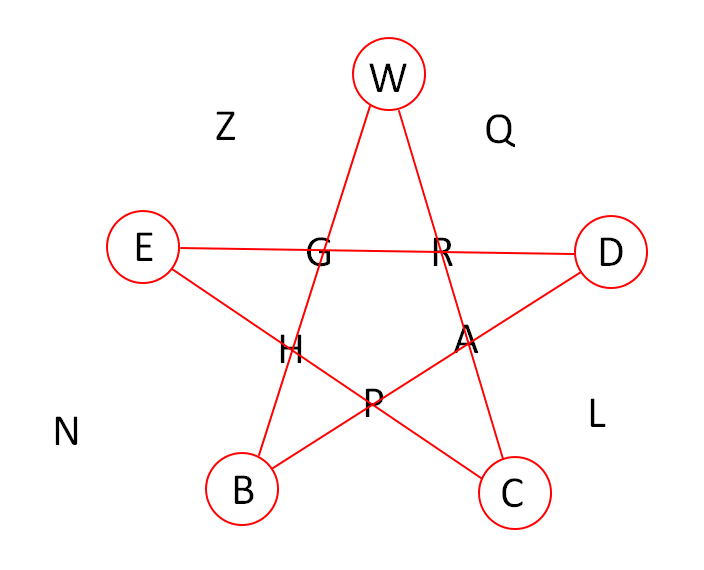

請問版主大大:
本文中,相鄰多元串列 (Adjacency Multilist)的圖,其中M4中的指標是不是要指向M5中的4,似乎缺少一個紫色箭頭?
https://d1dwq032kyr03c.cloudfront.net/upload/images/20200929/20129841c5TUcJnx8V.png
內文非常有幫助!謝謝