https://jerry-the-potato.github.io/Chapter4-demo3/
有了前兩篇作為基礎就更容易了!今天我們想做漩渦的動畫,讓一朵朵的花冒出並繞著畫面中心旋轉,那麼一樣給予初始條件:
switch(animeName){
case 'Falling':
this.beginX = Math.random() * WIDTH;
this.beginY = Math.random() * HEIGHT;
break;
case 'Floating':
this.beginX = Math.random() * WIDTH;
this.beginY = Math.random() * 0.1 * HEIGHT + 0.95 * HEIGHT;
break;
case 'Staring':
this.beginX = Math.random() * 0.1 * WIDTH + 0.45 * WIDTH;
this.beginY = Math.random() * 0.1 * HEIGHT + 0.45 * HEIGHT;
break;
}
雖然希望在中間,但位置也要稍微有所不同,因此設置寬高0.45-0.55之間,一個0.1x0.1的方格為起始點
一樣計算公轉角度(總算是個很直觀的簡諧運動了!)
let lT = this.lifeTime;
let revolveNow = this.revolveTheta + this.revolveOmega * dT / lT;
let A = Math.sin(revolveNow);
let B = Math.cos(revolveNow);
接著給定一個半徑,就可以用半徑和角度取得座標並旋轉了!
let radius = 0.3 * (WIDTH + HEIGHT);
this.pointX = this.beginX + radius * this.scaleX * (this.period * 0.5 * B - 0 * (dT / lT));
this.pointY = this.beginY - radius * this.scaleY * (this.period * 0.5 * A - 0 * (dT / lT));
數字0的部分一樣可以自行修改,為整體動畫添加線性軌跡
記得要去體驗一下今天風中的花兒,搭配規律、多樣、混亂、自由四種動畫效果唷,每種感受都很不一樣呢!
今天的部份真快結束!那就出個思考題吧,如果希望畫面真的像漩渦一般,讓花朵在旋轉的時候漸漸吸往中心點,可以怎麼做呢?提示:思考radius和時間的關係。
(當初第三章就有偷偷放一個其實不是demo的上來,裡面就有這個效果唷!)
開玩笑,怎麼能這樣草草結束呢?
仔細考量過後,還是來解釋一下好了!過往我們作的動畫都是基於sin和cos,其方便性大家應該都體會到了,唯一的問題就是說,如果圖案的縮放想要使用三角函數,就變成圖案大小變化的過程,只會在高峰值短暫停留,那使用者還沒機會看清楚圖案,圖案馬上又要消失了,這是我們不希望發生的,因此思路很簡單,我們的目的就是:「使其在高峰值停留更久」,具體要多久,起初是採用三等分切法,三分之一變大、三分之一停留高峰值、三分之一變小。
為了要達成這個目的,便要採用數線的距離公式,基本的公式是什麼?還記得國中有一種題目,叫做數線上有兩個點,分別是A和B,請試著取一個C點,使得C到AB距離的總和為最小值,這樣的C點有幾個?答案其實就是AB線段上的所有點,換句話說,只要C點位於AB線段時,其距離總和就是最小值,此時便是我們想要的穩定狀態;另一方面,當C點離開AB線段,離得越遠,C與AB的距離皆會增加,因此總和會一直無上限的增加。
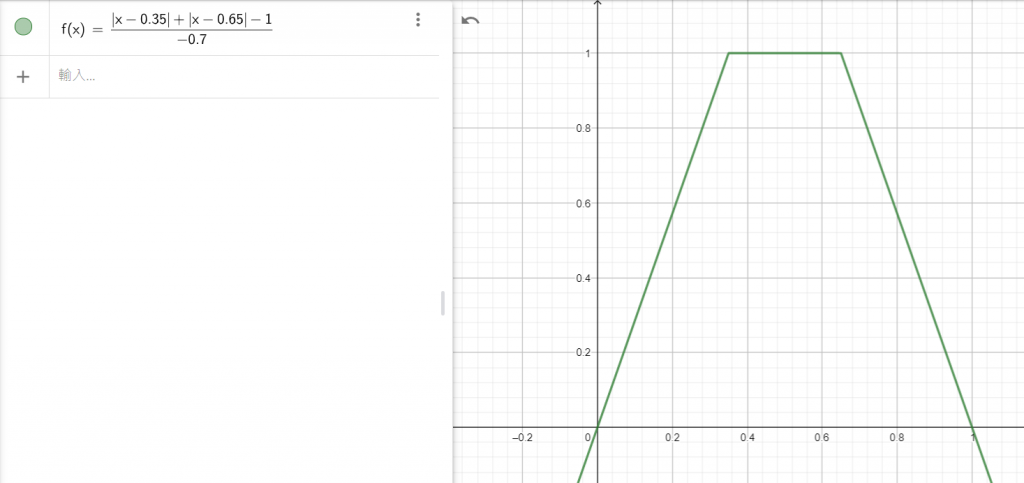
映射後的結果(物件大小變化圖)
上述也是前幾天給大家示範的做法,缺點是到穩定狀態後,那三分之一真的就停留在高峰值,大小完全不變,顯得有些不自然,今天我們再進行改良,並包成更容易調整的函式吧!
我們話不多說,接著就從程式開始撰寫,這次我們採用3個點的寫法,相比之下可以讓數線公式更接近於sin的平滑,又保留我們想要的穩定效果,公式為:Math.abs(t - t1) + Math.abs(t - t2) + Math.abs(t - t3);
為了讓大家好懂一些,我們先來套數字吧!
t表示輸入的值,我們設定為dT/lT,是昨天提到的一次性週期,從動畫開始0-1動畫結束,這邊我們分別設置對稱的三個點(0.35, 0.5, 0.65),使得公式成為:
Math.abs(t - 0.35) + Math.abs(t - 0.5) + Math.abs(t - 0.65);
以同樣的邏輯去推理,就可得知,在0~1之間,0和1是距離這三個點最遠的位置,0.5則是距離這三個點最近的位置,因此,可以寫成完整代碼:
let maxT = 0.5; // 預期圖案在此時最大 max
let minT = 0; // 預期圖案在此時最小 min
let t1 = 0.35;
let t2 = 0.5;
let t3 = 0.65;
let maxD = Math.abs(maxT - t1) + Math.abs(maxT - t2) + Math.abs(maxT - t3);
let minD = Math.abs(minT - t1) + Math.abs(minT - t2) + Math.abs(minT - t3);
這邊可能有人會感到疑惑,摁?你剛剛不是說0.5是最近的嗎?怎麼變成maxT了!別緊張,這裡指的是圖案的最大值(所映射的時間0.5),同理,maxD也是圖案的最大值(所映射的距離總和),什麼意思呢?
精確地說,這裡應該叫座標轉換,試想,如果今天輸入值是1到0,希望把輸出值改成0到1,可以怎麼映射呢?簡單,就寫:newX = 1 - oldX,就可以從舊的x座標轉換成新的x座標了,在這個例子中,既是把X軸作水平翻轉,又向右平移了1個單位,不過,映射厲害的地方在於,我們不一定要完全懂其中的原理,也可以輕鬆映射。
首先將目前的時間dT/lT輸入到公式,接著得到距離總和dist:
let dist = Math.abs(dT/lT - t1) + Math.abs(dT/lT - t2) + Math.abs(dT/lT - t3);
let transSize = (dist - minD) / (maxD - minD);
而原本dist介於minD到maxD之間,我們希望能作轉換,使其介於0-1之間,因此:
- 將其先減去最小值,使得dist介於0到(maxD-minD)之間
- 然後再除以(maxD-minD),就能使其介於0到1之間
代數很難懂吧qq,來我們代入數字,計算後得知minD為1.5、maxD為0.3,因此:
然後就沒有然後了,我們的功能就神奇的做完了!
但是,我們還是可以把公式寫得更好維護一些,如下:
let Distance = function(t, t1 = 0.35, t2 = 0.5 ,t3 = 0.65){
if(!isNaN(t))
return Math.abs(t - t1) + Math.abs(t - t2) + Math.abs(t - t3);
}
判斷輸入值t是否"不"為NaN或數字以外的值,並給予t1、t2、t3預設值,可輸入、可不輸入
animeObject.prototype.GetSize = function(dT, lT){
let maxD = Distance(0.5);
let minD = Distance(0);
let distance = Distance(dT/lT);
let transSize = (distance - minD) / (maxD - minD);
return transSize;
}
animeObject.prototype.Staring = function(dT){
// ......
// 以上省略
const popSize = 0.1;
this.sizeNow = WIDTH * this.size * (popSize + (1 - popSize) * this.GetSize(dT, lT));
}
說明:
圖片完整大小設為 WIDTH * this.size
popSize是初始的參數0.1
再加上0.9 * 剛剛公式回傳的transSize
這麼一來,就可以得到我們想要的曲線了: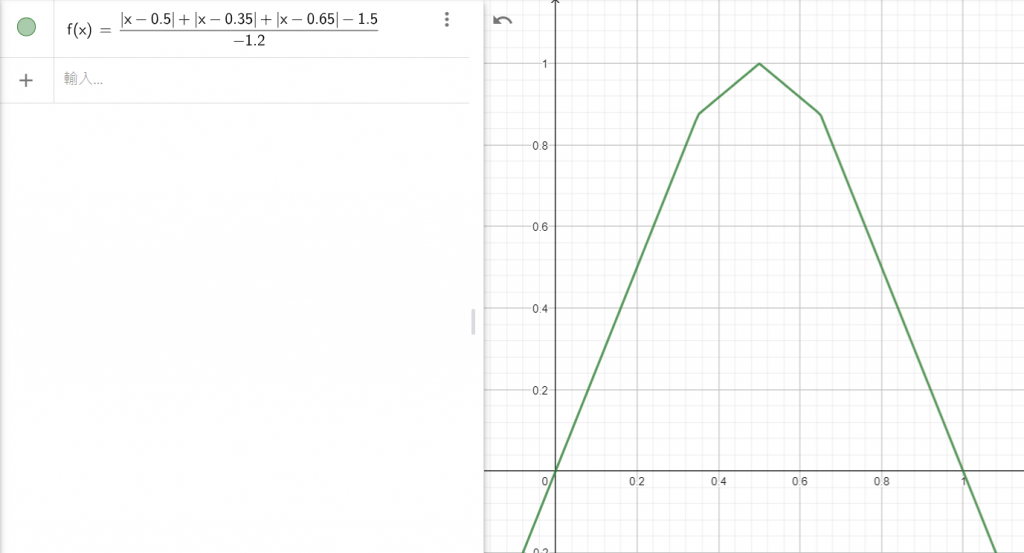
可以試著到geogebra複製這一行函數,即可看到上圖
f(x)=((abs(x-0.5)+abs(x-0.35)+abs(x-0.65)-1.5)/(-1.2))
不過,畢竟是折線圖,如果覺得變大變小的過程過於線性,可以給transSize次方項:return Math.pow(transSize, 0.6);
我蠻推薦0.6的,可以讓花朵快速長出來,並且在最大時停留更久,如圖: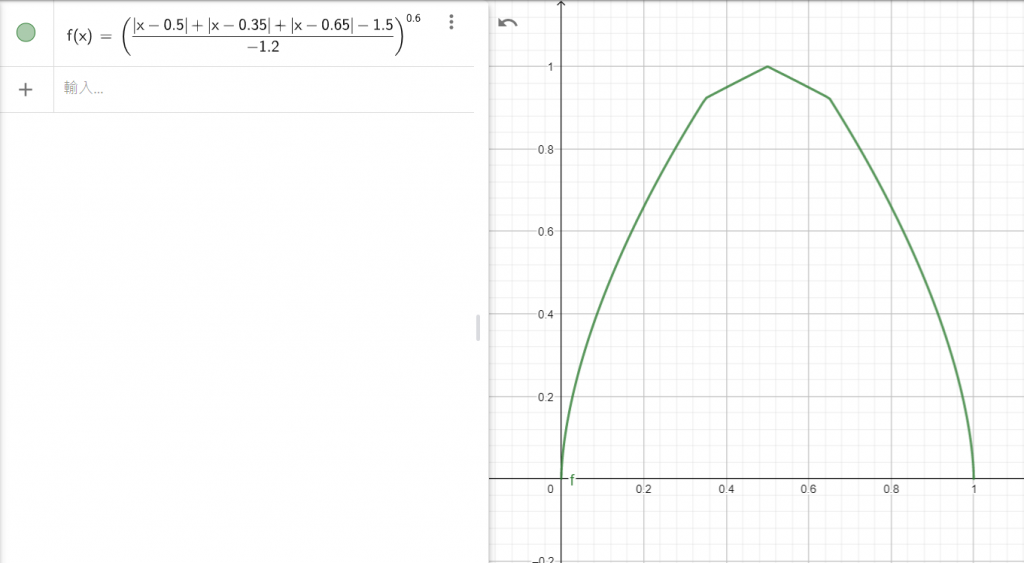
反過來說,也可以設置1.5,會使得花朵出來時,短暫的靜止不變,接著才快速長大,造成延遲效果,到最大時的變化也相對劇烈一些,是另一種感覺。
經過這次鐵人賽逐步整理,變得好簡潔(感動)