今日大綱
主成分分析是降維的其中一個演算法,它將較高維度的資料以較低維度的資料表示,解決了維度災難 (Curse of dimensionality)的問題,為非監督式學習。
降維後,會依據變數的重要性排序,因此有第一主成分、第二主成分…等,如果變數中每個資料都很接近,代表此變數較不重要;如果每個資料都不太相同,那麼這個變數可以表達資訊。
以下圖為例,橘色向量比綠色向量的重要性高,因為將資料點投影在橘色向量時,其能涵蓋大部分的資料,而綠色向量所能呈現的資訊量較橘色向量少。
選擇向量或超平面時主要有兩個指標:
決定變數重要性的為貢獻率,計算方式為特徵值除以全部變數特徵值之總和,每個變數從第一個主成分累加的貢獻率稱為累積貢獻率。
特徵提取與特徵選擇聽起來很像,很常會讓人搞混,它們之間的差別在哪?
進行特徵提取後的資料與原始資料不同,這個方法是將高維的資料以較低維度的資料表示,在保有原始特徵的前提下,以少量變數呈現許多變數的資料,盡可能保留原始資料的特性。
特徵選擇後的資料與原始資料相同,其作法是在多個特徵裡選取幾個特徵保留,進行訓練。Lasso regression就是linear regression的目標裡增加一個逞罰項,最小化所有權重絕對值之合,迫使某些較不重要的特徵權重為0,這就是特徵選擇。
主成分分析主要有三個步驟:
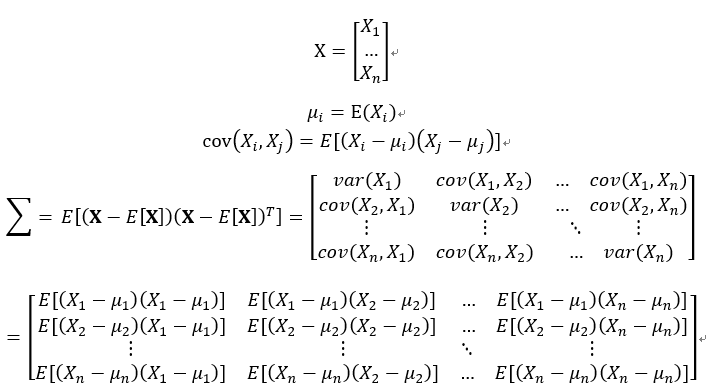

今天使用的資料集是鳶尾花,利用花瓣的長度、寬度,以及花萼的長度寬度判斷為哪種品種的鳶尾花。
首先匯入資料,並且分成目標變數與自變數。
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = load_iris()
x = pd.DataFrame(data['data'])
x.columns = data['feature_names']
y = pd.DataFrame(data['target']).values
接著使用PCA取得各個特徵的特徵值,這裡我將主成分設為2
從第三行程式碼可以看到,在訓練時不需要目標變數,因為他是非監督式學習。
n_components = 2
pca = PCA(n_components = n_components)
pca = pca.fit(x)
transformed = pca.transform(x)
呼叫explained_variance_ratio_取得兩個成分的貢獻率
var_exp=pca.explained_variance_ratio_ #獲得貢獻率
np.set_printoptions(suppress=True) #當suppress=True,表示小數不需要以科學計數法的形式輸出
print('各主成分貢獻率:',var_exp)
cum_var_exp=np.cumsum(var_exp) #累計貢獻度
print('各主成分累積貢獻率:',cum_var_exp)
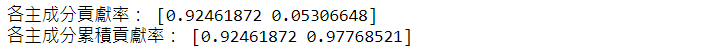
從結果可看出,第一個主成分的貢獻率遠高於第二個貢獻率。通常到第五個主成分後,貢獻率非常的為小。
程式碼已上傳至我的Github
Machine Learning – Feature Selection vs Feature Extraction
共變異數矩陣
特徵值和特徵向量
sklearn 庫的 PCA 如何檢視貢獻率
感謝您的瀏覽,我們明天見!![]()
