今日大綱

• 神經網路簡介
• 梯度下降法 (Gradient descent)
• 激活函數 (Activation function)
• 程式碼

神經網路簡介

下圖為簡單的神經網路圖，隱藏層為兩層以上即稱為深度學習。如果激活函數 (Activation function)都為線性函數，一個神經網路可以視為多個線性回歸所組成，但現實生活中的例子皆為非線性的，因此需要經過其他的激活函數轉換，並預測結果。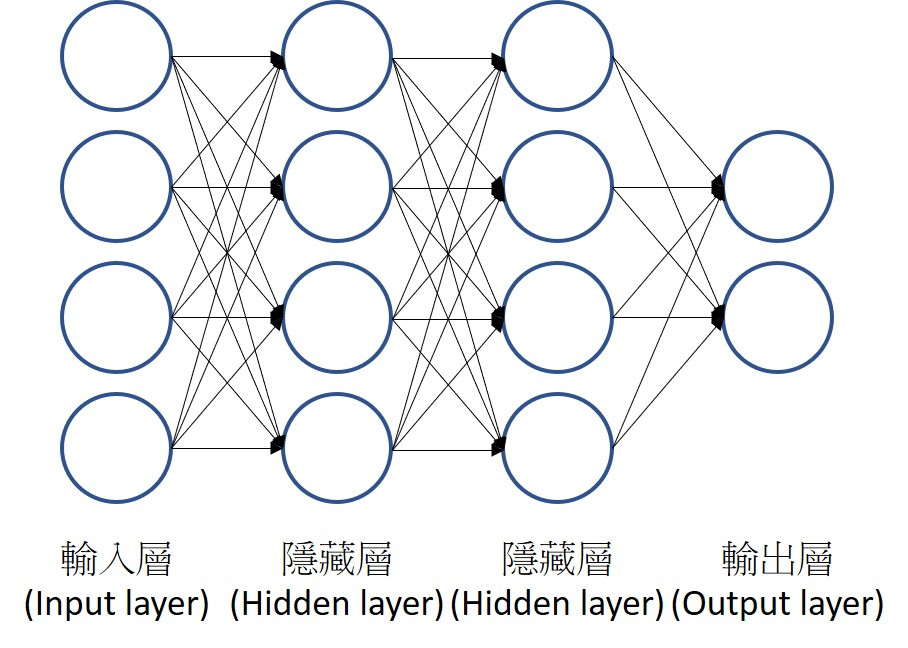

梯度下降法 (Gradient descent)

神經網路使用梯度下降法求得最佳解，將使用偏微分求得更新後的權重值，每次更新的幅度將依據學習率 (Learning rate)決定，當學習率設太大時，可能找不到最佳解，設太小時，將花費更多時間求解。以下為權種值更新的公式:

激活函數

深度學習裡常見的激活函數有sigmoid, relu等。如果隱藏層只有一層且激活函數為sigmoid，那這個模型等於羅吉斯迴歸 (Logistic regression)。Relu函數將小於0的值都輸出0，如果x大於0即輸出x，早期較常使用sigmoid函數，近幾年使用relu的準確率較高，因此皆使用relu當作激活函數。以下圖片來源為維基百科。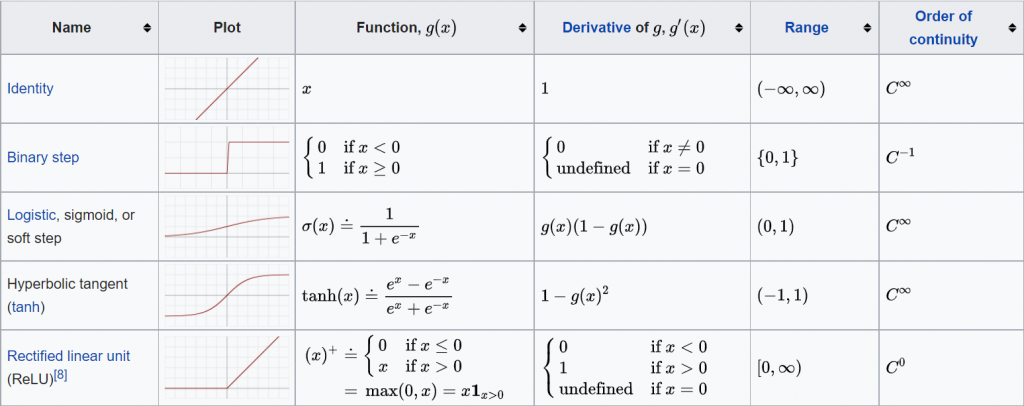

程式碼

梯度下降法

範例以f(x)=x^2實作梯度下降法，f’(x) = 2x。xs為儲存每次更新後的權重。

import numpy as np
import matplotlib.pyplot as plt

def func(x): return x ** 2

def dfunc(x): return 2*x

def GD(start, df, epochs, lr):
    xs = np.zeros(epochs+1)
    x = start
    xs[0]=x
    for i in range(epochs):
        x += - lr*df(x)
        xs[i+1] = x
    return xs

梯度下降法需先給定一個起始點，它並不是從0開始，如何挑選起始點也是一門學問。更新次數以及學習率也是需要預先給定的。

start = 5
epochs = 15
lr = 0.3
w = GD(start, dfunc, epochs, lr)
print(np.around(w,2))

最後，視覺化梯度下降後的結果。

t = np.arange(-6,6,0.01)
plt.plot(t, func(t), c = 'b')
plt.plot(w, func(w), c = 'r', label = 'lr = {}'.format(lr))
plt.scatter(w, func(w), c = 'r')
plt.title('Gradient descent')
plt.xlabel('X')
plt.ylabel('loss function')
plt.show()

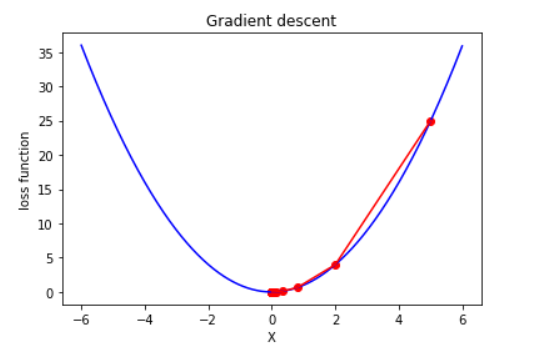
從圖我們可以看出，第一次更新權重時變化較多，第二次以後慢慢地變少。

程式碼已上傳github

最後，感謝您的瀏覽!