今日大綱

• 資料型態
• 敘述統計
• 機率分配
• 信賴區間

統計是從資料所得到的資訊，包含了敘述統計、機率分配等等。統計裡的專有名詞有觀察值 (observation)、資料集 (dataset)、特徵 (feature)或屬性 (attribute)與目標 (target)欄位等。以利用過去刷卡金額預測是否被盜刷為例，觀察值為每張新用卡的刷卡金額等其他屬性，資料集為所有蒐集到的信用卡，刷卡金額為特徵，目標欄位為是否被盜刷。

資料型態

1. 名目資料 (Nominal data)
   名目資料之間沒有次序的關係，例如性別，男女之間沒有次序之關係，在處理資料時會將男與女的文字轉成0與1，不代表任何意義。
2. 順序資料 (Ordinal data)
   順序資料之間存在次序性，有大小之分，例如衣服的尺寸XL、L、M與S，它們之間是有大小關係的。編碼之後的數字，並不能夠做加減運算。
3. 區間資料 (Interval data)
   區間資料並沒有絕對的零點，例如填答問卷時，所出現的非常滿意、滿意、普通、不滿意與非常不滿意等，能夠解釋非常滿意與滿意、滿意與普通這兩個之間的差距一樣大
4. 比例資料 (Ratio data)
   兩筆資料之間能夠做加減乘除之運算，例如身高、體重等。

敘述統計

將資料輸入製模型前，都會看看資料的分布，了解資料後進一步決定如何處理資料。主要分為兩種，第一種有關集中趨勢的指標，另一種為與資料的離散程度有關。

集中趨勢

1. 平均數 (Average):所有的資料相加並平均。
   
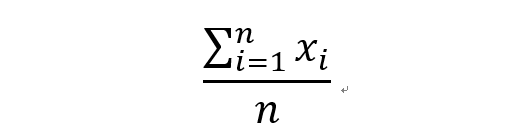
   平均數有個缺點，它容易受離群值 (Outlier) 影響，假設今天的資料點為[100,200,300,400,500]平均數為300，如果將500改成5000，那平均數將提高為10200。
2. 中位數 (Median): 將所有資料由大排到小，中間的資料點即為中位數。如果總樣本數為偶數，那將中間那兩個數值取平均即為中位數。
3. 眾數 (Mode): 出現次數最多的即為眾數，主要使用在離散資料上。

資料離散程度

1. 最大值
2. 最小值
3. 全距 (Range): 最大值與最小值之間的差距
4. 四分位距 (InterQuartile Range): 假設有n筆資料，將資料由小到大排序後，第n乘75%筆資料為第三四分位數 (Q3)，第n乘25%筆資料為第一四分位數 (Q1)，第三四分位數減去第一四分位數即為四分位距。
5. 變異數 (Variance): 當變異數越大，代表資料越分散。
   

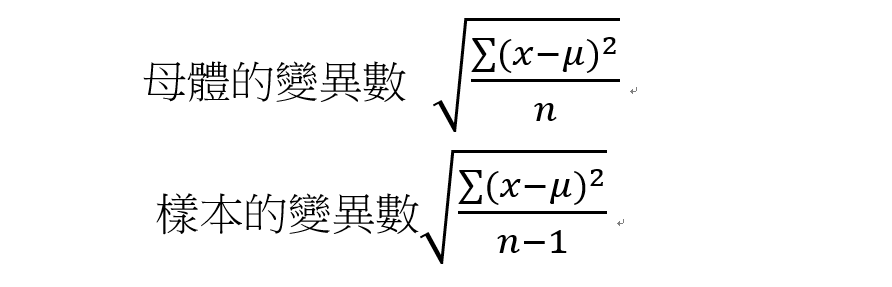
機率分配

首先，介紹幾個常見的專有名詞:

• 機率密度函數 (Probability density function, pdf): 發生各種事件的機率。
• 機率質量函數 (Probability mass function, pmf):如果資料是離散型態的機率分配則稱為pmf。

常態分配 (Normal distribution)

常態分配又稱為高斯分配 (Gauss distribution)，因為提出的人其姓為Gauss。大部分的事件都假設為常態分配，例如考試的成績，考高分與低分的人較少，大部分的人考的分數落在中間。其機率密度函數為

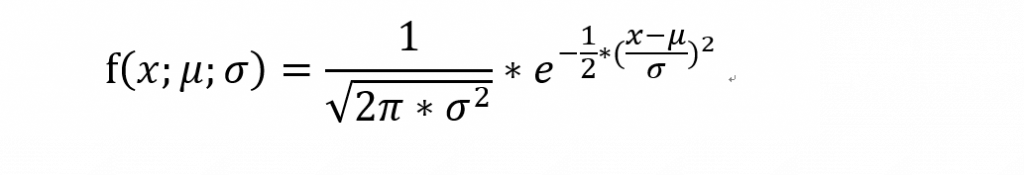
μ為平均數；σ為標準差。

均勻分配 (Uniform distribution)

此分布假設每個樣本發生的機率相同，例如擲骰子、擲硬幣，擲到每個面的機率都是一樣的。均勻分配的機率密度函數如下:

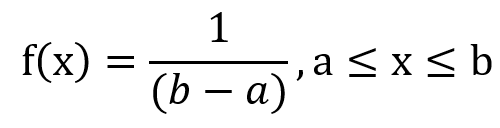
二項分配 (Binomial distribution)

二項分配的結果只有兩個，成功/失敗、正面/反面等。

1. 伯努利分配 (Bernoulli distribution): 做一次二分類的實驗，機率密度函數如下:
   

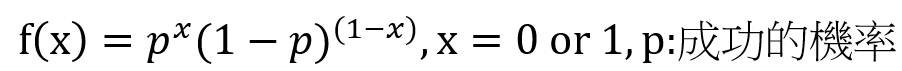
2. 二項分配 (Binomial distribution): 做多次二分類的實驗，機率密度函數如下:
   

卜瓦松分配 (Poisson distribution)

卜瓦松分配主要是計算在某段時間內某事件發生的次數，例如在早上10點到12點來客數幾個人，用來估計等候人數，進一步推估需要幾個服務人員。其機率密度函數如下:

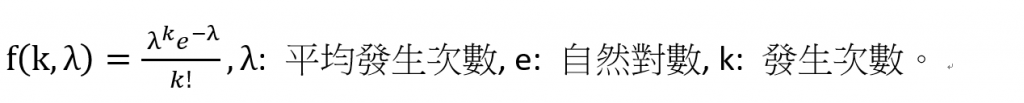
信賴區間 (Confidence level)

最後，介紹甚麼是信賴區間。在做假設檢定時，常常會使用到信賴區間。在常態分配裡，隨機給定一個資料點，有68%的信心水準能說資料落在距離平均數一個標準差的範圍內；95%的信心水準這個資料在兩個標準差之內；99.7%的信心水準說這個資料落在三個標準差內。

今天的介紹到此為止，感謝您的瀏覽
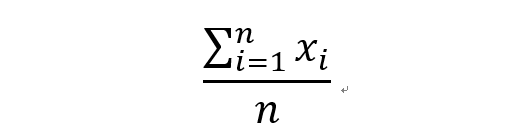
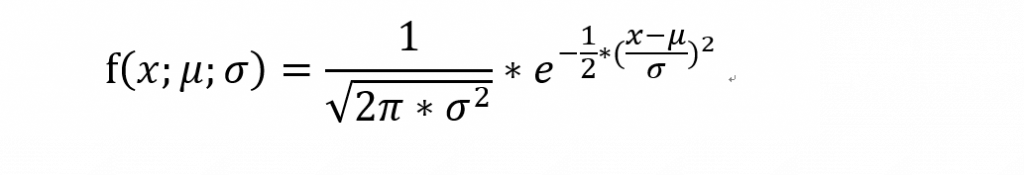
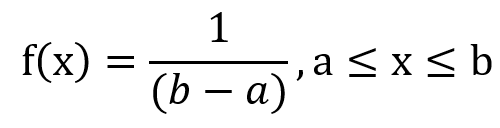
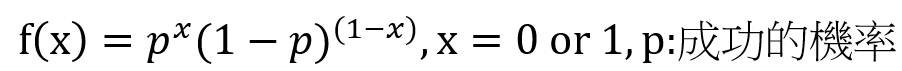
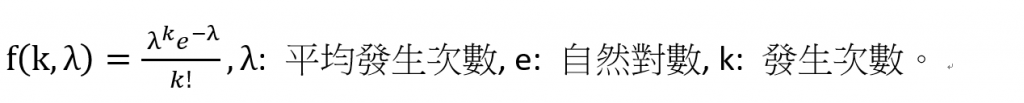