今天要探討的是我在**[Day13] 多元線性回歸(05) - Example** 中的問題延伸
還記得這個例子我用的是Backward Elimination 方法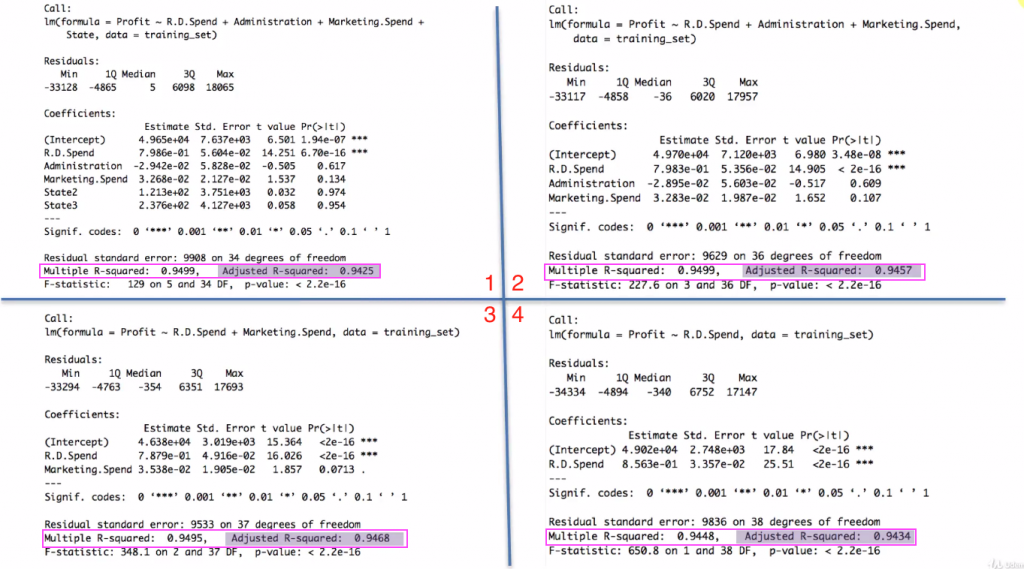

圖片中顯示的是擬合完的結果
1,2,3,4分別是每一次踢除一個變數後的結果

1→2: 去掉state
2→3: 去掉administration
3→4: 去掉Marketing Spend
因為我們設定 P-Value(threshold) 為5%
雖然 Marketing Spend這項變數的P-Value 只大於5%一些
但因為threshold的緣故, 所以還是會被剔除
最後第四張圖只留下 RD Spend 一個變數當作最終擬合的變數選擇

可以想見這樣的方式下, 選擇threashold 變得很重要
如果改為選擇8% 那 Marketing Spend 就會被留下來
因此需要一個更客觀的方法來評價模型的好壞, 而不是用主觀定義的門檻

接著我們回憶一下昨天講到的Ｒ平方概念
當新增一個變數到模型中, New R平方會 ≥ Original R平方
從這個例子中可以驗證這個概念
我們從4往前看
4→3 新增一個變數, 所以R平方從 0.9448 → 0.9495 (變大）
3→2 新增一個變數, 所以R平方從 0.9495 → 0.9499 (變大）
2→1 新增一個變數, 所以R平方從 0.9499 → 0.9499 (沒有變, 代表 State 對結果的解釋度最低, 不具影響力)

前面我們說過如果單用Ｒ平方來評斷一個模型的好壞是不夠的
以2→1 來說, 1 的Ｒ平方達到最高, 理論上越高代表模型擬合度越好
但state 其實跟profit 沒有太大的關係(因為R平方從2→1沒有變), 所以單看Ｒ平方是不夠的
所以我們引入廣義Ｒ平方的概念

廣義Ｒ平方 = 1 - (1-R^2) * (n-1)/(n-p-1)
廣義Ｒ平方越大, 代表模型越好
為了方便說明, 我將：
(1-R^2) 定義為 A
(n-1)/(n-p-1) 定義為 B
自變量(p)個數越多, 某種程度上來說, 會懲罰“廣義Ｒ平方”的結果, 因為p變大, B上升
但是自變量個數越多, 也會讓Ｒ平方上升, A 變小
因此Ａ, B 一升一降會交互影響
若Ｂ的影響比較多, 會讓廣義Ｒ平方變小
若Ａ的影響比較多, 會讓廣義Ｒ平方變大
所以可以更公正的來評價模型的好壞

看圖2→1 廣義Ｒ平方從 0.9457 → 0.9425(變小)
代表變數的增加讓Ｂ上升, 也讓Ａ下降
但是上升的影響比較多, 所以整體“廣義Ｒ平方”下降
所以2號模型其實是比較好的

3→2 廣義Ｒ平方從0.9468→0.9457 (變小)→ 代表3其實比較好
4→3 廣義Ｒ平方從0.9434→0.9468(變大) → 代表3還是比較好
所以最終我們發現用廣義Ｒ平方是可以得到一個比較好的選擇
也就是保留 RD Spend, Marketing Spend 兩個變數

那反向淘汰還需要嗎？ 答案是要！
因為我們可以從第一步開始, 有順序的刪除自變量
並在過程中觀察Ｒ平方與廣義Ｒ平方來得到最好的結果