今天要來繼續探討多元線性回歸參數的意義
我們一樣用上一篇的例子來說明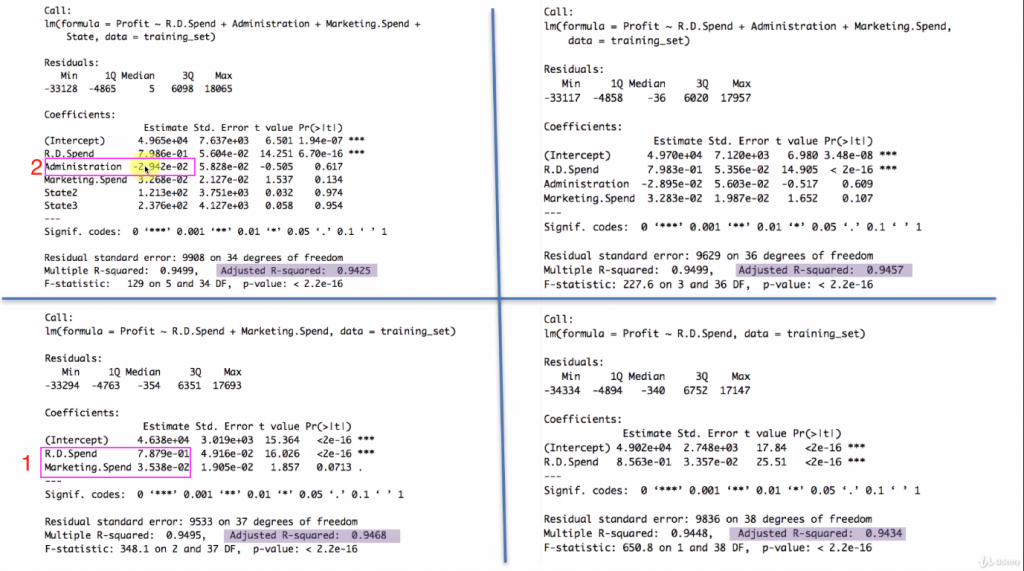

下面我們只針對 Estimate 來討論

參數符號的意義

參數的正負

當參數是正數, 代表自變量越大, 最終應變量也越大
當參數是負數, 代表自變量越小, 最終應變量也越小

紅框1) 可以看到RD Spend是正數, 因此RD Spend越多, 預測的公司profit 也越多
紅框2) Administration 是負的, 代表行政費用開支越多, 對profit 越差
代表公司必須要檢討行政費用的花費

參數的值

RD Spend = 0.7879
Marketing Spend = 0.03538
RD Spend 顯然遠大於Marketing Spend

Ｑ：這代表RD Spend 對 profit 的影響遠大於Marketing Spend？
以這個範例是yes, 原因是本範例中的自變量單位都是1美元
所以可以相互比較
參數代表的涵意與自變量的單位息息相關
一般來說, 自變量的單位很可能都不同(ex: m, cm or k, g) 因此很難把這些不同單位的自變量放在一起比較
例如 x=50, y=10 乍看之下 50>10 但x的單位其實cm, y的單位是m
因此其實 x = 50cm, y = 1000cm, 所以 x < y 才對
不過單位不同的情況下, 雖然不能把自變量之間的絕對關係做比較
卻可以把單一變量跟結果做比較:
** " 在單位自變量的變化下, 應變量也有相對應的變化"**
上面例子就可以解讀成：
假設RD Spend 增長了一個單位, 那麼profit 就會相應增長0.7879個單位

再回到本範例中的自變量單位都是1美元所以可以相互比較的結論下
我們可以得到： RDSpend 的係數大約是Ｍarketing Spend 係數的20倍

因此對投資人來說
每花1美元到RDSpend 對profit 的影響相當於投入花20美元到Ｍarketing Spend對profit 的影響

所以這個結論對投資者來說是有意義的
顯然投入到RDSpend 對profit 的影響會比投入到Ｍarketing Spend 更大

不同模型中同一個自變量的觀察

對於同一個自變量, 例如 RDSpend, 在不同的模型中數值都不同
雖然說係數間的差別不大, 但仍代表這一個自變量跟其他自變量的存在與否有關係
因為一個係數代表著在此模型下, 其他自變量都不變的情況下
只對這一個自變量做出改變時, 對結果所帶來的影響

以上就是透過實際例子來說明機器學習能為數據帶來更多效益的地方