今天進入到 GAN 的理論了，真是讓人既期待又害怕受傷害（？

在這裡為了簡化說明，所以都是以 unconditional GAN 為例子～

視覺化的解釋

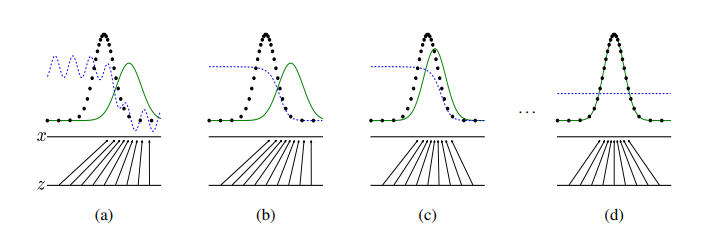
下圖是 GAN paper 提供的一個簡化的示意圖，從這張圖我們可以先直觀的了解 generator 和 discriminator 之間的互動，以及 generator 怎麼從真實影像分布學習出相似的生成分布：

（圖片來源：Generative Adversarial Networks）

圖中的黑點指的是我們從真實影像的分布抽樣出來的樣本，假如有充分且均勻的抽樣，這些樣本可以大略的代表真實的分布。而訓練 GAN 就是希望 generator 學習到真實的分布，圖中綠色曲線是 generator 學到的分布，訓練的最終目標是讓綠色曲線和黑點越重合越好，z 到 x 的箭頭則是表示 generator 將輸入分布 z （可能是常態分布）投射到輸出的影像分布 x。至於藍色曲線則代表 discriminator 的分布，discriminator 學習的目標是，如果影像來自真實資料（黑點），就給它高分；如果來自生成分布（綠線），就給它低分。因此，一開始當生成分布（綠線）和真實資料（黑點）重合很少時，discriminator 可以判別得很好（如圖 b）。

在重複訓練 discriminator 和 generator 多次後，generator 學到的分布（綠線）會逐漸和真實資料分布（黑點）變得接近，discriminator 會越來越難以判別，但是在生成分布（綠線）和真實資料（黑點）還沒完全重合前，discriminator 還是可以區分出一些真實影像和生成影像的差異，並引導 generator 學習（如圖 c）。

訓練到最後，理想上 generator 學到的分布（綠線）會和真實資料分布（黑點）完全重合，這時 discriminator 也完全分辨不出真實影像和生成影像的差異（藍色曲線變成平的，不會有哪些地方比較高分或比較低分），GAN 就訓練完成。

演算法

（圖片來源：Generative Adversarial Networks）

如上圖，GAN paper 中有蠻清楚的寫到整個演算法與目標函數的數學形式。

如同先前在「如何訓練 GAN？」提到的，我們會重複訓練兩個步驟：

1. 給定 generator，訓練 discriminator
2. 給定 discriminator，訓練 generator

在訓練 discriminator 時，首先要在輸入分布抽樣好幾筆隨機向量 {z_1, z_2, ..., z_m}，通過 generator 後得到幾張生成影像，如果用 G 代表 generator，任意的生成影像可以表示為 G(z_i)。另外，我們也需要從真實資料分布 p_data 抽樣幾張影像 {x_1, x_2, ..., x_m}。

接著的數學式，代表的是 discriminator（D）的目標函數的 gradient，discriminator 學習的方向是讓目標函數越大越好，而 gradient 則可以看成每個參數的變動對目標函數的影響，為了最大化目標函數，discriminator 的參數必須依照梯度變大的方向更新。

至於這個 discriminator 的目標函數，乍看可能不明所以，其實它就是 discriminator 輸出影像真實程度的 log likelihood，換句話說，我們其實就是把 discriminator 當成一個二元分類器，專門把影像分成真實的和生成的，它和訓練其他二元分類器的方式是沒有差別的。

而在訓練 generator 時，我們只需要準備一些 generator 產生出來的影像 G(z_i)，通過 discriminator。它的目標函數基本上就是 discriminator 的目標函數只取跟生成影像有關的部分，但不同於訓練 discriminator 的是，我們必須訓練 generator 讓這個目標函數越小越好。換句話說，原本在訓練 discriminator 的時候，我們希望 discriminator 給生成影像的分數越接近 0 越好，但在訓練 generator 的時候，因為希望產生出來的影像是能「騙過」discriminator 的，因此期望更新 generator 的參數，讓 discriminator 的輸出分數越接近 1 越好。

在原作 paper中，作者也證明了，在 generator 和 discriminator 都有足夠的學習能力（capacity）的情況下，GAN 的機制能讓 generator 學到的分布 p_g 會收斂到真實影像資料的分布 p_data。至於要怎麼證明呢？詳情請參考 paper（就不班門弄斧了

然而在實際訓練模型時，由於模型參數是有限的，參數數值的精度也是有限制的，得到的生成模型和理論結果勢必有落差。事實上，訓練出一個好的 GAN 是不太容易的。如果有興趣自己訓練看看，應該就會對於這種理論與實務間的差距很有感觸呢！

以上內容主要是參照原始版本的 GAN paper 整理出來的理論脈絡，這裡略過了理論證明的部分，不然...相信讀者和我都會很痛苦吧

另外，李宏毅老師的機器學習課程對於 GAN 的理論也提供了另一個角度的解釋。

由於我們希望 generator 能學習到真實影像的分布，那怎麼評估 generator 學到的分布和真實影像分布是否接近呢？Divergence 就是一種評估兩個分布接近程度的指標。Divergence 其實有很多種類（例如 JS divergence、KL divergence），但要計算 divergence 最大的問題是，我們實際上並不知道分布的數學表示啊

對此，GAN 用了很巧妙的方式解決了這個問題：假設我們能夠均勻且充分的抽樣出真實資料樣本和生成資料樣本，就能夠推估真實影像分布和生成分布的 divergence。

至於如何推估呢？當我們使用一個二元分類器當作 discriminator，discriminator 越能區分出真實影像和生成影像，就代表分布間的 divergence 越大（真實影像分布和生成分布差很多）；反之，如果 discriminator 難以判別真實影像和生成影像，代表分布間的 divergence 是小的（真實影像分布和生成分布相近）。在原始 GAN paper 中，作者也有推導出 discriminator 的目標函數確實和 JS divergence 相關。

關於 GAN 理論的簡介，今天就告一段落，希望大家還沒昏頭啊啊啊