[Day14]：WGAN原理介紹

前言

昨天介紹了DCGAN的實作，在DCGAN的實作中個人經驗是相當容易出現梯度消失等問題。在解決訓練不平衡與梯度消失等問題時也會常常使用Wasserstein GAN (WGAN)，使用WGAN可以比較好的增進訓練的平衡性。接下來就來看看WGAN背後的祕密吧。

WGAN是甚麼？

WGAN，全稱是 Wasserstein GAN，他是一種生成對抗網路的變體，主要是目標函數與傳統的不同，WGAN它最小化的是Earth-Mover (EM)距離的近似，而不是原始GAN中的Jensen-Shannon (JS)散度。它有以下幾個優點：

• 它可以提供有意義的學習曲線，不像普通的GAN訓練的損失看不太出來訓練成果，只能大致看出訓練有沒有失衡。這個目標函數也可以用於調整超參數等。
• 它可以很好的避免模式崩潰 (Mode Collapse)的問題，即生成器只能生成幾種固定的樣本。
• 它可以提高學習的穩定性，不需要精心設計的網路架構和激活函數，例如昨天的DCGAN就花了一些時間去調整模型架構與超參數的選擇等。

WGAN的主要改進是使用判別器，該判別器會用來近似EM距離，而不是單純只是一個判斷器來判斷圖片真假，並且對判別器的權重進行裁剪(Clipping)，使其符合一個Lipschitz約束。

看了上段的文章，可能有很多名詞需要解釋，接下來就來解釋這些名詞的意思：

1. Kullback-Leibler (KL)散度：在介紹JS散度以前要先介紹KL散度。KL散度也是一個衡量資料分布相似度的計算方式，它可以用來表示用一個分佈來近似另一個分佈時，所造成的訊息損失。與JS散度不同的是KL散度並沒有對稱性，所以在計算P與Q的相似度跟Q與P的相似度可能會不同。

   KL散度的公式如下，其中第一個公式計算的是P與Q的分布相似度，P與Q就是兩個機率分布。值得注意的是上面的公式與下面的公式計算出來的值可能會不同喔。

   

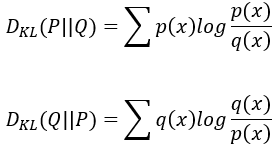
   KL散度GAN中很重要的概念，但因為其理論較複雜，對機率分布與微積分有一點要求。故在此舉個簡單的例子：假設今天在玩抽卡遊戲，遊戲中有兩個卡池P與Q (P池與Q池都有N、R、SR、SSR卡，且兩個卡池中各等級的卡假設抽到機率不同)。今天我們已P池為基準，從Q池中抽卡，看看這張卡是甚麼，如果這張卡在P池很多 (例如N卡)，那這次抽卡就沒有驚喜感；相反的抽到SSR就會又驚又喜。今天來個100連抽，把每一次抽取的驚喜感加起來就得到了用P池來近似Q池所需要的訊息量。如果這個信息量很小代表P與Q池的分布類似，反之亦然。

2. Jensen-Shannon (JS)散度：各位可能會覺得很奇怪，JS散度是甚麼，為何突然說是GAN中要嘗試最小化的函數。JS散度是一種衡量兩個資料分佈之間相似度的方法，是KL散度的變體，它可以反映分佈之間的相似度，越小表示越相似，越大表示越不相似，這與原始GAN中的目標函數就是相似的東西。

   JS散度的公式推導如下，為了解決對稱性的問題，我們假設了一個機率分布M。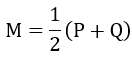
   

   接著把M與KL散度結合變成這樣，可以當成JS散度是計算P和M與Q和M分布相似度的算術平均：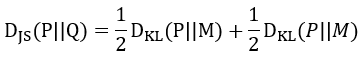
   

   接著將KL散度展開並化簡，可以得到最終成果，這個結果就具有對稱性：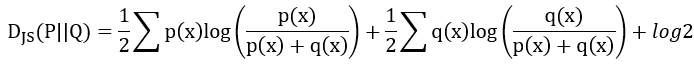
   

   不過JS散度有一個缺點就是當兩個資料分布完全不重疊時，無論兩個分布中心有多近，JS散度都是log2，導致他的梯度為0，也就是會梯度消失。

   JS散度也舉個簡單的例子：今天一樣是P與Q池，但遊戲的工程師M將P與Q池混和接著平均成兩份，推出了P1池與Q1池。這樣做的目的是讓兩個新卡池裡面卡的稀有度分布都接近於原來兩個舊卡池裡面卡的稀有度分布的平均值。然後你分別計算用卡池P1來近似卡池P和用卡池Q1來近似卡池Q所需要的訊息量，並且取它們的平均值。這個平均值就是JS散度。它也可以反映兩個舊卡池裡面卡的稀有度分布的相似程度，而且不會受到基準選擇的影響。

3. Earth-Mover (EM)距離：EM距離是一種衡量兩個資料分佈之間差異的度量方式，也叫做Wasserstein距離，WGAN就是主要使用這個衡量方式。它可以理解為將一個分佈轉換為另一個分佈所需要的最小工作量。例如今天有兩坨完全不一樣的黏土，將其中一個黏土轉換成另一個黏土使兩個黏土完全一樣，所作出的最小工作量就是Wasserstein距離。
   根據原始論文中的方程式1.，我們可以看到EM距離公式如下：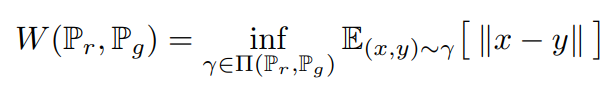
   
   哇！出現了一堆各位可能沒看過的東東，沒關係，我們一個一個看~

   • inf是取下界的意思，他的定義是小於等於在集合中所有數的最大實數。
   • γ代表他屬於(∈) Pr 跟 Pg 組合起來的所有聯合分布的集合( Π(Pr,Pg) )。拿剛剛的黏土來舉例，就是將 Pr 黏土變成 Pg 黏土的所有方式。例如一個正方體黏土要變成長方形黏土，你可以將正方體搓長再捏成長方體；或者將正方體切小塊再合成長方體等等，這些方法的集合就是γ。
   • 後面那個東東 (x,y)~γ 可以看做是從這些方法中採樣其中一種，接著要計算那個方法的期望。計算方式很簡單，就是計算兩個分布中的差並取絕對值，然後加起來就好了。

   所以全部看下來，EM距離就是在計算把一個分布 Pr 變成另一個分布 Pg ，這些變化方法中有許多聯合分布，這些聯合分布裡面能夠使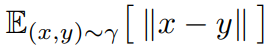最小的那個期望值就是所要求的。

4. Lipschitz約束：Lipschitz約束是一種限制函數變化速度的條件，它要求函數必須有一個最大的梯度。具體的最大梯度是一個超參數，可以自己設定。Lipschitz約束的作用是保證如果兩個輸入圖像相似，那麼函數的輸出也相似。Lipschitz約束能夠使得生成器和判別器之間的平衡更加穩定。

與GAN有甚麼不同？

WGAN與GAN的不同主要有以下幾點：

• WGAN使用EM距離來衡量真實分佈和生成資料分布之間的差異，而GAN使用JS散度。EM距離可以更好地反映資料分布之間的相似度，而JS散度在分佈不重疊時會出現飽和問題。

• WGAN的鑑別器不再是一個判斷圖片真假的判別器，而更可以說是一個衡量圖片品質的評價器，它輸出的是一個數值，表示圖片屬於真實分佈的程度 ，而不是機率。這樣可以避免使用對數函數和Sigmoid函數，減少梯度消失的風險。判別器會計算生成圖片屬於真實分佈的程度與真實圖片屬於真實分佈的程度，這兩個差異就是EM距離。判別器一樣要最大化這個距離，生成器要最小化這個距離。

  也就是說WGAN的鑑別器不是說圖片是真是假，而是有多像真的。

• WGAN對判別器的權重進行裁剪，使其符合一個Lipschitz約束，並加以保證EM距離的有效性。這樣可以避免生成器模式崩潰。

• WGAN的學習曲線可以反映出生成圖片質量的變化，而GAN的學習曲線往往沒有太重大的意義，也無法看出圖片生成的質量為何。使用WGAN就可以更方便的調整模型。

講了那麼多優點，WGAN有沒有缺點，那是當然有的，例如：

• 訓練速度比較慢，因為在計算EM距離以及對權重進行裁剪都會耗費一些計算資源。
• 使用權重裁剪有可能導致權重集中在裁剪的極值。

結語

今天向各位介紹了WGAN的一些基礎知識，希望各位能夠理解這些內容，當初我也是看了非常久才懂了其運作原理。不過無法完全理解沒關係，這些內容寫成程式卻意外的簡單，明天就會帶各位實作WGAN，各位實作WGAN時也可以看看與之前的GAN相比訓練上有沒有差異。

當初的我be likes (在未來看到擴散模型的數學原理可能也是這種情況XD)：