接下來要介紹的是 flow-based model 的數學原理，今天首先會需要介紹到相關的數學概念與定理

關於 flow-based model 的原理，我也還正在理解中，如果有解釋得不對的地方，請不吝指正

相關的數學概念

由於接下來要介紹的 flow-based model 的原理會使用到幾個線性代數或微積分的概念，所以在此會先簡介一下～但如果本來就不熟悉線性代數和微積分的話，這一段可能會有點辛苦，可以先記得它們代表的意義就好（這些東西我也快忘光啦

Jacobian matrix

當有一個函數 f(x) 會將輸入的 x 向量投射到另外一個空間的向量，這個函數對 x 的所有偏微分組成的矩陣，就是 Jacobian matrix，它的形式如下：

而 Jacobian matrix 常被用於座標轉換。

Determinant

Determinant 是一個純量，每個方形的矩陣（行和列數相等的矩陣）可以特定計算方法得出，我們可以透過 determinant 掌握一些矩陣的性質，例如矩陣是否可逆，以及矩陣變換對體積的影響。

一個矩陣 A 的 determinant 會被記作 det A，而計算方式會是方形矩陣的元素依照特定規則計算乘積再加總起來，對於 2x2、3x3 的矩陣來說，非常容易取得 determinant 的計算公式，不過如果是高維的矩陣，可能就需要使用拉普拉斯展開（Laplace expansion）計算。

由於在理解 flow-based model 原理時，不一定要知道 determinant 的計算方式，因此這裡就略過。

除此之外，determinant 可以看作向量在空間中展開的「體積」，這個概念對於生成模型將 code 空間的分布投射到影像空間分布很重要。

Change of Variable Theorem（變數變換定理）

Change of Variable Theorem 是微積分中的一個重要定理，它提供了一種方法，用於計算積分中的變數變換後的積分，能用來簡化並處理複雜的積分。

首先直接套用生成任務的例子，但先以一維積分為例。假設影像的分布為 p(x)，code 的分布為 π(z)，由於機率分布的積分都為 1，因此可以寫下以下的等式：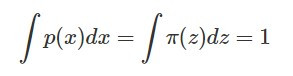

整理之後得到下式：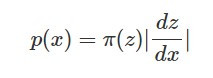

我們可以透過一個 generator G(z) 將 z 轉換為 x，因此 x = G(z)，而根據 flow-based model 的要求，G(z) 必須是可逆的，因此將影像投影到 code 的 encoder 就是 G(z) 的反函數 G^-1(x)，將 z = G^-1(x) 帶入上式就可以得到：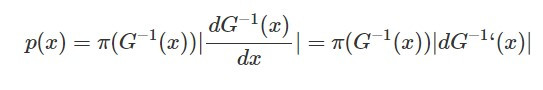

推廣到高維的情況則是如下列的形式：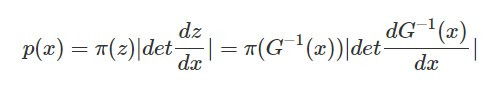

這就是在只使用一個 generator 的情況下，我們可以怎麼找到影像分布 p(x)～然而 flow-based model 是由一系列的 generator 所構成，明天將會討論這部分的數學

參考資料

• Flow-based Generative Model
• Flow-based Deep Generative Models | Lilian Weng