今天來說說第一個 QSVT 的應用：QPE。還記得剛開始的前幾天，我們認識了三種 QPE 演算法嗎？介紹完 QSVT 之後，我們將迎來第四種 QPE 演算法！

令 為我們感興趣的 unitary matrix，且 是我們想測量的 phase。考慮矩陣 ，其含有一奇異值 ：

假設 可以由 位元表示，即 ，則 含有一奇異值 ：

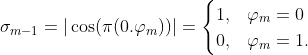
於是， 的資訊可以如下獲得：

其中

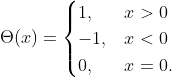
接著進行類似於 Itetative QPE 的步驟：透過先前的測量結果來作為之後量子電路的輸入，逐一計算出 的每個位元。請容我不贅述細節了！(像是為什麼有 ；詳見這) 直接附上電路圖供大家參考：(圖來源：A Grand Unification of Quantum Algorithms, p.18, Fig 11)

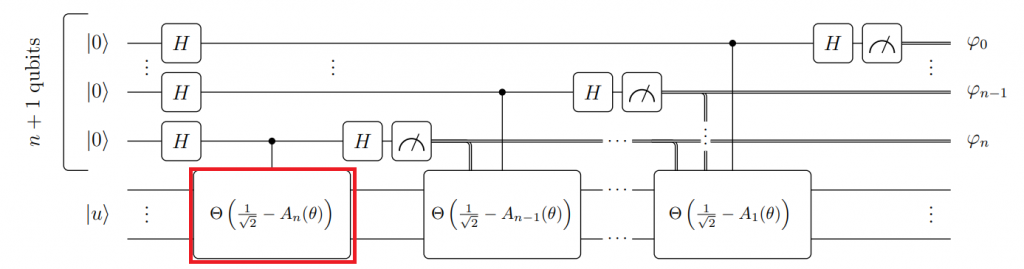
簡而言之，利用 QSVT 的 QPE 演算法可以總結成以下步驟：

1. 利用多項式 逼近 ，並找出相應的角度序列
2. 將 透過 QSVT 作用在 的奇異值上
3. 用類似 Iterative QPE 的方法，逐一測量出 phase 的每一位元，並將測量結果回饋到之後的電路

根據筆者粗淺的理解，利用 QSVT 的 QPE 雖然有減小估計錯誤的優勢 (詳見這)，但是電路深度卻大大的提高：紅框標示處並非單一量子閘，而是深度與 的 degree 成正比的子電路！即使這樣的演算法實現可能性低，它依舊展現了 QSVT 眾多可能性之一！明天我們將迎接 QSVT 的另一種應用！

參考資料

• A Grand Unification of Quantum Algorithms