本文同步更新於個人網站中，有更好的排版和程式碼區塊 highlighting 支援。

樹的走訪（traversal）或者說遍歷是一個很基礎的問題，有很多實際應用，可以用來找到匹配的字串、檔案路徑等問題。樹的走訪有兩種方式：深度優先（Depth First Search）和廣度優先（Breadth First Search）。

深度優先走訪又根據處理某個子樹的根節點順序不同，可以分為：前序（Preorder）、中序（Inorder）、後序（Postorder）。

• 前序走訪（Preorder）：先處理最上面的根節點，然後第二步是左子樹，最後是右子樹。
• 中序走訪（Inorder）：將最上面的根節點留到第二步，第一步為左子樹，第三步為右子樹。
• 後序走訪（Postorder）：根節點留到最後一步處理，第一步是左子樹，第二步是右子樹。

深度優先走訪的遞迴實作

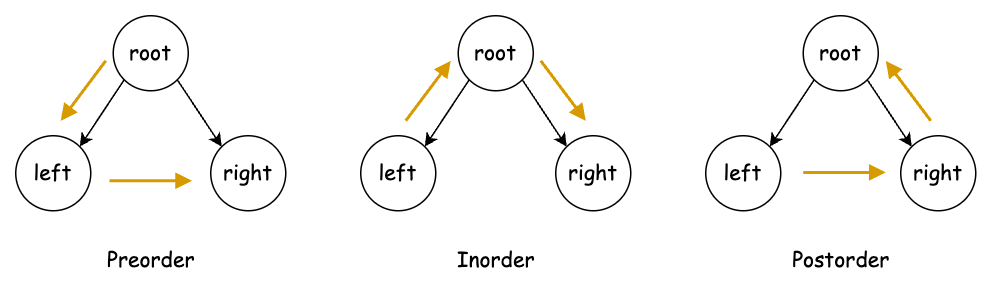
從上面的流程描述來看，深度優先走訪很適合用遞迴來實現。我們透過下面的程式碼來實作前序、中序、後序這三種走訪方式，然後借助 type 去選擇走訪方式：

inOrder(callback) {
  this._forEach(this.root, callback, 'middle');
}

preOrder(callback) {
  this._forEach(this.root, callback, 'pre');
}

postOrder(callback) {
  this._forEach(this.root, callback, 'post');
}

_forEach(node, callback, type) {
  if (node) {
    if (type === 'middle') {
      this._forEach(node.left, callback, type);
      callback(node);
      this._forEach(node.right, callback, type);
    } else if (type === 'pre') {
      callback(node);
      this._forEach(node.left, callback, type);
      this._forEach(node.right, callback, type);
    } else if (type === 'post') {
      this._forEach(node.left, callback, type);
      this._forEach(node.right, callback, type);
      callback(node);
    }
  }
}

我們在總結一下這三種走訪的輸出結果有什麼特點：

• 前序：陣列的第一個元素是根節點。(ABDECFG)
• 中序：根據根節點劃分了左右子樹的元素。(DBEAFCG)
• 後序：陣列的最後一個元素是根節點。(DEBFGCA)

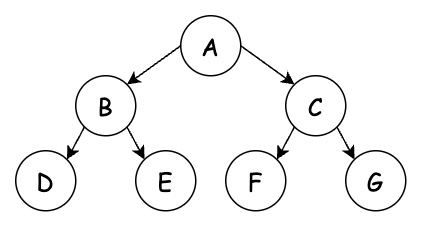
現在來透過一道題目來驗收一下學習成果：

已知二元樹的中序和前序走訪結果，如何求後序走訪結果？例如一棵樹的前序走訪是“GDAFEMHZ”，而中序走訪是“ADEFGHMZ”，應該如何求其後序走訪結果？

具體步驟如下：

1. root 最簡單，前序走訪的第一個節點 G 就是 root。
2. 看中序走訪，ADEF 在 G 的左邊，HMZ 在右邊。

3. 觀察左子樹 ADEF，左子樹中的根節點必然會是大樹 root 的 leftChild。在前序走訪中，大樹 root 的 leftChild 位於 root 之後，所以左子樹的根節點為 D。

4. 同樣的道理，root 的右子樹節點中的 HMZ 中的根節點也可以透過前序走訪找到。在前序走訪中，一定會把 root 和 root 的所有左子樹節點都遍歷完之後才會遍歷右子樹，並且遍歷右子樹的第一個節點就是右子樹的根節點。
   如何知道哪裡是前序走訪中左子樹和右子樹的分界點？透過中序走訪去數節點的個數。
   中序走訪中，root 左側是 ADEF，所以有 4 個節點位於 root 左側。那麼在前序走訪中，第一個是 G，2~5 個由 ADEF 組成，所以第 6 個節點就是右子樹的根節點，也就是 M。

5. 觀察上述步驟發現，所有過程都是遞迴的。先找到目前樹的根節點，然後劃分左子樹、右子樹，然後進入左子樹重複上面過程，再進入右子樹重複上面過程。最後就可以還原出整棵樹的結構。

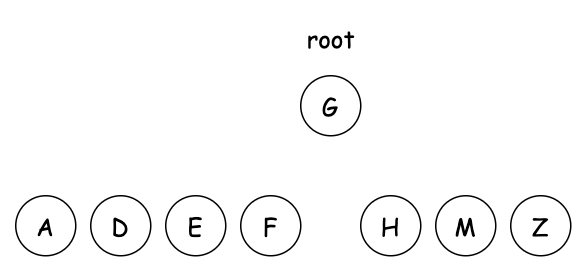
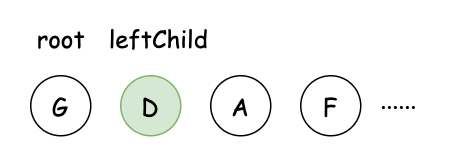
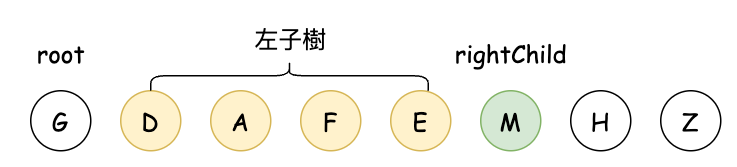
其實如果只是要求寫出後序走訪，甚至不要求專門佔用空間保存還原後的樹。只需要稍微改動第 5 步，就能實現要求。僅需把遞迴過程改成：

1. 確定根，確定左子樹，確定右子樹。
2. 在左子樹中遞迴。
3. 在右子樹中遞迴。
4. 處理目前的根節點。

用程式表達的話如下：

function getPostorder(preorder, inorder, postorder = []) {
  const root = preorder[0];
  const inLeftTree = [];
  const inRightTree = [];
  let list = inLeftTree;

  // 分離出 inorder 的左右子樹
  for (let i = 0; i < inorder.length; i++) {
    if (inorder[i] === root) {
      list = inRightTree;
    } else {
      list.push(inorder[i]); // 根節點不會放在兩個子樹中
    }
  }

  const boundary = inLeftTree.length;
  const preLeftTree = [];
  const preRightTree = [];

  // 分離出 preorder 的左右子樹
  for (let i = 1; i < preorder.length; i++) {
    const el = preorder[i];
    if (preLeftTree.length < boundary) {
      preLeftTree.push(el);
    } else {
      preRightTree.push(el);
    }
  }

  // postorder 左子樹遞迴
  if (preLeftTree.length > 0) {
    getPostorder(preLeftTree, inLeftTree, postorder);
  }

  // postorder 右子樹遞迴
  if (preRightTree.length > 0) {
    getPostorder(preRightTree, inRightTree, postorder);
  }

  // postorder 處理根節點
  if (root) {
    postorder.push(root);
  }

  return postorder;
}

題目中的 Tree 結構還原後如下：

深度優先走訪的非遞迴實作

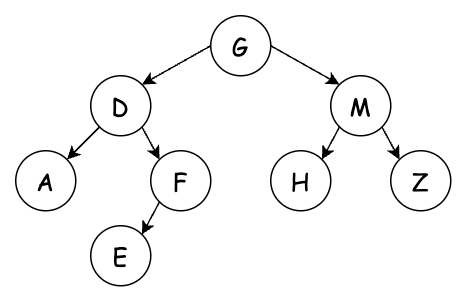
使用 stack 取代遞迴，首先要用一個 while 迴圈將所有的節點都放入 stack 中，然後再一個一個取出來處理。先不放根節點，統一在迴圈內部去放。

xxxOrder(callback) {
  const stack = [];
  let node = this.root;
  while (node || stack.length) { // 將所有子節點推入 stack
    if (node) {
      stack.push(node);
    } else {
      node = stack.pop();
    }
  }
}

迴圈中有兩個分支，分別做 push 和 pop，push 的條件是 node 存在，以這個為界切開迴圈。前序和中序都是先 push left 再 push right，實作程式碼如下：

preOrder(callback) { // 口訣：中左右
  const stack = [];
  let node = this.root;
  while (node || stack.length) {
    if (node) {
      callback(node); // 中先於左
      stack.push(node);
      node = node.left; // push left
    } else {
      node = stack.pop();
      node = node.right; // push right
    }
  }
}

inOrder(callback) { // 口訣：左中右
  const stack = [];
  let node = this.root;
  while (node || stack.length) {
    if (node) {
      stack.push(node);
      node = node.left; // push left
    } else {
      node = stack.pop();
      callback(node); // 中先於右
      node = node.right; // push right
    }
  }
}

postOrder(callback) { // 口訣：左右中
  const stack = [];
  const out = [];
  let node = this.root;
  while (node || stack.length) {
    if (node) { // 類似於 preOrder，可以當作 根 -> 右 -> 左，然後再反轉
      stack.push(node);
      out.push(node);
      node = node.right;
    } else {
      node = stack.pop();
      node = node.left;
    }
  }
  while (out.length) {
    callback(out.pop());
  }
}

練習：一棵二元搜尋樹，找出樹中第 k 大的節點。

二元搜尋樹後面會介紹到，總之就是一棵樹，每個節點的值都大於左子樹的所有節點的值，我們要從這棵樹中找出第 k 大的節點。我們這裡先關注如何透過中序走訪來解決這個問題。

方法一：最樸素的方法是透過中序走訪將二元樹轉換成陣列，然後取出索引值為 k-1 的元素即可。

function kthNode(root, k) {
  if (!root || k < 0) {
    return null;
  }

  const array = [];
  inOrder(root, array);
  if (k > array.length) {
    return null;
  }
  return array[k - 1];
}

function inOrder(root, array) {
  if (root === null) {
    return;
  }
  inOrder(root.left, array);
  array.push(root);
  inOrder(root.right, array);
}

方法二：不用收集所有節點，設置一個計數器，在中序走訪的過程中，累加訪問過的節點數，當計數器的值等於 k 時，回傳該節點。

function kthNode2(root, k) {
  let index = 0;
  const _kthNode = (root, k) => {
    if (root) {
      let node = _kthNode(root.left, k);
      if (node !== null) {
        return node;
      }
      index++;
      if (index === k) {
        return root;
      }
      node = _kthNode(root.right, k);
      if (node !== null) {
        return node;
      }
    }
    return null;
  };
  return _kthNode(root, k);
}

小結

我們今天已經看完了深度優先走訪的實作，基本上深度優先走訪的實作都是透過遞迴或者 stack 來實現的，而且遞迴的實現方式比較簡單，所以通常只需要掌握遞迴的實現方式就可以了。明天我們要繼續來看到廣度優先走訪，並且還要來實作如何在終端中 print 出一棵樹。

參考資料

• 《JavaScript 算法：基本原理與代碼實現》