本文同步更新於個人網站中,有更好的排版和程式碼區塊 highlighting 支援。
昨天我們已經介紹了深度優先走訪的三種方式,今天我們來介紹廣度優先走訪,並且實作一下如何在控制台或終端 print 出一棵樹的結構。
廣度優先走訪又叫作層序走訪(Level Order Traversal),比如我們要按照層次輸出一棵樹的所有節點的組合(LeetCode 107),又比如求一棵樹的最左節點(LeetCode 513),這些都是廣度優先走訪的應用。其走訪樹結構如圖所示:
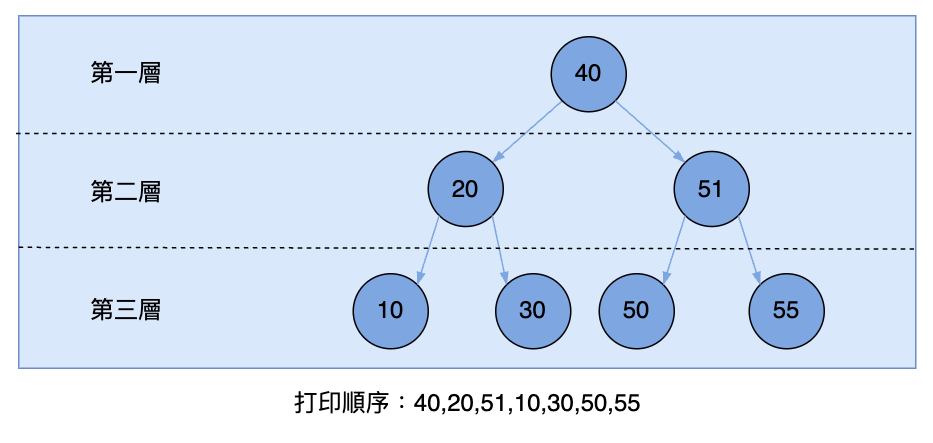
廣度優先走訪比較好實作,我們參考前序走訪的過程,先放入根節點,然後跑迴圈,在迴圈中把根節點拿出來打印,然後再依次放入左子節點和右子節點,再回到迴圈中,把左子節點拿出來打印.....這個過程需要先進先出,所以用 queue 來實作。
levelOrder(callback) {
const queue = [];
let node = this.root;
node && queue.push(node);
while (queue.length) {
node = queue.shift();
callback(node);
if (node.left) {
queue.push(node.left);
}
if (node.right) {
queue.push(node.right);
}
}
}
要檢測輸入的順序是否正確,最佳的方法是圖形化地將樹打印出來。要 print 出一棵樹與樹的走訪息息相關,接下來我們來看兩種常用的打印方式。
這是一種常見的目錄 tree 的打印方式,先打印出根節點,然後打印出左右子樹,所以我們需要用到前序走訪。具體實作如下:
toString() {
let out = [];
this.preOrder((node) => {
const parent = node.parent;
if (parent) {
const isRight = parent.right === node;
out.push(parent.prefix + (isRight ? '└── ' : '├── ') + node.data);
const indent = parent.prefix + (isRight ? ' ' : '│ ');
node.prefix = indent;
} else {
node.prefix = ' ';
out.push('└──' + node.data);
}
});
return out.join('\n');
}
const tree = new Tree();
tree.insert(1);
tree.insert(2);
tree.insert(3);
tree.insert(4);
tree.insert(5);
tree.insert(6);
tree.insert(7);
tree.insert(8);
console.log(tree.toString());
執行上面的程式碼後,打印出來的結構如下:
└──1
├── 2
│ ├── 5
│ └── 7
└── 3
├── 4
└── 6
├── 8
在 1 所對應的垂直線上,有兩條相交的水平線,上面代表左節點,下面是右節點,其他的節點也是這樣。
縱向打印說實話還是沒有非常直觀,需要我們去想象一下樹的結構。如果我們打印的樹是這種樣子,是不是就更好理解了呢?
50
──────── ────────
30 70
我們首先從分層開始,這要借助 queue 與一個 0 作為目前層級的結束標記。具體實作如下:
printNodeByLevel(callback) {
const queue = [];
let node = this.root;
if (node) {
queue.push(node);
queue.push(0);
}
while (queue.length > 0) {
node = queue.shift();
if (node) {
callback(node);
if (node.left) {
queue.push(node.left);
}
if (node.right) {
queue.push(node.right);
}
} else if (queue.length > 0) {
callback(node); // output 0
queue.push(0);
}
}
callback(0);
}
toString() {
const allLevels = [];
let currLevel = [];
this.printNodeByLevel((node) => {
if (node === 0) { // 目前層級結束
allLevels.push(currLevel);
currLevel = [];
} else {
currLevel.push(node.data); // 收集目前層級的所有節點
}
});
return allLevels.map((level) => level.join(',')).join('\n');
}
const tree = new Tree();
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11].forEach((num) => tree.insert(num));
console.log(tree.toString());
執行上面的程式碼後,會看到如下的結果:
1
2,3
5,7,4,6
9,11,8,10
這樣第一步就算大功告成了,接下來我們需要在數字間新增一些空白和連線,讓它看起來更像一棵樹。假設樹只有根與左右子樹,那麼樹分為兩層。第一層根節點左邊的空白應該要是左子樹值的長度,而根節點右邊只需要給它一個換行符就行了。第二層裡,左子樹已經在最左邊,所以左邊不需要填充空白,中間則填上與根節點相同長度的空白,右子樹已經在最右邊,所以不需要再放東西了。
具體看起來會像這樣:
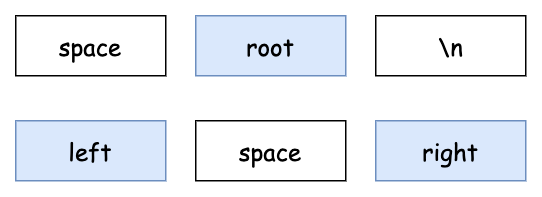
如果不止兩層,我們就要考慮 left 是否有子節點,這個子節點的左邊有多少空白,left 本身又需要多少空白,但這樣計算起來非常複雜,而且每個節點長度不一樣,無法規律的計算某一層的某一個位置相對左側需要多少距離。因此我們需要統一 data 的長度。想像我們的樹是一座金字塔,每個磚頭的長度是 4,如果這些磚頭可能放節點的 data,此時長度不夠就用 “_” 補在兩旁,如果放的是空白,那就要確保是長度為 4 的空白。如下圖:
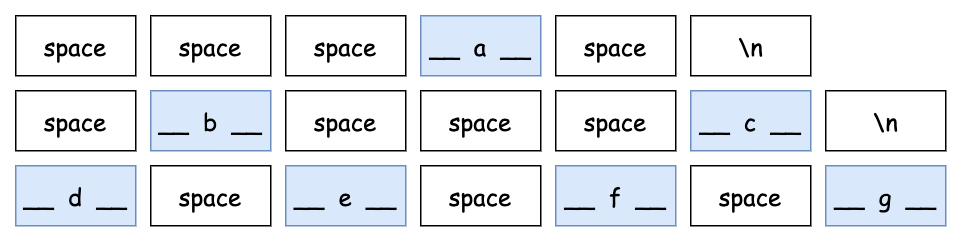
然後我們再把一些空白全部換成底線,例如 a 兩側的 space,如下:
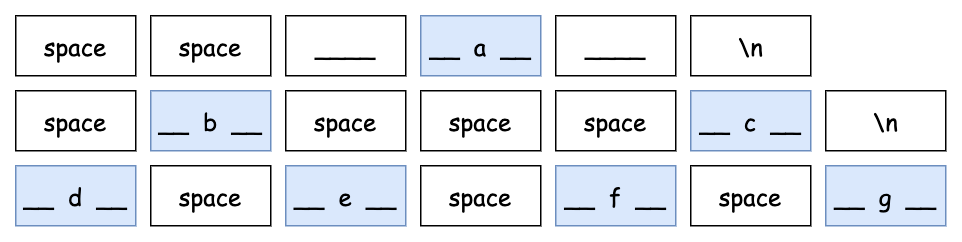
此時我們就可以認出 b、c 是 a 的子節點,但是其他結構還是不太明顯,我們可以在每層間再墊高一層,加上一些斜線,金字塔就成形了,如下:
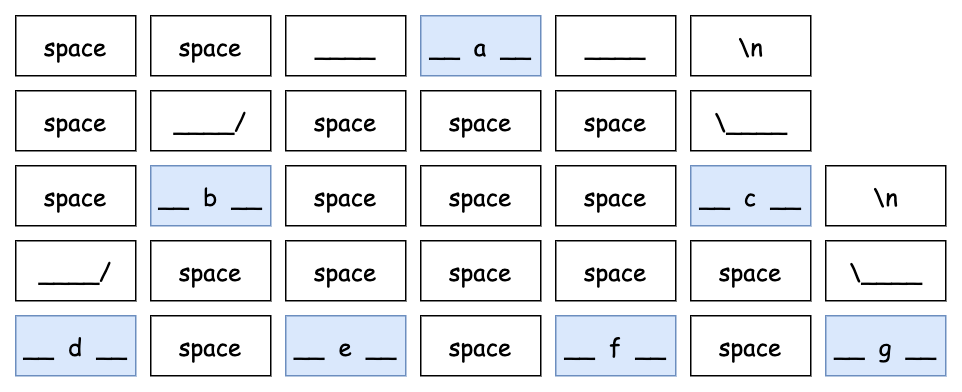
要實現這樣的效果,我們需要進行兩次樹的走訪,第一次是廣度優先走訪,得到每一層的節點;第二次是中序走訪,計算每個節點的索引值,也就是它在陣列中的位置。有了索引值就可以計算出它到最左邊的距離。
現在來重寫一下 toString 方法:
toString(displayData) {
// 輔助方法,讓資料置中對齊
const brickLen = 6;
const SW = ' ';
const LINE = '_';
displayData =
displayData ||
function (node) {
const { data, left, right } = node;
let s = '(' + data + ')';
const isLeaf = !left && !right;
const fillChar = isLeaf ? SW : LINE;
const paddingLength = brickLen - s.length;
for (let i = 0; i < paddingLength; i++) {
if (i % 2 === 0) {
s = s.padEnd(s.length + 1, fillChar);
} else {
s = s.padStart(s.length + 1, fillChar);
}
}
return s;
};
// 建立 4 個字元的空白或底線
function createPadding(s, n = brickLen) {
let ret = '';
for (let i = 0; i < n; i++) {
ret += s;
}
return ret;
}
// ==== 以下是主要的 toString 方法 ====
// 新增索引值
let index = 0;
this.inOrder((node) => {
node.index = index++;
});
// 取得每一層的節點
const allLevels = [];
let currLevel = [];
this.printNodeByLevel((node) => {
if (node === 0) {
allLevels.push(currLevel);
currLevel = [];
} else {
currLevel.push(node);
}
});
// bricks 中有 data 的層級,branches 只是用來放斜線的層級,兩個都是二維陣列
const bricks = [];
const branches = [];
for (let i = 0; i < allLevels.length; i++) {
if (!bricks[i]) {
bricks[i] = [];
branches[i] = [];
}
let cbrick = bricks[i];
let cbranch = branches[i];
let level = allLevels[i];
while (level.length > 0) {
let el = level.shift();
let j = el.index;
// 確保 cbirck[j] 與 cbranch[j] 等長
cbrick[j] = displayData(el);
cbranch[j] = createPadding(SW, cbrick[j].length);
if (el.parent) {
let pbrick = bricks[i - 1];
let pbranch = branches[i - 1];
let pindex = el.parent.index;
if (el === el.parent.left) {
// 左子樹
for (let k = j + 1; k < pindex; k++) {
pbrick[k] = createPadding(LINE);
}
for (let k = j + 1; k < pindex; k++) {
pbranch[k] = createPadding(SW);
}
pbranch[j] = createPadding(SW, brickLen - 1) + '/';
} else {
// 右子樹
for (let k = pindex + 1; k < j; k++) {
pbrick[k] = createPadding(LINE);
}
for (let k = pindex + 1; k < j; k++) {
pbranch[k] = createPadding(SW);
}
pbranch[j] = '\\' + createPadding(SW, brickLen - 1);
}
}
j--;
inner: while (j > -1) {
// 添加空白
if (cbrick[j] == null) {
cbrick[j] = createPadding(SW);
cbranch[j] = createPadding(SW);
} else {
break inner;
}
j--;
}
}
}
return bricks
.map((row, i) => {
return row.join('') + '\n' + branches[i].join('');
})
.join('\n');
}
然後在控制台中就可以 print 出整棵樹了:
_______(1)________
/ \
_______(2)__ _(3)________
/ \ / \
_(5)__ (7) (4) _(6)________
/ \ / \
(9) (11) (8) _(10)_
/
(12)
要在控制台裡實際印出一棵樹在實作上比較繁瑣,需要用上廣度與深度兩種走訪方式,可以當作是一個練習,在控制台畫畫圖也是一種樂趣。
到今天為止已經介紹了樹的基本概念和走訪方式,明天我會介紹一個樹的應用:二元搜尋樹。二元搜尋樹是一個非常經典的資料結構,幾乎所有教學資源在介紹二元樹的同時都會介紹二元搜尋樹,因為它的應用非常廣泛,而且實作也不難,至少跟 print 出一棵樹相比起來。
