Hi 大家好，在分享了一些和Adjacency list有關的概念和題目後，今天要分享的是Matrix。這個題型在coding interview也是很熱門的題型。我們直接來看題目邊講解他的一些概念吧。

Leetcode 200. Number of Islands

題目敘述：有一個二維的陣列，上面只會有'0'和'1'，'0'代表的是水域；'1'代表的是陸地。定義：島嶼是一片陸地相連並且四周被水域包圍。找出在這個二維陣列上有幾座島嶼。

Example:

Input: grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
Output: 3

解釋：這就是一題十分典型的matrix問題。所謂的matrix指的是將節點以某個符號表示（這題以'1'表示），並且所有相鄰的節點是上下左右相連的，而其他非節點的部分則以另一個符號表示（這題以'0'表示）。
將上面的example中的節點視覺化（雖然有點醜XD）的話就長這樣：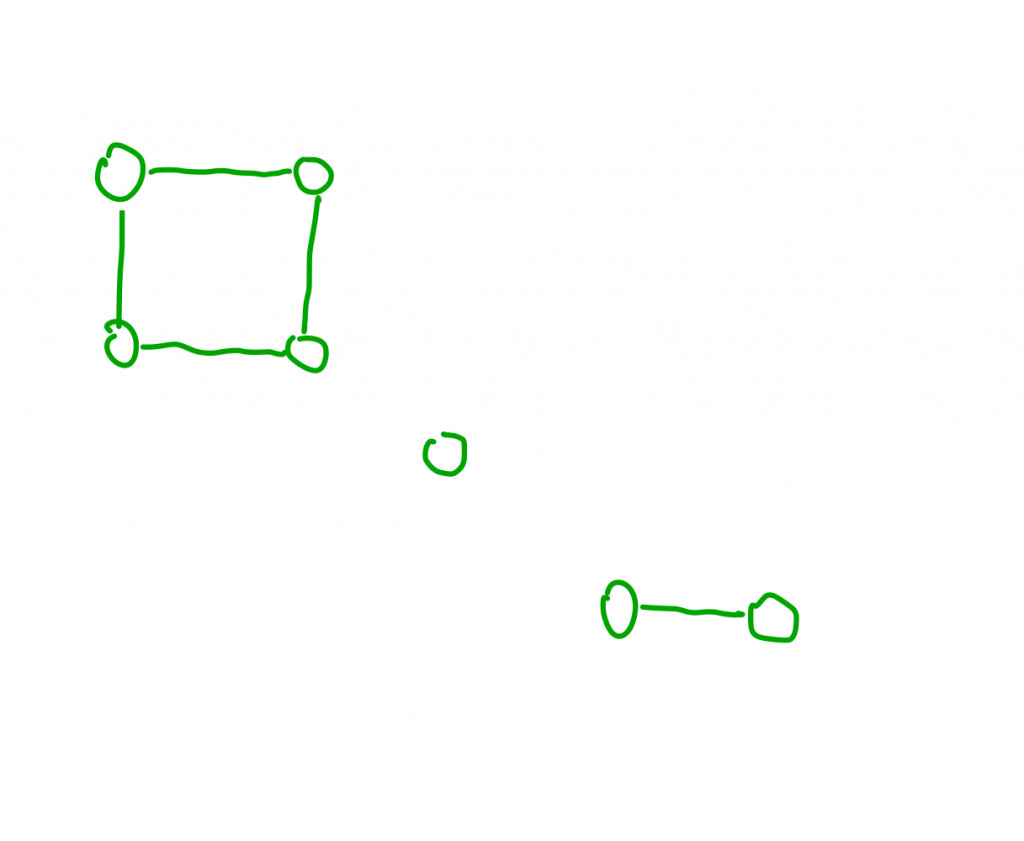

分析：我們需要去拜訪這些節點，並且每一次都是只拜訪一座島嶼他所擁有的節點。拜訪完這些節點就確定有一座島嶼，並且累加有幾座島嶼。題目已經說明島嶼是相連的陸地（節點）所形成，根據前面的分析，我們要一次計算一條相連的「路徑」，這種拜訪就是DFS。

DFS: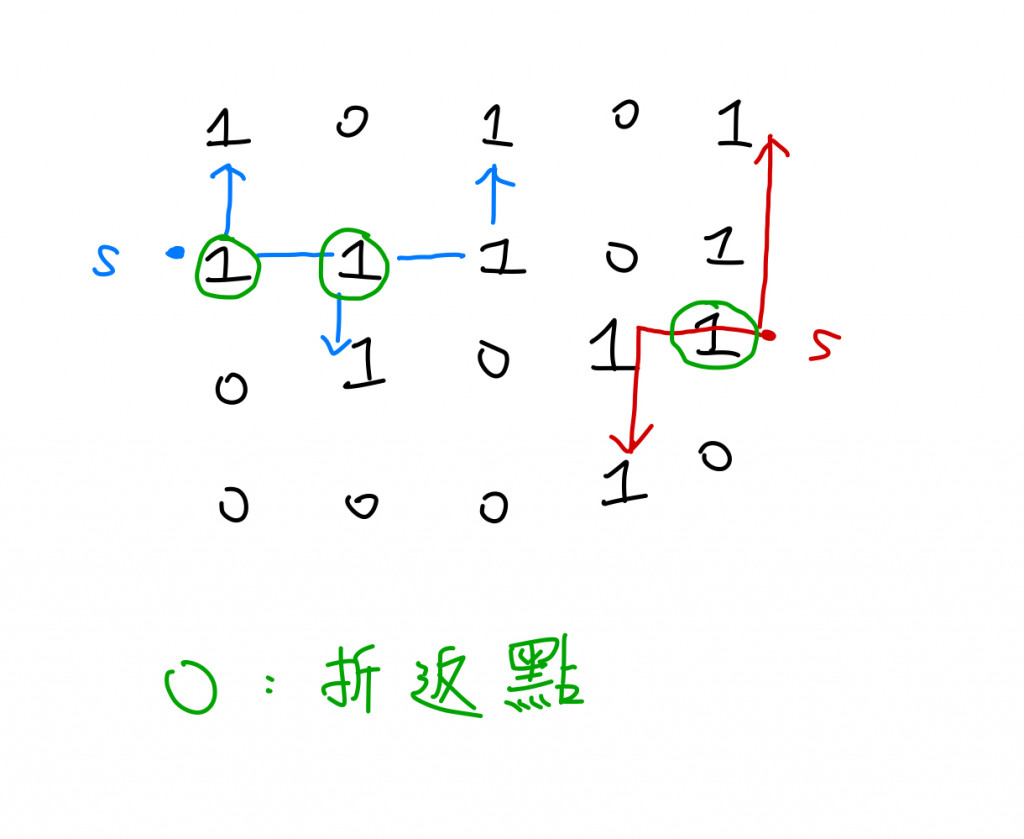

DFS的特性就是每次都只會拜訪完一條路徑，之後回到折返點再去拜訪其他相連的路徑，所以需要一個可以去紀錄他已經拜訪過哪些節點的set，以免會造成無限迴圈。

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        visit = set()
        ROW, COL = len(grid), len(grid[0])

        def dfs(r, c):
            if r < 0 or r == ROW or c < 0 or c == COL or grid[r][c] == "0":
                return
            if (r, c) in visit:
                return
            
            visit.add((r, c))

            dfs(r + 1, c)
            dfs(r - 1, c)
            dfs(r, c + 1)
            dfs(r, c - 1)
        
        count = 0
        for i in range(ROW):
            for j in range(COL):
                if (i, j) not in visit and grid[i][j] != "0":
                    count += 1
                    dfs(i, j)
        
        return count

注意：在dfs函數中的第一個if是針對邊界以及無法通行的地方所做的過濾。

Leetcode 695. Max Area of Island

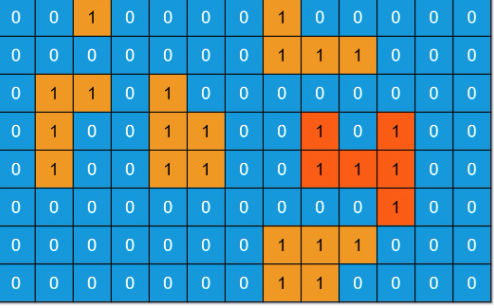
題目敘述：這次要找出哪一座島嶼擁有最大的面積，每一片陸地以1代表，並且面積都是1單位；水域則以0代表。

分析：這類型的問題主要的模板不會有太大的變動，主要修改的地方就是dfs的計算方式。因為每一個代表陸地的cell都是1單位，所以每次從這塊陸地出發去拜訪四周的陸地時會是（1 + 和他相連的其他路徑上的陸地的面積）

class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        maxArea = 0
        visit = set()
        ROW, COL = len(grid), len(grid[0])
        
        def dfs(r, c):
            if r < 0 or r == ROW or c < 0 or c == COL or grid[r][c] == 0:
                return 0
            if (r, c) in visit:
                return 0

            visit.add((r, c))
            area = 1
            area += dfs(r - 1, c)
            area += dfs(r + 1, c)
            area += dfs(r, c - 1)
            area += dfs(r, c + 1)

            return area
        
        for i in range(ROW):
            for j in range(COL):
                if (i, j) not in visit and grid[i][j] == 1:
                    maxArea = max(maxArea, dfs(i, j))
        
        return maxArea

明天會分享BFS在Matrix上的應用，謝謝大家觀看本文。