Hi 大家好，今天來分享BFS在Matrix的應用。BFS如果應用在像binary tree上的話，我們每一次都會一次拜訪到同一個Level上的所有的所有節點。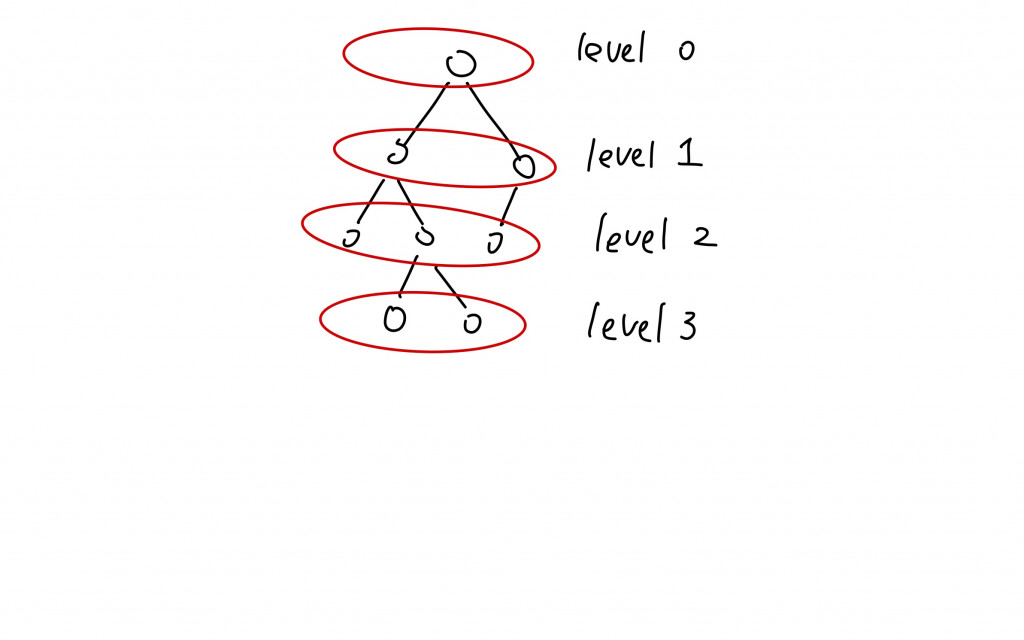

如圖所示，所以也叫做level order traversal。

一樣地，把這個概念應用在matrix上的話，他也是會一層一層去拜訪那些根據規則相連的節點。
假設1代表節點並且會和上下左右的節點相連，那麼在這個matrix上從左上進行BFS會長這樣：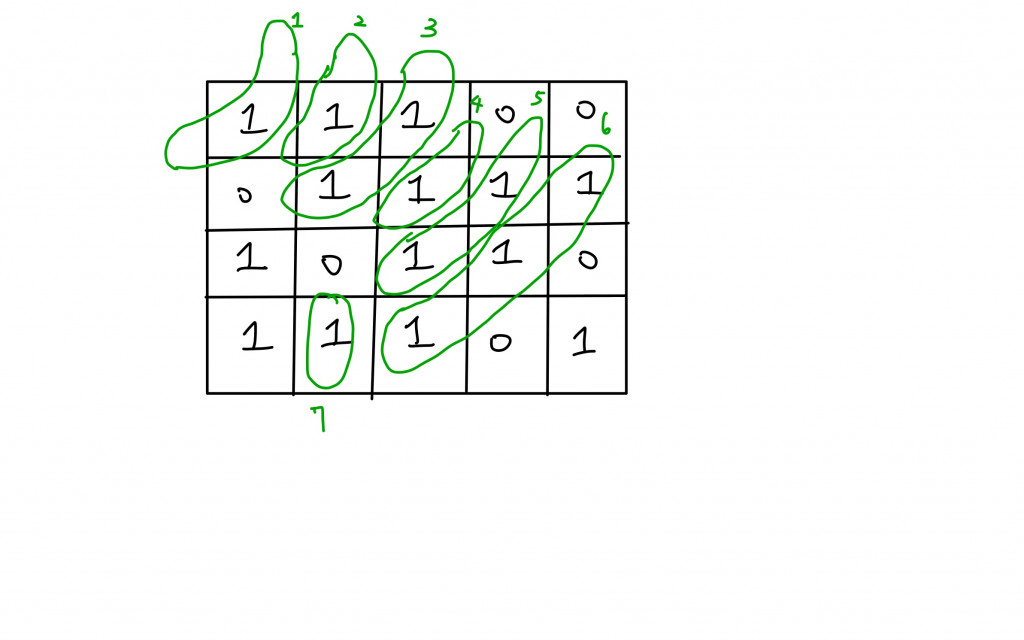

以綠色橢圓圈起來並且標示數字代表是第幾次（層）被擺訪到的。

BFS在matrix上適合解決從某個節點到另一個節點的最短路徑的問題或是同時有複數個起點的問題。

Leetcode 994. Rotting Oranges

題目敘述：有一個二維的M * N的陣列，裡面有數字0, 1, 2分別代表：
0: 空格
1: 新鮮的橘子
2: 腐敗的橘子
腐敗的橘子每分鐘會讓他四方和他相接的新鮮橘子也腐敗，請問要花多少分鐘才能讓所有橘子都腐敗。如果不行就回傳-1。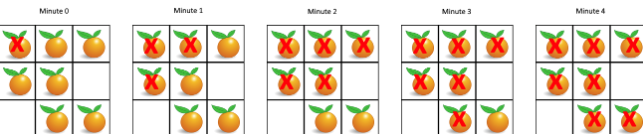

(圖源: leetcode）

分析：
根據題意，我們有兩種節點，1和2，2只能往1走。並且因為2可能會分散在matrix的各個位置，我們要同時計算他們會往哪邊走，因為他們會同時影響他們自己的四周，代表有可能遇到複數個起點的情況。這時候利用BFS把這些起點都當作同一層就能解決問題。
另外，我們要知道總共有幾顆橘子（不論新鮮與否），還要有個專們紀錄哪些橘子已經腐敗的set。當BFS結束後，我們比較腐敗的橘子個數是否和橘子總數一樣。

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        total = 0
        ROW, COL = len(grid), len(grid[0])
        rotten = deque()
        visit = set()
        time = 0

        for i in range(ROW):
            for j in range(COL):
                if grid[i][j] == 2:
                    rotten.append((i, j))
                    visit.add((i, j))
                    total += 1
                elif grid[i][j] == 1:
                    total += 1
        
        while rotten and len(visit) < total:
            for i in range(len(rotten)):
                (r, c) = rotten.popleft()
                for dr, dc in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
                    if (0 <= r + dr < ROW and
                        0 <= c + dc < COL and
                        grid[r + dr][c + dc] == 1 and
                        (r + dr, c + dc) not in visit):
                        visit.add((r + dr, c + dc))
                        rotten.append((r + dr, c + dc))
            
            time += 1

        return time if len(visit) == total else -1

Leetcode 1091. Shortest Path in Binary Matrix

題目敘述：形狀為正方形的matrix中只有0和1，0代表節點並且可以和「八方」也是0的節點相連。找出從左上到達右下的最短路徑。找不到就回傳-1。

Example: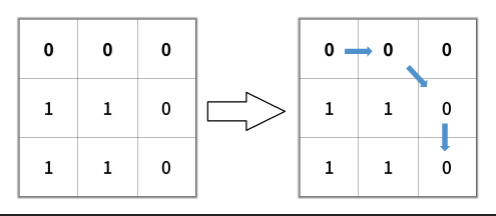

(圖源：leetcode)

Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

分析：根據範例，我們從左上的起點開始計算到達右下時總共有多少個0。我們在計算時需要用到一個紀錄已經拜訪過哪些節點的set，這樣可以避免重複拜訪到節點，我們只需要「第一次拜訪到這個節點」時已經累積了多少次0，下一次拜訪到這個節點時累積的0的次數一定比較多，既然題目是要求最短距離自然要忽略。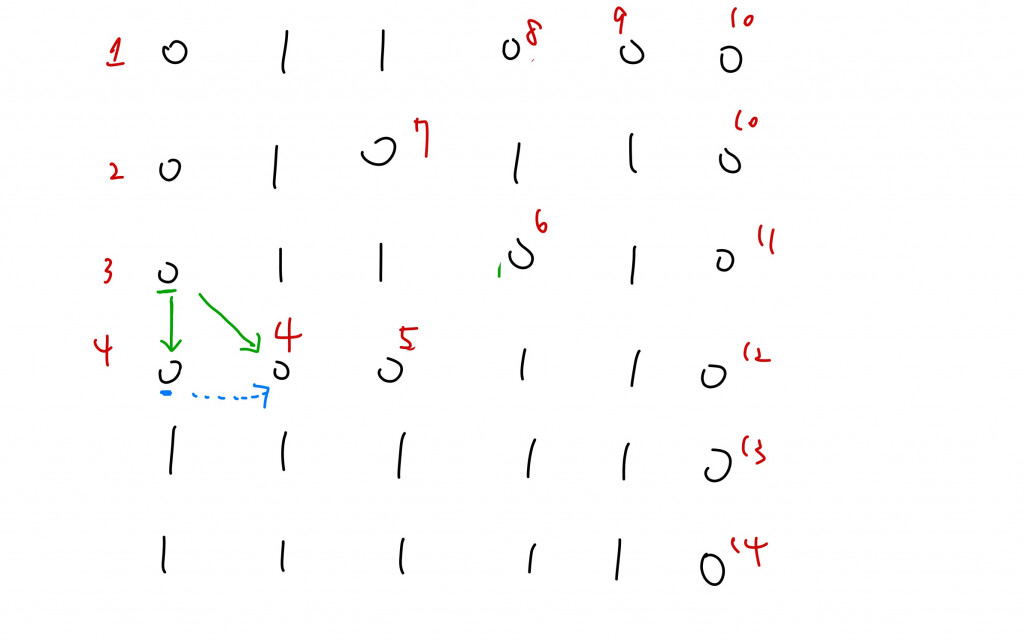

從圖中可以看到被綠色標記的節點，他可以讓下一層也兩個節點（綠色箭頭），並且它們累積的0都是"3 + 1"，並且這兩個節點都已經被拜訪過了，當BFS到下一層時就會有這兩個節點，其中藍色標記的節點會想往上和往右走，但會發現都已被標記而忽略。

class Solution:
    def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        if grid[0][0] == 1:
            return -1
        N = len(grid)

        q = deque()
        q.append((0, 0, 1))
        visit = set()
        # visit.add((0, 0))

        while q:
            for i in range(len(q)):
                (r, c, d) = q.popleft()

                if r == N - 1 and c == N - 1:
                    return d

                for dr, dc in [[1, 0], [0, 1], [-1, 0], [0, -1], [1, -1], [-1, 1], [1, 1], [-1, -1]]:
                    if (0 <= r + dr < N and
                        0 <= c + dc < N and
                        grid[r + dr][c + dc] == 0 and
                        (r + dr, c + dc) not in visit):
                        visit.add((r + dr, c + dc,))
                        q.append((r + dr, c + dc, d + 1))
        
        return -1

這樣Graph的基礎篇就大致介紹完了，之後預計會介紹Graph中比較進階的主題。